|
||||||||||||||||||||||||||||||||||||||||
![]()
|
RÉSIDUS QUADRATIQUES et Réciprocité quadratique Une
loi mettant en scène des congruences
sur des nombres carrés.
Un peu curieuse a priori. C'est Gauss
qui l'a introduite. Elle s'avère un instrument très utile en théorie des
nombres. |
Anglais: Quadratic
forms and quadratic reciprocity law
|
|
||
|
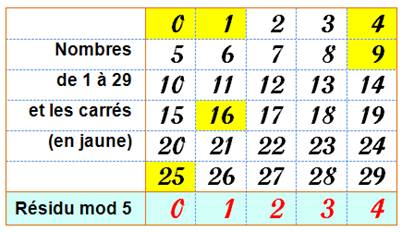
En jaune les carrés et leur position sur les colonnes de
même résidu modulo 5. Ainsi
5² = 25 = 0 mod 5 4² = 16 = 1 mod 5 etc. Façon
un peu sophistiquée de dire que 5² est divisible par 5 ou que 4² donne un
reste de 1 par la même division. |
On cherche à classer les carrés selon le reste de la division par n.
Les nombres 4 et 9 ont même résidu en mod 5. |
|
Rappel des valeurs possibles des restes de la division par m (le
mod) d'un carré
|
Exemple:
un carré divisé par 8 ne peut donner que le reste 0, 1 ou 4.
|
|
|
|
|
Il s'agit de chercher si l'équation
x² La
loi de la réciprocité quadratique Elle dit que: x²
Exemple avec 5 et 11:
x²
Cette loi permet de contourner
certains problèmes en les ramenant à des questions plus simples à résoudre. |
|
|
|
|
|
The question remains as to
whether x² The quadratic reciprocity law
states that if p and q are distinct odd primes, the two congruencies x² |
|
![]()
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/ARITHMET/ResiQuad.htm
|
![]()