|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
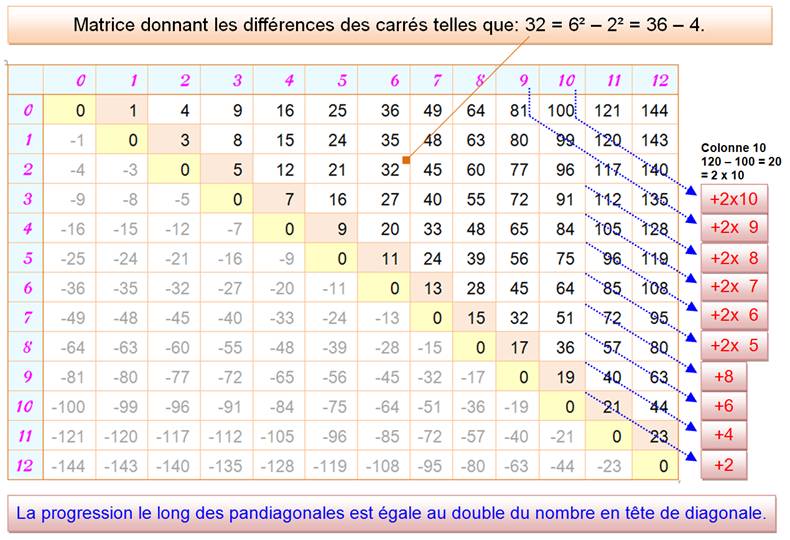
ÉCART ENTRE CARRÉS, observations et formulations N = n² – m² Toutes
les propriétés résumées en un seul tableau. |
|
|
|
|
|
|
|
|
||
|
|
Tout nombre impair est
la différence des carrés de deux nombres consécutifs: E = m² – (m – 1)² = m + (m – 1) 102 – 92
= 10 + 9 = 19 10002 – 9992
= 1000 + 999 = 1999 => 999² = 1 000 000
– 1 999 = 998 001 |
|
|
|
||
|
|
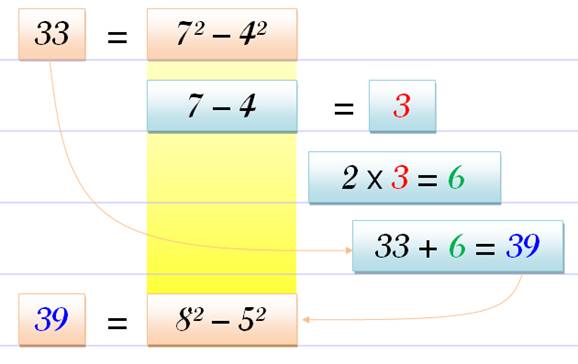
En effet, soit les
deux nombres: m et m – k: = m² – m²
+ 2mk – k² = k (2m – k) Si k = 1 (nombres consécutifs; première pandiagonale): E = 2m – 1, nombre impair. Si k > 1 (autres pandiagonales) E = k (2m – k) Divisible par k
qui n'est pas 1, donc nombre composé. |
|
|
|
||
|
|
A = m² B = (m –
k)² = m² - 2mk + k² C = (m –
1)² = m² - 2m + 1 D = (m – k – 1)² = m² -
2mk – 2m + k² + 2k + 1 E = (A – B) – (C – D) = 2k L'écart entre deux
nombres d'une pandiagonale est le double de la distance (k) entre les deux
nombres. |
|
|
|
|
|
|
|
|
|
||
|
9² – 2² = 77 9² – 5² = 56 Écart = 21
m = 9, k = 7 et h = 4 = 3 x 7 = 21 |
A = m² B = (m –
k)² = m² - 2mk + k² C = m² D = (m – h)² = m² - 2mh + h² E = (A – B) – (C – D) = h² – k² + 2m(k – h) = (h – k)(h + k) – 2m(h – k) = (h – k)(h + k –
2m) |
|
|
|
||
|
9² – 3² = 72 6² – 3² = 27 Écart = 45
m = 9, k = 6 et j = 3 |
A = m² B = (m –
k)² = m² - 2mk + k² C = (m –
j)² = m² - 2mj + j² D = (m – k)² = m² - 2mk + k² E = (A – B) – (C – D) = j (2m –j) |
|
|
|
||
|
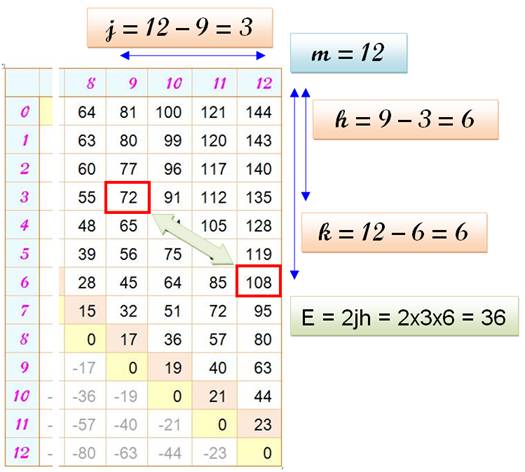
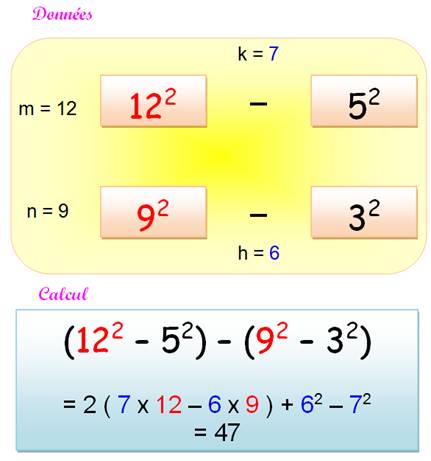
12² – 5² = 119 9² – 3²
= 72 Écart
= 47
m = 12,
k = 7, j = 3 et h = 6 = (-1) (-11) + 36 = 47 |
A = m² B = (m –
k)² = m² - 2mk + k² C = (m –
j)² = m² - 2mj + j² D = (m – j
- h)² = m² + h² + j²- 2mj – 2mh+ 2jh E = (A –
B) – (C – D) = h² – k² + 2m (k – h) + 2jh = (h – k)(h + k – 2m) + 2jh = Ecolonne
+ 2jh |
|
|
|
||
|
12² – 6² = 108 9² – 3²
= 72 Écart
= 36
m = 12, k = 6, j = 3 et h = 6 |
Comme précédemment, mais avec h = k: E = (A – B) – (C – D) = (h –
k)(h + k – 2m) + 2jh = 0 + 2jh = 2jh Notez que
cet écart est indépendant de m. |
|
|
|
||
|
ÉCART Nombres
quelconques: l'écart entre les carrés de deux nombres est
égal au produit de leur somme et de leur différence. Deux
nombres consécutifs: l'écart entre leurs carrés est un
nombre impair. E = m² – (m – 1)² = m + (m – 1) = 2m – 1 PROGRESSION Nombres
sur une pandiagonale: (m² – k²) et (n² – k²): l'écart entre
ces deux valeurs est indépendante de m et de n; elle est égale au double du
produit de la différence j = m – n par le numéro de la pandiagonale k (ou h).
E = (m – k)² –
(n – k)² = 2 (m –
n) k Nombres quelconques: E = (m²– (m-k)²) – (n² – (n-h)²) = (h – k)(h + k – 2m) + 2(m – n) h = 2(km – hn) + h²- k² Exemple
|
Voir Résumé des propriétés des
carrés
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/P100a500/DifcarTB.htm |
![]()