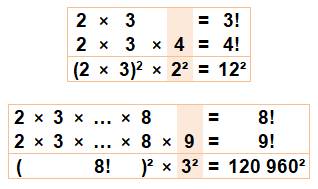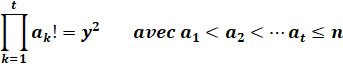|
||||||||||||||||||||||||||||||||
![]()
|
Produits de FACTORIELLES = Carrés
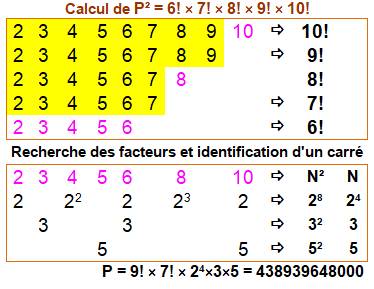
Quels sont les produits de
factorielles qui sont des carrés ? Exemple avec le produit de trois factorielles consécutives. Le tableau
montre la construction du carré final. En jaune un carré naturel et en rose un carré plus inattendu: |
Retour à l'introduction
sur les factorielles / Brève
N° 499
|
|
||||
|
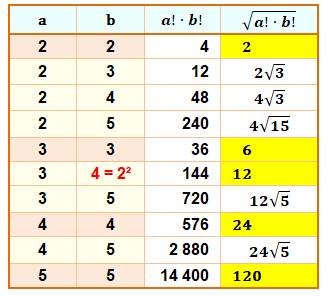
Pour
toutes les possibilités de deux facteurs a et b de 2 à 5, le produit des
factorielles de ces nombres forme un nombre carré:
Dans ce dernier cas, on a: Il suffit, pour que ce produit soit un carré, que
n + 1 soit un carré. |
|
|||
|
Exemples avec nombres consécutifs
dont le second est un carré 3! x 4! = 3!² x 4 = 3!² x 2² = (3! x 2)² 8! x 9! = 8!² x 9 = 8!² x 3² = (8! x 3)² |
|
|||
|
Dans le cas général Avec deux nombres "éloignés", le nombre
b présente des facteurs en plus (couleur). Il s'agit d'une factorielle
tronquée. Comme la factorielle
complète, la factorielle tronquée n'est jamais un carré. |
|
|||
|
Bilan Le tableau montre les produits de deux
factorielles égales à un carré. Tous les couples (a, b), avec b = a + 1 et b est
un carré, sont présents. Aucun autre couple de deux nombres ne produit un
carré. |
|
|||
|
|
||
|
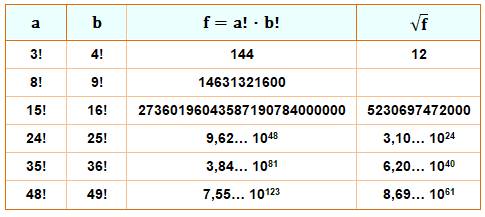
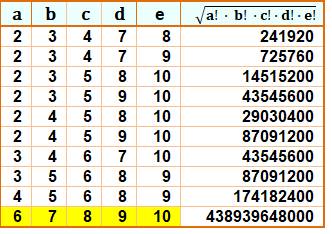
Exemple de calcul avec trois
facteurs 3! x 5! x
6! = (5!)² x 2x3x6 = 720²
Tableau pour toutes les
possibilités avec {a, b, c} jusqu'à 50 Seuls
quatre cas pour un produit inférieur à un million dont les cas remarquable en
{4, 5, 6}. |
|
|
|
|
|||
|
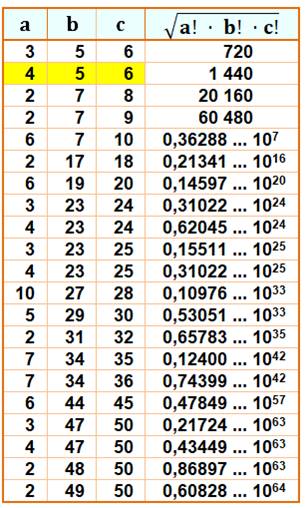
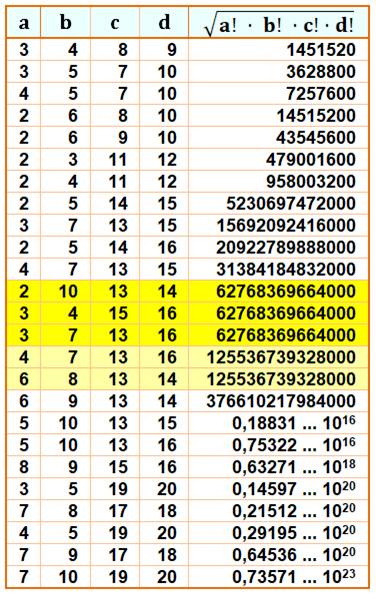
Exemple de calcul avec trois
facteurs 3! x 5! x
6! = (5!)² x 2x3x6 = 720²
Tableau pour toutes les
possibilités avec {a, b, c, d} jusqu'à 20 On note
en jaune, des produits identiques pour des facteurs différents |
|
||
|
Ce cas est intéressant et nous le connaissons
déjà. Il s'agit de deux couples de factorielles
consécutives dont le plus grand nombre est un carré: |
|
||
|
Avec ce cas, dont le produit est identique au
précédent, il faut identifier le carré:
Tous les facteurs ont une puissance paire. Le
produit est un carré. |
|
||
|
Quant au troisième produit identique, le même
type de calcul s'applique pour trouver sa racine carrée. Notez que les deux produits P, hors 13!, sont
identiques: |
|
||
![]()
527 et
produits de factorielles
|
Rappel: théorème d'Erdös et
Selfridge (1975) Une factorielle tronquée n'est jamais une
puissance parfaite. Produit de factorielles Pour tout entier n, on peut trouver r entiers a1
< a2 < … < ar avec ar =
n, tels que le produit de leurs factorielles soit un carré. On a démontré que: Le nombre 527 est le plus petit entier qui requiert effectivement r =
6. Les
nombres remarquables – François Le Lionnais – 1983 Démontré
par Erdös et Selfridge |
|
Commentaires: OUPS ! Une vérification expérimentale ne me conduit pas à vérifier ce
théorème en l'état. Je pense qu'il faut dire: Pour tout entier n
composé supérieur à 8, on peut trouver r
entiers … Quelques
solutions minimales [8, 7, 4, 3, 2,
1, 3], 241920 [9, 7, 4, 3, 2,
1, 5], 725760 [10, 8, 5, 3, 2,
1, 9], 14515200 [11]
Aucune solution pour ce nombre premier [12, 11, 6, 5,
2, 1, 16], 57480192000 [13] [14, 13, 7, 6,
2, 1, 14],
62768369664000 [15, 14, 6, 3,
2, 1, 21], 31384184832000 [16, 14, 6, 3,
2, 1, 36], 125536739328000
[18, 17, 4, 3,
2, 1, 35], 25609494822912000 [19] [20, 19, 6, 4,
3, 1, 33],
175168944588718080000 [21, 19, 7, 3,
2, 1, 76],
613091306060513280000 [22, 19, 11, 6,
3, 1, 71], 4855683143999265177600000 Toutes ces solutions utilisent seulement 5 factorielles. Erdös et Graham donnent les solutions particulières indiquées dans
l'encadré blanc. Toutes avec seulement 5 factorielles. C'est le nombre 527 qui est le premier à nécessiter 6 factorielles. |
|
Texte de Erdös et Graham (traduction de la page
338) Nous étudions l'équation:
Notamment dans le cas où on impose n, la valeur du plus grand ak
et en utilisant le minimum de factorielles. Il se trouve qu'à chaque augmentation de t (la quantité de factorielles
utilisées), l'ensemble des valeurs de n solutions de l'équation augmente
considérablement jusqu'à stagner pour t = 6 Texte original
|
![]()
|
Retour
|
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
![]()