NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/10/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	LOGIQUE
Débutants Logique	Intelligence artificielle			Glossaire Algorithme
INDEX Logique	Introduction	Algorithme débutant	Algorithmes	Programmation
	Collège	Algorithmes TOP 15	Robots
		Sommaire de cette page >>> Approche >>> Répétition >>> Pour simplifier >>> Bilan >>> S'exercer avec Scratch >>> Exemple d'un algorithme simple >>> Algorithme d'entraînement

ALGORITHMES

Totalement débutant

Explications et exemples pour bien comprendre cette notion.

APPROCHE
Vous allez vous laver les mains! Vous pratiquer un algorithme sans savoir que cela s'appelle comme cela. Imaginez que vous rencontrez quelqu'un à qui vous devez tout expliquer, pas à pas, alors vous décrivez l'algorithme de lavage de mains. Le lavage de mains est décrit en indiquant sept opérations simples. On utilise le mot "instructions". Un algorithme est une suite d'instructions. C'est une recette, une manière de faire, décrite pas à pas. L'avantage est que n'importe qui peut se servir de cette description. Elle est valable pour moi, ma sœur, mon copain, mon correspondant au Canada … Attention: l'important et ne pas oublier une instruction dans la description. 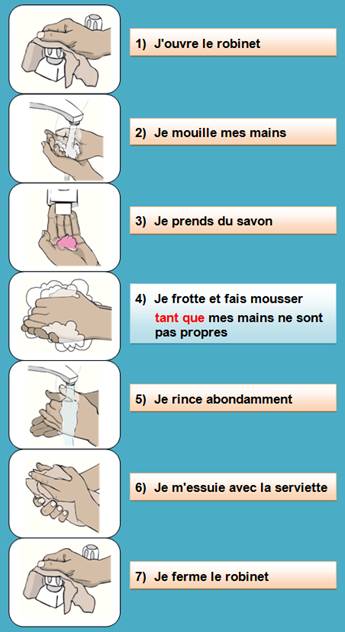Note: dans le cadre des économies d'eau, il est conseillé de fermer le robinet avant de s'essuyer... me dit très justement Valery d'A.
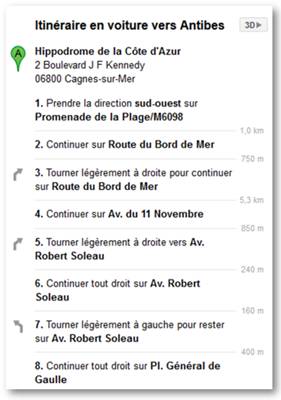
Exemple avec l'indication d'un itinéraire Pour allez de ma maison à mon bureau: Monter dans la voiture; Démarrer et avancer; Tourner à la première à droite; S'arrêter au feu et attendre le vert; Avancer jusqu'au 3^e carrefour; Prendre la 2^e à droite; Etc. La liste des instructions pour aller d'un point à un autre est une sorte d'algorithme. Ci-contre un exemple avec Google-Map.

Récréation

Choisir un chiffre C de 1 à 9, le multiplier par 37, ajouter ce nombre à lui-même, encore une fois. Surprenant non?

Exemple: je choisis 7. Alors, 7 x 37 = 259; 259 + 259 = 518; 518 + 259 = 777

Lorsque je choisis un chiffre C, je donne une valeur à C, j'affecte un chiffre à C.

Répétition
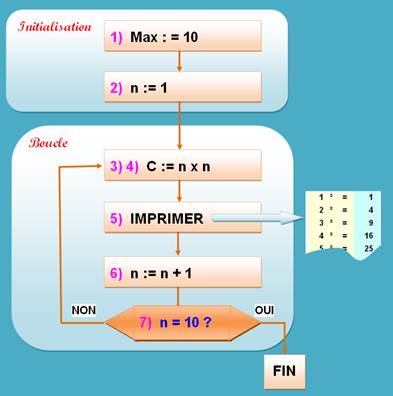
Quel est l'intérêt d'un l'algorithme? C'est de pouvoir le porter (l'implanter) dans un ordinateur ou une calculette pour faire des travaux: fastidieux répétitifs, compliqués Voyons cela pas à pas sur un exemple de calcul de carrés.	Calcul des dix premiers carrés C = n²
J'indique combien de carrés je désire dans une mémoire que j'appelle "Max". Si j'en veux 100, il me suffit de mettre 100 à la place de 10 comme ici.	1) Mettre 10 dans la variable Max;
Le nombre à mettre au carré s'appelle n. Je mets 1 dans la mémoire n, pour commencer.	2) Mettre 1 dans la variable n;
J'appelle n deux fois et je multiplie ces valeurs; cela fait bien le carré de n.	3) Calculer n x n;
Le résultat est placé dans une nouvelle mémoire que je baptise C. Les baptêmes sont de ma responsabilité; je peux mettre ce que je veux.	4) Mettre cette valeur dans C;
J'imprime plusieurs choses à la file indienne. D'abord la valeur qui est dans n, puis une suite de caractères à imprimer tels quels, et enfin la valeur du carré qui est C. Ce qui donnera ici, par exemple: 1² = 1.	5) Imprimer "la valeur de n" suivi de " ² =" puis la "valeur de C";
C'est fini pour n = 1; je vais m'attaquer à n = 2 en ajoutant 1 dans la mémoire n (on dit aussi: j'incrémente n).	6) Ajouter 1 à n;
Je vérifie que la nouvelle valeur de n n'est pas égale au maximum que je me suis donné: ici, n = 2, et non pas 10. Alors, je recommence à partir de l'étape 3), car en 3) je calcule le carré de 2. C'est ce que je cherche à faire. Inutile de le récrire.	7) Si n = Max alors Arrêt, sinon recommencer à partir de 3;
En retrouvant l'instruction 6), j'ajoute 1 à n qui devient 3, nombre qui ne vaut pas 10; alors je vais à nouveau me retrouver en 3) qui donnera n = 4. Ainsi de suite.	Lorsque n = 10, valeur de Max, le déroulement de l'algorithme est terminé.

Pour simplifier …
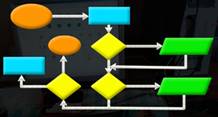
Pour simplifier et avoir une meilleure vision globale, on réalise une sorte de figure, un graphe, un organigramme. Voici l'algorithme de calcul des carrés sous la forme d'un organigramme. La partie initialisation permet de modifier les paramètres fixant le déroulement de l'algorithme. Max donne la quantité de carrés désirés, et n indique à partir de quelle valeur. Chaque rectangle est une instruction élémentaire. Ici, pour dire mettre 10 dans la mémoire nommée Max, on utilise le symbole ":=". On lit: M prend la valeur 10. C'est une affectation. La boucle est la partie répétitive de l'algorithme. Elle comporte toujours une condition d'arrêt, de fin. Un hexagone aplati indique un test dont le résultat est oui ou non (vrai ou faux). On indique clairement ce que l'on fait dans chacun des cas.	Imaginez une machine qui sait exécuter ces instructions, elle pourra le faire des milliers de fois sans se fatiguer et avec des valeurs aussi grandes que vous voulez.

Voir Exemple de recherche des nombres premiers (diaporama junior)

Affectation

L'affectation consiste à préciser la valeur d'une variable dans l'algorithme.

Si je veux affecter la valeur 10 à la variable baptisée Max, je note:

A := 10 (notation dans les programmes d'ordinateurs)

10 Max (notation sur les calculettes)

Bilan

Un algorithme est un mot savant pour dire "recette de calcul pour ordinateur". l'algorithme est universel: il fonctionne quelle que soit la machine utilisée. Cependant une transcription dans le langage propre de la machine utilisée sera indispensable. il est paramétrable: il est possible de choisir des valeurs avant de lancer l'exécution de l'algorithme. il est exigeant: toutes les choses à faire doivent être dites précisément et sans en oublier. Un algorithme comporte trois types d'instructions, plus un: ordre d'exécution (ajouter, multiplier, affecter …); test conditionnel (si ceci alors … sinon …); définition de boucle (faire 10 fois, tant que n <10 faire …); plus les instructions pilotant les entrées et les sorties de données. Tous les programmes du monde ont été et seront élaborés en utilisant des algorithmes. Cependant les informaticiens ont cherché à y échapper en inventant d'autres modes de traitement. Par exemple, en imitant le fonctionnement des neurones de l'homme ou même le comportement des animaux-sociaux.

S'exercer avec Scratch

Scratch: un jeu éducatif (gratuit sur Internet) qui permet la mise en place d'algorithmes et leur programmation sans que vous vous rendiez compte que vous programmez. Réalisation de scénettes. Plaisir immédiat. Usage en ligne ou téléchargement. Dès l'âge de 8 ans. Utilisé dans les écoles. Il n'existe pas plus simple !

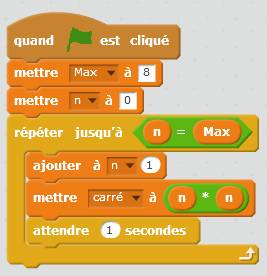
Calcul des carrés

Commentaire On construit le programme en fouillant dans les boites à outils. On sélectionne les instructions (les barres horizontales) pour les amener dans la zone de travail et les assembler comme indiqué sur la copie ci-contre. Le drapeau vert sert à démarrer le programme lorsqu'on clique dessus. On a créé les variables Max, n et carré avec les outils Données. La boucle répéter a été sélectionnée dans les outils Contrôle. L'égalité n = Max comme la multiplication n x n sont extraites des outils Opérateurs. On ajoute 1 à n avant au début de la boucle. On attend une seconde avant le nouveau passage dans la boucle, ceci pour laisser le temps de constater l'affichage de n et de son carré sur l'écran. En bas, l'affichage tel qu'il apparait en fin de programme: le carré de 8 est 64.

Exemple d'un algorithme simple

Étapes de construction d'une figure

Combien d'étapes pour que la figure comporte 439 carrés.

Principe du comptage

Pour passer d'une figure à la suivante on ajoute un élément à chacune des trois extrémités, soit + 3 à chaque itération:

S(n + 1) = S(n) + 3 avec S(1) = 1

On compte:

Itération	1	2	3	4	5	6	…	n	n + 1
Quantité	1	4	7	10	13	16	…	(S(n)	S(n) + 3

Formulation

La quantité croit en fois 3 en partant de quelque chose: S = 3n + k;

En prenant une valeur quelconque comme:

n = 4 et S = 10 => 10 = 3 x 4 + k => k = –2 et S = 3n – 2

Pour atteindre 439, quelle est la valeur de n?

439 = 3n – 2 => 3n = 441 => n = 147

Algorithme d'entraînement
On donne ce programme de calcul. Faire un tableau montrant le résultat pour tous les nombres suivants, choisis au départ: 10, 8, 6, 4, 2, 0, 1/2
En injectant 10, le résultat est 32. En injectant 6 ou 2, le résultat est nul. Il existe une plage entre 2 et 6 pour laquelle le résultat est négatif.
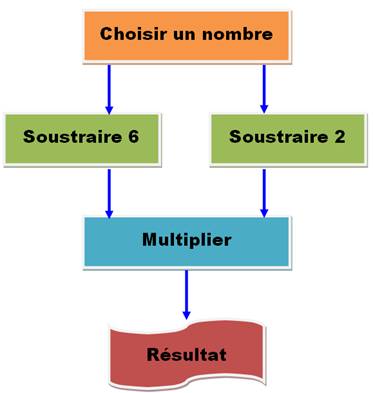
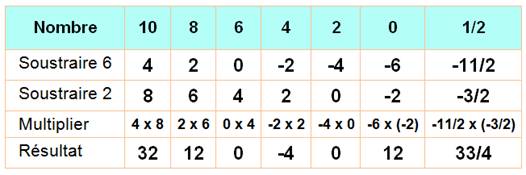
Traitement algébrique	L'opération exécutée par cet algorithme peut être mise en équation avec x comme variable d'entrée et y le résultat. y = (x – 6) (x – 2) Nous vérifions que la fonction s'annule bien pour x = 6 et x = 2. En développant: y = x² – 2x – 6x + 12 = x² – 8x + 12 Nous obtenons une fonction non-linéaire; Elle est du deuxième degré.

Cette question comptait pour 5 points sur 40 au Brevet de 2014

Suite	Algorithmes – Introduction Affichage de l'heure – Exemple Algorithme – Glossaire Mes premiers pas en programmation (en codage) Programmation – Index
Voir	Automate Dualité Énigmes et paradoxes Grands Hommes Histoire de l'informatique Histoire des ordinateurs Intelligence Intelligence des animaux Logique – Index Machine de Turing Multimédia et informatique – Index Outils de la logique Puissance de calcul Puzzles et énigmes – Index Raisonnement Réseaux neuronaux Systèmes experts Turing et le Bureau 47
Site	Algorithme pour l'apprenti programmeur
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Logique/IAalgorD.htm