|
Nombres a et b de même taille
dont
on retrouve leurs chiffres dans l'ordre
dans
a² + b²
1233, 8833, 990100, 94122353, 1765038125, 2584043776, 7416043776, 8235038125,
9901009901, 116788321168, 123288328768, 876712328768, 883212321168,
999900010000, 13793103448276, 15348303604525, 84651703604525, 86206903448276,
91103202846976, 92318202663025, …
Exemple: 9412² + 2353² = 94122353
Nombres a et b
de taille quelconque
dont
on retrouve leurs chiffres dans a² + b²,
pour
a et b jusqu'à 1000
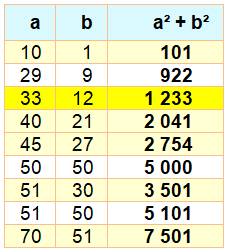
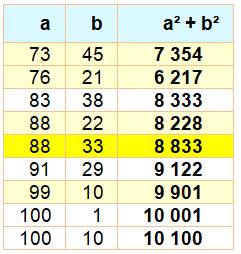
 Dans le même ordre: 88² + 33² = 8833
Dans le même ordre: 88² + 33² = 8833
 Dans l'ordre inverse: 33² + 12² = 1233
Dans l'ordre inverse: 33² + 12² = 1233
 Ou, plus généralement par permutation: 45² + 27² = 2754
Ou, plus généralement par permutation: 45² + 27² = 2754
|
|
|
a
|
b
|
a²
+ b²
|
|
10
|
1
|
101
|
|
33
|
12
|
1233
|
|
40
|
21
|
2041
|
|
45
|
27
|
2754
|
|
51
|
30
|
3501
|
|
70
|
51
|
7501
|
|
73
|
45
|
7354
|
|
76
|
21
|
6217
|
|
88
|
22
|
8228
|
|
88
|
33
|
8833
|
|
99
|
10
|
9901
|
|
100
|
10
|
10100
|
|
102
|
40
|
12004
|
|
102
|
94
|
19240
|
|
102
|
96
|
19620
|
|
108
|
54
|
14580
|
|
112
|
93
|
21193
|
|
117
|
45
|
15714
|
|
120
|
76
|
20176
|
|
145
|
27
|
21754
|
|
153
|
90
|
31509
|
|
162
|
37
|
27613
|
|
190
|
64
|
40196
|
|
201
|
40
|
42001
|
|
276
|
210
|
120276
|
|
280
|
45
|
80425
|
|
282
|
51
|
82125
|
|
285
|
160
|
106825
|
|
288
|
73
|
88273
|
|
295
|
60
|
90625
|
|
295
|
130
|
103925
|
|
295
|
150
|
109525
|
|
298
|
18
|
89128
|
|
301
|
201
|
131002
|
|
303
|
39
|
93330
|
|
307
|
118
|
108173
|
|
307
|
261
|
162370
|
|
324
|
171
|
134217
|
|
325
|
180
|
138025
|
|
330
|
120
|
123300
|
|
340
|
121
|
130241
|
|
340
|
132
|
133024
|
|
343
|
172
|
147233
|
|
351
|
190
|
159301
|
|
357
|
214
|
173245
|
|
358
|
168
|
156388
|
|
361
|
145
|
151346
|
|
|
a
|
b
|
a²
+ b²
|
|
381
|
265
|
215386
|
|
382
|
304
|
238340
|
|
387
|
154
|
173485
|
|
387
|
163
|
176338
|
|
387
|
198
|
188973
|
|
387
|
297
|
237978
|
|
397
|
190
|
193709
|
|
400
|
201
|
200401
|
|
400
|
210
|
204100
|
|
409
|
165
|
194506
|
|
412
|
393
|
324193
|
|
415
|
207
|
215074
|
|
417
|
328
|
281473
|
|
420
|
169
|
204961
|
|
420
|
232
|
230224
|
|
429
|
160
|
209641
|
|
430
|
256
|
250436
|
|
430
|
382
|
330824
|
|
438
|
228
|
243828
|
|
445
|
277
|
274754
|
|
450
|
270
|
275400
|
|
459
|
298
|
299485
|
|
462
|
168
|
241668
|
|
462
|
195
|
251469
|
|
471
|
220
|
270241
|
|
471
|
330
|
330741
|
|
475
|
220
|
274025
|
|
487
|
397
|
394778
|
|
490
|
228
|
292084
|
|
490
|
327
|
347029
|
|
490
|
453
|
445309
|
|
493
|
400
|
403049
|
|
493
|
438
|
434893
|
|
495
|
423
|
423954
|
|
498
|
438
|
439848
|
|
504
|
127
|
270145
|
|
504
|
387
|
403785
|
|
507
|
445
|
455074
|
|
508
|
304
|
350480
|
|
510
|
300
|
350100
|
|
510
|
493
|
503149
|
|
514
|
423
|
443125
|
|
516
|
213
|
311625
|
|
525
|
420
|
452025
|
|
546
|
273
|
372645
|
|
546
|
408
|
464580
|
|
564
|
237
|
374265
|
|
564
|
408
|
484560
|
|
567
|
234
|
376245
|
|
|
a
|
b
|
a²
+ b²
|
|
571
|
354
|
451357
|
|
573
|
214
|
374125
|
|
574
|
321
|
432517
|
|
574
|
508
|
587540
|
|
576
|
324
|
436752
|
|
577
|
495
|
577954
|
|
595
|
423
|
532954
|
|
600
|
493
|
603049
|
|
604
|
190
|
400916
|
|
627
|
538
|
682573
|
|
628
|
148
|
416288
|
|
628
|
537
|
682753
|
|
633
|
472
|
623473
|
|
634
|
102
|
412360
|
|
640
|
225
|
460225
|
|
645
|
210
|
460125
|
|
652
|
358
|
553268
|
|
655
|
420
|
605425
|
|
657
|
486
|
667845
|
|
661
|
421
|
614162
|
|
666
|
450
|
646056
|
|
667
|
576
|
776665
|
|
670
|
471
|
670741
|
|
670
|
534
|
734056
|
|
678
|
501
|
710685
|
|
696
|
150
|
506916
|
|
697
|
390
|
637909
|
|
697
|
520
|
756209
|
|
700
|
510
|
750100
|
|
702
|
549
|
794205
|
|
703
|
558
|
805573
|
|
703
|
586
|
837605
|
|
705
|
265
|
567250
|
|
705
|
285
|
578250
|
|
706
|
453
|
703645
|
|
708
|
426
|
682740
|
|
709
|
265
|
572906
|
|
709
|
634
|
904637
|
|
715
|
484
|
745481
|
|
718
|
483
|
748813
|
|
729
|
316
|
631297
|
|
729
|
639
|
939762
|
|
730
|
450
|
735400
|
|
738
|
577
|
877573
|
|
739
|
621
|
931762
|
|
741
|
508
|
807145
|
|
|
a
|
b
|
a²
+ b²
|
|
751
|
246
|
624517
|
|
760
|
210
|
621700
|
|
760
|
619
|
960761
|
|
765
|
109
|
597106
|
|
769
|
156
|
615697
|
|
769
|
385
|
739586
|
|
783
|
307
|
707338
|
|
783
|
415
|
785314
|
|
786
|
508
|
875860
|
|
787
|
313
|
717338
|
|
787
|
597
|
975778
|
|
789
|
376
|
763897
|
|
789
|
403
|
784930
|
|
789
|
507
|
879570
|
|
789
|
592
|
972985
|
|
796
|
214
|
679412
|
|
799
|
564
|
956497
|
|
801
|
297
|
729810
|
|
807
|
169
|
679810
|
|
807
|
439
|
843970
|
|
808
|
168
|
681088
|
|
810
|
397
|
813709
|
|
814
|
457
|
871445
|
|
835
|
247
|
758234
|
|
837
|
162
|
726813
|
|
838
|
172
|
731828
|
|
850
|
295
|
809525
|
|
873
|
145
|
783154
|
|
876
|
319
|
869137
|
|
877
|
138
|
788173
|
|
880
|
220
|
822800
|
|
880
|
330
|
883300
|
|
883
|
198
|
818893
|
|
885
|
240
|
840825
|
|
891
|
370
|
930781
|
|
897
|
363
|
936378
|
|
898
|
420
|
982804
|
|
901
|
280
|
890201
|
|
904
|
318
|
918340
|
|
904
|
358
|
945380
|
|
906
|
268
|
892660
|
|
907
|
283
|
902738
|
|
909
|
343
|
943930
|
|
910
|
351
|
951301
|
|
934
|
274
|
947432
|
|
940
|
201
|
924001
|
|
948
|
112
|
911248
|
|
960
|
201
|
962001
|
|
976
|
129
|
969217
|
|
990
|
100
|
990100
|
|
1000
|
100
|
1010000
|
|
![]()
![]()