NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/07/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Général	Diviseurs			Glossaire Général
INDEX Types de nombres	Somme carrée	Somme cube	Canadiens parfaits
	Sigma . Phi = k^4
	Sommaire de cette page >>> Définition >>> Liste >>> Statistiques >>> Somme des carrés des diviseurs

Famille	Nombre / Division
Définition	Nombre dont la somme des diviseurs est un carré.
Exemples	Les diviseurs de 3 sont 1 et 3; leur somme est 4 qui est un carré. La somme des diviseurs de 22 est 36 = 6². La somme des diviseurs de 66, 70, 94, 115 ou 119 est égale à 144 = 12².

Programmation Python	from sympy import divisors from sympy.ntheory.primetest import is_square for n in range(1, 100): s = sum(divisors(n)) if is_square(s): print(f"{n} → Sigma = {s},{divisors(n)} ")
		1 → Sigma = 1,[1] 3 → Sigma = 4,[1, 3] 22 → Sigma = 36,[1, 2, 11, 22] 66 → Sigma = 144,[1, 2, 3, 6, 11, 22, 33, 66] 70 → Sigma = 144,[1, 2, 5, 7, 10, 14, 35, 70] 81 → Sigma = 121,[1, 3, 9, 27, 81] 94 → Sigma = 144,[1, 2, 47, 94]
Version Python sans appel à sympy	import math def est_carre(n): racine = math.isqrt(n) return racine * racine == n def somme_diviseurs(n): return sum(i for i in range(1, n + 1) if n % i == 0) for nombre in range(1, 100): s = somme_diviseurs(nombre) if est_carre(s): print(f"{nombre} → sigma = {s}")

Voir Programmation – Index / Programmes Python – Index

Voir	Carrés Diviseurs Diviseurs somme carrée Diviseurs somme puissance Tables des sommes de diviseurs = puissance

Liste pour n jusqu'à 10 000 selon k croissant

Statistiques
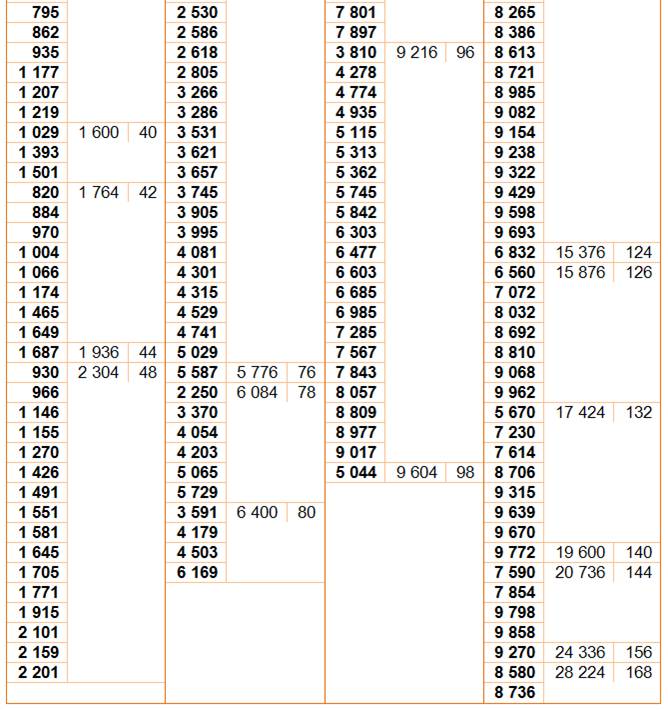
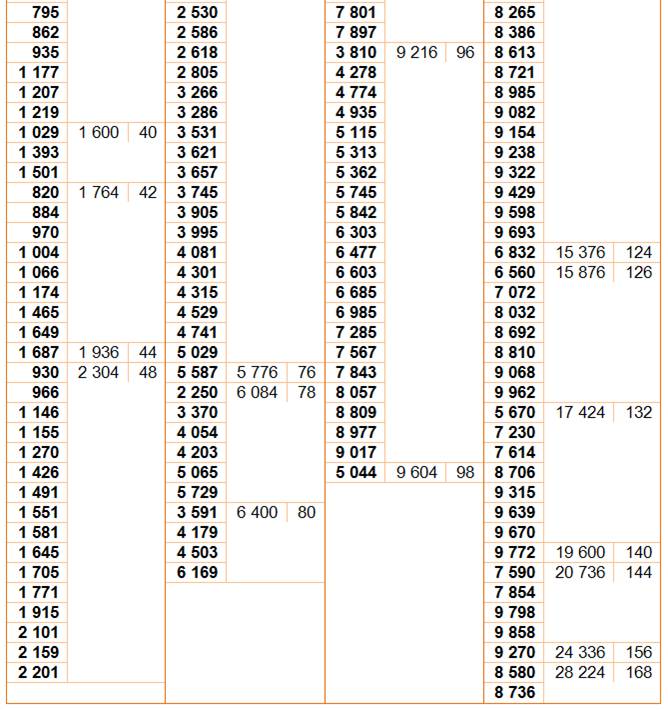
Jusqu'à n = 10 000, il y a: 270 nombres avec somme des diviseurs carrée, dont 120 avec la quantité de diviseurs également carrée, dont 74 avec quantité égale à 4 = 2², et 40 avec quantité égale à 16 = 4². Exemples 22 Somme = 36 = 6^2 et quantité = 4 = 2^2. 94 Somme = 144 = 12^2 et quantité = 4 = 2^2. 210 Somme = 576 = 24^2 et quantité = 16 = 4^2.

Somme des carrés des diviseurs
Nombres dont la somme des carrés des diviseurs est un carré. Exemple 42 => { 1, 2, 3, 6, 7, 14, 21, 42 } 1² + 2² + 3² + 6² + 7² + 14² + 21² + 42² = 2500 = 50²	[42, 50], [246, 290], [287, 290], [728, 850], [1434, 1690], [1673, 1690], [1880, 2210], [4264, 4930], [6237, 6710], [9799, 9802], [9855, 10660], [18330, 22100], [21352, 24650], [21385, 22100], [24856, 28730], [36531, 38918], [39990, 48100], [46655, 48100], [57270, 68900], [66815, 68900], [92664, 114070]
Nombres dont la somme des carrés des diviseurs est un cube.	[4182, 290], [4879, 290] Seuls jusqu'à n = 100 000

Voir Somme des cubes des diviseurs

Suite	Nombre dont la somme des diviseurs est un cube
Site	OEIS A006532 - Numbers whose sum of divisors is a square
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDIVIS/DivCarre.htm