Babbage Biographie

Machine à calculer pilotée par des cartes, comme celles du métier à tisser de Jacquard, qui alimentait la machine en instructions (premières cartes), puis en données (cartes suivantes).
Avant lui: Pascal et sa Pascaline et Leibniz et sa multiplicatrice.

Statistiques: tables d'espérance de vie.

Cryptologie (déchiffrage).

Optique (les phares).

Signalisation des chemins-de-fer (boîte noire).

Etc.

Publie six gros ouvrages et pratiquement 90 articles.

1791	0	Naissance à Walworth, Surrey.
1810	19	Trinity College puis Peterhouse.
1812	21	Fonde la Société Analytique avec d'autres mathématiciens.
1813	22	Première publication.
1814	23	Diplômé de Cambridge. Mariage: Georgina Whitmore
1816	24	Membre à la Société Royale de Londres.
1817	26	MBA
1820	29	Membre à la Société Royale d'Édimbourg.
1820	29	Fonde la Société Royale d'Astronomie.
1821	30	Plans de la première machine à différences.
1827	36	Décès de son épouse, de son père et de deux de ses enfants. Sur huit enfants, trois deviendront adultes.
1828	37	Chaire de mathématiques au Lucasian de Cambridge jusqu'en 1839.
1834	43	Principe de base d'une machine à calculer analytique (analytic engine) avec lecteur de cartes. Machine analytique de Babbage: un défi pour cette époque: machine mécanique; base 10 (pignons dentés à 10 positions); 40 décimales; une mémoire (magasin) de 1000 nombres de 50 chiffres. La machine analytique comprend déjà une partie arithmétique et logique, contrôle par boucles, branchements conditionnels. Et tout cet ensemble mécanique actionné par un moteur à vapeur. Voir Principe de fonctionnement de l'ordinateur
1842	51	Principe de programmation établis avec Ada Lovelace (1815-1852), fille de Lord Byron.
1847	56	Lance sa seconde machine à différences en simplifiant la première.
1871	80	Décès.
1908	/	Démonstration réussie du fonctionnement de la machine analytique par son fils.
1991	/	Construction de la seconde machine de Babbage: 8000 pièces, 5 tonnes. Fonctionnement comme prévu.

Ada Lovelace (1815-1862) – Augusta Ada King, comtesse de Lovelace

A 17 ans, elle rencontre Charles Babbage et se passionne pour son travail sur la machine à différences, puis sur la machine analytique. Visionnaire, Ada a su comprendre le potentiel de cette dernière machine peut-être encore plus que Babbage lui-même. Elle explique dans ses manuscrits, comment cette machine pourrait être programmée pour des tâches bien différentes que le calcul numérique.

Voir Ada Lovelace – Biographie

MACHINE DE BABBAGE

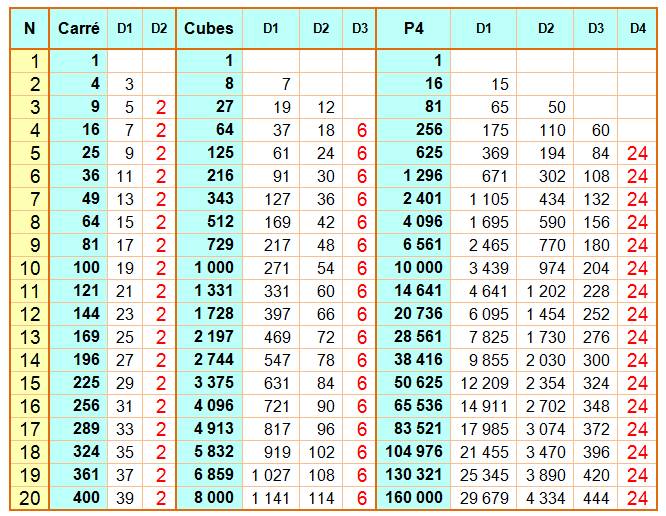
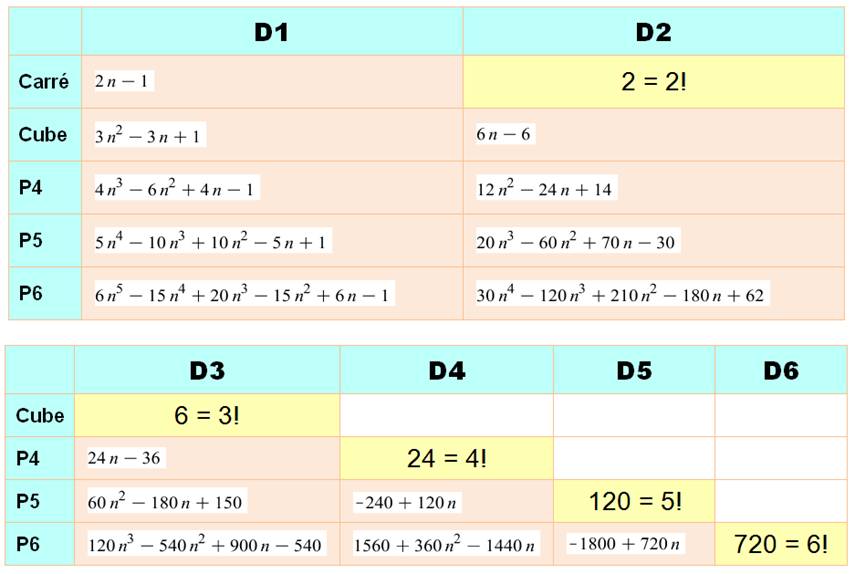
Le théorème utilisé par la machine à différences:

La différence d'ordre n des nombres successifs élevés à la puissance n est constante. Cette constante est égale à n! (factorielle n)

Voir Calculs sur les suites par la méthode des différences

Remarquez que D1 pour les carrés est égal à la somme de N et N-1. Que D2 pour les cubes est égal à 6 (N-1).

Voir Comment exprimer une factorielle par une somme?

Quelle merveille! Quel bijou de mécanique de précision!

The Babbage engine – Computer history museum (Voir la vidéo)

Voir Brève 48-948

Valeurs des différences d'ordre k selon la puissance

Table donnant l'expression de la différence kième entre deux puissances.

Exemple de lecture: en première différence (D1) entre carrés de nombres successifs, on trouve 2n – 1 qui indique que n² – (n – 1)² = 2n – 1.

Par exemple, pour n = 5: 5² – 4² = 9; en effet; 25 – 16 = 9.

La deuxième différence entre deux cubes de nombres successifs, on donne 6n – 6 qui est égal à = n³ – (n – 1)³ et qui se calcule de la manière suivante:

D1₁ = n³ – (n – 1)³ ; D1₂ = (n – 1)³ – (n – 2)³ et D2 = D1₁ – D1₂.

Par exemple pour n = 5: D1₁ = 5³ – 4³ = 61; D1₂ = 4³ – 3³ = 37 et D2 = 61 – 37 = 24 et la formule directe donne: 6 x 5 – 6 = 24.

Les formules sont calculées à partir de n et en descendant: n – 1, n – 2, etc.

On aurait pu symétriser en prenant n, n+1 et n-1 puis n+2 et n-2 … Amusant problème de développement des polynômes à l'aide des identités remarquables.

Exemple: la différence entre les carrés de deux nombres successifs est égale à 2n – 1 et entre deux cubes successifs: 3n² – 3 n + 1.

Application: connaissant un carré, pour passer au suivant, c'est très simple! Il suffit d'ajouter le nombre et son successeur. En effet, D1 = 2n – 1 = n + (n – 1). Par exemple, il est connu que 144 est le carré de 12. Pour trouver le carré de 13, j'ajoute 12 et 13 à 144, soit 169 qui est bien le carré de 13.

Voir Diapositive 8 de la découverte junior des carrés

Voir Développements sur les carrés - Index

Approche par les équations
Exemple avec n³ – (n – 1)³ Le résultat est une expression du deuxième degré (en effet, dans la différence, les termes au cube s'éliminent).	n³ – (n – 1)³ = an² + bn + c Trois inconnues: a, b et c
Prenons trois valeurs faciles à calculer.	n = 1: 1³ – 0 = 1 = a + b + c n = 2: 2³ – 1³ = 7 = 4a + 2b + c n = 3: 3³ – 2³ = 17 = 9a + 3b + c
Résolution (tous calculs faits) Voir Résolution semblable	n³ – (n – 1)³ = 3n² – 3n + 1

Voir Différences secondes constantes

Approche par développement
Développement de n^k – (n – 1)^k	Identité remarquable générale a^k – b^k = (a – b) x (a^k–1 + a^k–2 b + ... + ab^k–2 + b^k–1) Voir Identités remarquables Pour deux nombres consécutifs n et (n – 1) n^k – (n – 1)^k = (n^k–1 + n^k–2 (n–1) + ... + n(n–1)^k–2 + (n–1)^k–1) Exemple pour k = 3 n³ – (n – 1)³ = n^3–1 + n^3–2 (n – 1) + (n – 1)^3–1 = n² + n² – n + n² – 2n + 1 = 3n² – 3n + 1
Généralisation et propriété remarquable	La différence kième entre la puissance kième de nombres successifs est constante et égale à k!. Voir calcul de la différence kième entre la puissance de nombres consécutifs >>>

Vidéo

Calcul de la puissance kièmes d'un nombre par Yves Roques – Vidéo – Explication très claire sur tableau blanc.

Courtoisie de l'auteur lui-même que je remercie

Voir	Calcul des Carrés Calcul des Cubes Factorielle Initiation aux dérivées via les carrés et les cubes Histoire des ordinateurs Somme des entiers, carrés … avec calcul des différences
Diconombre	Nombre 2 Nombre 6 Nombre 24
Aussi	Conjecture de Catalan Contemporains (Années1700) Contemporains (Années1800) Coût du bit (historique) Identités Jeux – Index Multimédia et informatique – Index Puissance – Index
Sites	Babbage – Wikipédia The Babbage engine – Computer history museum – Vidéo qui montre le fonctionnement Charles Babbage – Biography Les différences kièmes des puisnaces e nombres consécutifs – Vidéo – Yves Roques
Cette page	http://villemin.gerard.free.fr/aBiograp/Babbage.htm