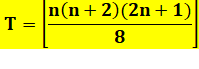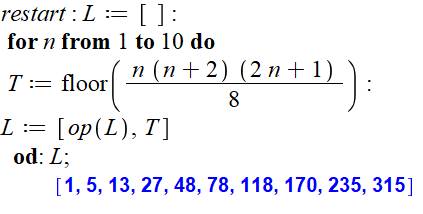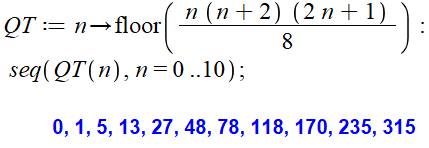Quantité de triangles équilatéraux dans le triangle équilatéral

Édition du: 18/01/2025

INDEX Défis en géométrie Types de triangles Triangle Dénombrement	Triangles – Particularités
	Triangulation	Carrés & triangles	Qté de triangles dans une figure
	Point et triangles	Triangles trois en cinq	Qté dans le triangle équilatéral
	Quatre triangles	Carrés & triangle rectangle	Qté de triangles –Méthode
	Cercles et triangles

Faites un double-clic pour un retour en haut de page

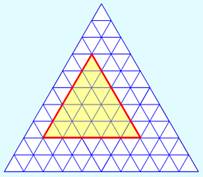
Quantité de Triangles équilatéraux

dans le triangle équilatéral

On se donne une grille de triangles équilatéraux puis on y dessine un triangle équilatéral de dimension n (ici en rouge).

Le but consiste à compter les triangles équilatéraux reposant sur la grille et contenus dans ce triangle. Oui, on doit compter les petits triangles, les moyens et les plus gros. Formule ?

Raffinement: est-il possible d'imaginer des triangles équilatéraux ayant pour sommets les points de la grille sans épouser le lignage de la grille ? Réponse: oui !

Sommaire de cette page

>>> Dénombrement des triangles équilatéraux

>>> Triangles équilatéraux élémentaires

>>> Tous les triangles équilatéraux de la grille

>>> Calcul du total des triangles

>>> Triangles équilatéraux OBLIQUES

Débutants

Nombres

Glossaire

Nombres

Dénombrement des triangles équilatéraux		haut
But Il s'agit de compter les triangles équilatéraux contenus dans un grand triangle équilatéral de dimension n de côté. Les sommets des triangles sont tous situés sur les point d'une grille Trois cas de comptage Il existe au moins trois cas de dénombrements: compter les triangles élémentaires de dimension 1 avec tête en haut ou tête en bas. Il y en a 16 = 4²; >>> compter les triangles de toutes tailles alignés sur la grille: 1, 2, 3 et 4. Il y en a 27 dont les 16 petits; >>> compter en plus les triangles équilatéraux en oblique: ayant pour sommets ceux de la grille sans reposer sur le lignage de la grille Il y en a 8: 6 moyens et 2 grands. >>>	Grille de triangles équilatéraux dans un triangle équilatéral de dimension 4 Exemple triangle oblique
Exemple avec n = 5 Dans ce triangle équilatéral de dimension 5, il existe 70 triangles. 25 triangles élémentaires de dimension 1; 23 triangles de dimension 2, 3, 4 et 5; et 22 triangles de dimension en racine de 3. Cas des triangles équilatéraux obliques (en √3) Leurs sommets sont sur les points de la grille mais leur côté n'épousent pas le lignage de cette grille.	Triangle de dimension 5 contenant 70 triangles équilatéraux de toutes tailles

Voir Brève 59-1176

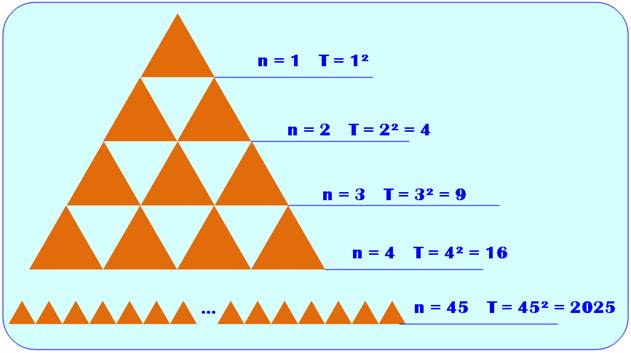
Triangles équilatéraux élémentaires

haut

Quantité de triangles équilatéraux ÉLÉMENTAIRES dans un triangle équilatéral

T_e(n) = n² (n est le côté du triangle)

Pour n = 4, T_e(4) = 4² = 16, dont 10 avec tête en haut et 6 avec tête en bas

La quantité de triangles, tête en haut et tête en bas, sur une ligne est égale au nombre impair suivant la quantité de la ligne du dessus. Il y en a successivement: 1, 3, 5, 7… par ligne.
Or, la somme des nombres impairs est un carré.

La dernière ligne illustre le cas du nombre 2025, le carré de 45, alors, il y a 2025 triangles équilatéraux élémentaires dans le triangle équilatéral de dimension 45. Voir Brève 60, Année 2025

Tous les triangles équilatéraux de la grille		haut
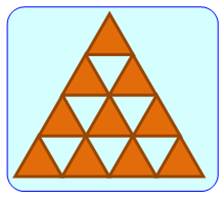
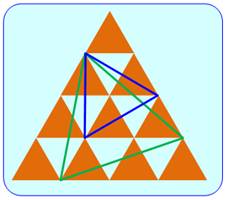
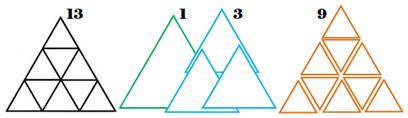
But Compter les triangles équilatéraux de toutes tailles dans un triangle équilatéral de taille n. Ces triangles reposent sur le lignage de la grille. Chacun est composé de k triangles élémentaires.	Exemple pour n = 3 Cette figure de gauche comporte 13 triangles équilatéraux. Dont 1 grand (vert) et 9 petits (bruns) faciles à dénombrer. Plus 3 moyens (bleus) à ne pas oublier.
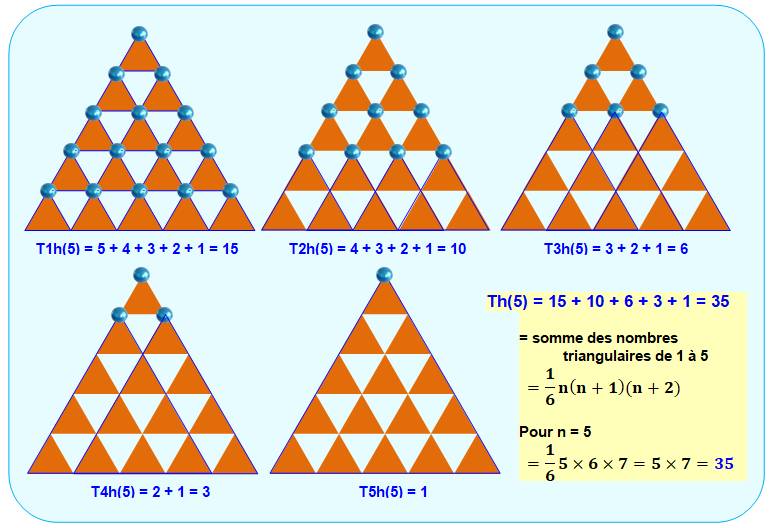
Principe du dénombrement: compter les têtes Il s'agit de compter les triangles de taille 1, 2, 3, … n avec une tête en haut ou une tête en bas. Exemple avec n = 5 – Tête en HAUT La méthode consiste à repérer les têtes en haut (billes bleues) pour les différentes tailles de triangles. Nous sommes ramenés au cas simple du dénombrement des triangles élémentaires tête en haut. pour la taille 1 (T1), tête vers le haut (T1h) avec n = 5, on a: T1h(5) = 15, la somme des entiers de 1 à 5, soit le nombre triangulaire T₅ qui vaut 5 × 6 / 2 = 15. pour la taille 2, T2h(5) = 10, la même chose que T1 sans la ligne du bas: c'est le nombre triangulaire 3, T₄ = 1 + 2 + 3 + 4 = 4 × 5 / 2 = 10. Etc. Au total, il s'agit de la somme des nombres triangulaires de 1 à 5: Th(5) = 1 + 3 + 6 + 10 + 15 = 35. Cette somme est connue comme nombre tétraédrique. Elle vaut: 1/6 n (n + 1) (n + 2). Pour n= 6, on aurait: 6 × 7 × 8 / 6 = 56 triangles tête en haut

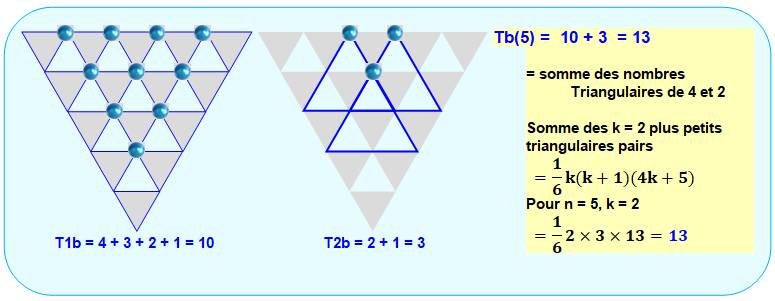
Exemple avec n = 5 – Tête en BAS

Il s'agit de compter les triangles blancs. On a retourné la figure de manière à se ramener aux cas déjà vus. En effet, comme précédemment, on compte les têtes des triangles blancs (billes bleues).

pour la taille 1 (T1), tête vers le bas (T1b), il y a 1 + 2 + 3 + 4 = 10 triangles.

pour la taille 2 (T2), tête vers le bas (T2b), il y a 1 + 2 = 3 triangles.

Au total, il s'agit de la somme des nombres triangulaires de 2 et 4: Tb(5) = 3 + 10 = 13.
Cette somme est connue comme la somme des nombres triangulaires pairs.
Elle vaut: 1/6 k (k + 1) (4k + 5) avec k = (n – 1) / 2.

Finalement, le triangle de côté 5 comprend: 35 triangles tête en haut et 13 tête en bas, soit un total de 48.

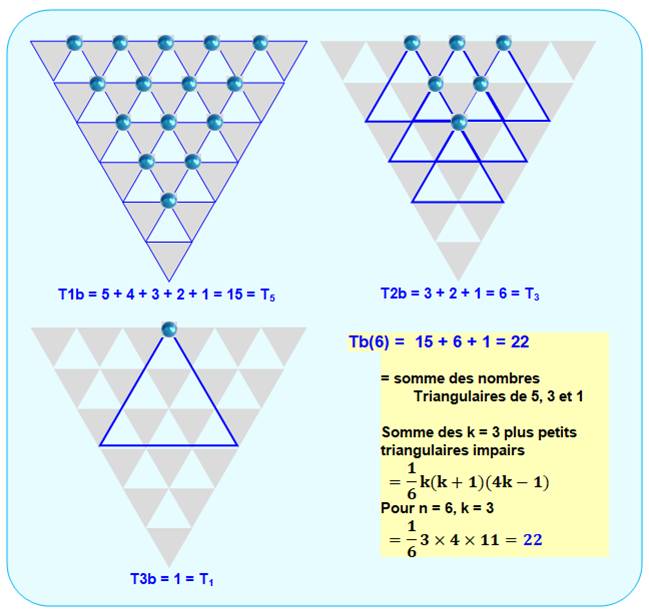
Exemple avec n = 6 – Tête en BAS

Cet exemple illustre le fait que le compte des triangles à tête vers le bas diffère selon que n est pair ou impair.

Pour l'un, il s'agit de la somme des nombres triangulaires PAIRS et pour l'autre des nombres triangulaires IMPAIRS.

Cette somme est connue. Elle vaut: 1/6 k (k + 1) (4k – 1) avec k = n / 2.

Finalement, le triangle de côté 6 comprend: 56 triangles tête en haut et 22 tête en bas, soit un total de 78.

Calcul du total des triangles

haut

Calcul du total

Il s'agit de calculer la quantité de triangles de toutes tailles contenus dans un triangle équilatéral de dimension n.

On reprend les expressions calculées plus haut en les développant.

La somme est calculée selon que n, le côté du grand triangle, est impair ou pair.

Note: les calculs intermédiaires ne sont pas développés.

Calcul selon que n est impair ou pair

Formule unique

avec l'opérateur PLANCHER

Programmes Maple

Note: Plancher se dit floor en anglais.

Simple

Avancé

Quantité de triangles

selon la valeur de n à partir de 1 et jusqu'à 100.

1, 5, 13, 27, 48, 78, 118, 170, 235, 315, 411, 525, 658, 812, 988, 1188, 1413, 1665, 1945, 2255, 2596, 2970, 3378, 3822, 4303, 4823, 5383, 5985, 6630, 7320, 8056, 8840, 9673, 10557, 11493, 12483, 13528, 14630, 15790, 17010, 18291, 19635, 21043, 22517, 24058, 25668, 27348, 29100, 30925, 32825, 34801, 36855, 38988, 41202, 43498, 45878, 48343, 50895, 53535, 56265, 59086, 62000, 65008, 68112, 71313, 74613, 78013, 81515, 85120, 88830, 92646, 96570, 100603, 104747, 109003, 113373, 117858, 122460, 127180, 132020, 136981, 142065, 147273, 152607, 158068, 163658, 169378, 175230, 181215, 187335, 193591, 199985, 206518, 213192, 220008, 226968, 234073, 241325, 248725, 256275.

OEIS A002717 – Number of triangles in triangular matchstick

arrangement of side n

Triangles équilatéraux OBLIQUES

haut

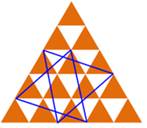
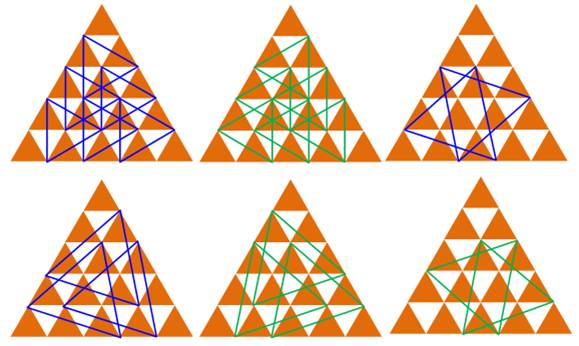
Cas n = 4

La figure montre les huit triangles équilatéraux obliques existant sur la grille de dimension 4.

Les sommets de ces triangles sont les points de la grille, mais les côtés n'épousent pas le lignage de la grille. Autrement-dit, la longueur des côtés de ces triangles équilatéraux ne sont pas des nombres entiers, mais des nombres en racine de 3, des nombres irrationnels.

3 + 3 + 2 = 8

Cas n = 5

On dénombre vingt-deux triangles obliques de trois tailles.

6 + 6 + 3 + 3 + 2 + 2 = 22

Cas n = 6

Il y a 48 triangles obliques.

Si on numérote les sommets de la grille de 1 à 7 sur la ligne du bas puis en poursuivant de bas en haut et de gauche à droite, les triplets de sommets des triangles obliques sont:
{2, 10, 14}, {2, 11, 19}, {2, 12, 23}, {2, 13, 26}, {3, 8, 15}, {3, 11, 15}, {3, 12, 20}, {3, 13, 24}, {3, 17, 19}, {3, 18, 23}, {4, 8, 20}, {4, 9, 16}, {4, 12, 16}, {4, 13, 21}, {4, 14, 21}, {4, 18, 20}, {5, 8, 24}, {5, 9, 21}, {5, 10, 17}, {5, 13, 17}, {5, 14, 25}, {5, 15, 22}, {6, 8, 27}, {6, 9, 25}, {6, 10, 22}, {6, 11, 18}, {9, 16, 19}, {9, 17, 23}, {9, 18, 26}, {10, 14, 20}, {10, 17, 20}, {10, 18, 24}, {10, 22, 23}, {11, 14, 24}, {11, 15, 21}, {11, 18, 21}, {11, 19, 25}, {12, 14, 27}, {12, 15, 25}, {12, 16, 22}, {15, 21, 23}, {15, 22, 26}, {16, 19, 24}, {16, 22, 24}, {17, 19, 27}, {17, 20, 25}, {20, 25, 26}, {21, 23, 27}.

Cas n = 7

Il y a 92 triangles obliques.
{2, 11, 16}, {2, 12, 22}, {2, 13, 27}, {2, 14, 31}, {2, 15, 34}, {3, 9, 17}, {3, 12, 17}, {3, 13, 23}, {3, 14, 28}, {3, 15, 32}, {3, 19, 22}, {3, 20, 27}, {3, 21, 31}, {4, 9, 23}, {4, 10, 18}, {4, 13, 18}, {4, 14, 24}, {4, 15, 29}, {4, 16, 24}, {4, 20, 23}, {4, 21, 28}, {4, 26, 27}, {5, 9, 28}, {5, 10, 24}, {5, 11, 19}, {5, 14, 19}, {5, 15, 25}, {5, 16, 29}, {5, 17, 25}, {5, 21, 24}, {5, 22, 30}, {6, 9, 32}, {6, 10, 29}, {6, 11, 25}, {6, 12, 20}, {6, 15, 20}, {6, 16, 33}, {6, 17, 30}, {6, 18, 26}, {7, 9, 35}, {7, 10, 33}, {7, 11, 30}, {7, 12, 26}, {7, 13, 21}, {10, 18, 22}, {10, 19, 27}, {10, 20, 31}, {10, 21, 34}, {11, 16, 23}, {11, 19, 23}, {11, 20, 28}, {11, 21, 32}, {11, 25, 27}, {11, 26, 31}, {12, 16, 28}, {12, 17, 24}, {12, 20, 24}, {12, 21, 29}, {12, 22, 29}, {12, 26, 28}, {13, 16, 32}, {13, 17, 29}, {13, 18, 25}, {13, 21, 25}, {13, 22, 33}, {13, 23, 30}, {14, 16, 35}, {14, 17, 33}, {14, 18, 30}, {14, 19, 26}, {17, 24, 27}, {17, 25, 31}, {17, 26, 34}, {18, 22, 28}, {18, 25, 28}, {18, 26, 32}, {18, 30, 31}, {19, 22, 32}, {19, 23, 29}, {19, 26, 29}, {19, 27, 33}, {20, 22, 35}, {20, 23, 33}, {20, 24, 30}, {23, 29, 31}, {23, 30, 34}, {24, 27, 32}, {24, 30, 32}, {25, 27, 35}, {25, 28, 33}, {28, 33, 34}, {29, 31, 35}

Haut de page (ou double-clic)

Suite	*Voir* Haut de page Carré maximum dans le triangle rectangle Triangles et cercles Jeux et énigmes – Index Triangle – Index
Voir	Allumettes Angle Arbres de distribution Carré dans le triangle, construction astucieuse Carrés Cercle DicoMot Droite Éléments de géométrie Géométrie Nombres triangles Polygone Relations dans les triangles Somme de r puissances k Triangle de Calabi et ses trois carrés dans le triangle Triangles Triangles – Types Trigonométrie
Site	Combien y a-t-il de triangles – The Dude Number of equilateral triangles in triangular grid How Many Triangles Are There? Learn The Formula For Any Size! – MindYourDecision – Video Counting the number of Triangles \| How many equilateral triangles? – Making Mathematics Meaningful – Video
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/QteTrTr.htm