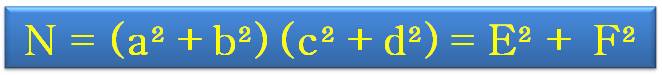|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Identités de BRAHMAGUPTA ou de DIOPHANTE, FIBONACCI, BACHET,
LAGRANGE À première vue, une identité magique
Le produit d'une somme de
deux carrés donne aussi une somme de
deux carrés et même souvent de deux façons différentes. Utilisée pour la résolution d'équations
diophantiennes (Pell-Fermat). |
Voir page similaire: Somme de deux carrés et imaginaires
|
|
||
|
Observation Voyez ces exemples. Dès qu'un nombre peut
s'exprimer sous forme d'un produit de somme de deux carrés (SDC), il est automatiquement somme de deux
carrés. |
50 = (1² + 2²) (1² + 3²) = 1² + 7² = 5² +
5² 65 = (1² + 2²) (2² + 3²) = 1² +
8² = 4² + 7² 68 = (1² + 1²) (3² + 5²) = 2² + 8² 533 = (2² + 3²) (4² + 5²)
= 2² + 23² = 7² + 22² SDC x SDC = SDC |
|
|
|
||
|
La somme des deux
carrés est aussi égale à la somme de quatre carrés. |
N = (a² + b²) (c² + d²) = a²c² + a²d² + b²c² + b²d² = (ac)² + (ad)² + bc)² + (bd)² (1) |
|
|
Pour aller plus loin,
il nous faut un truc tout bête lorsqu'il est dévoilé. Ajouter et soustraire
une même expression de manière à former des carrés. Facile, lorsqu'on se
souvient des identités remarquables
de base (a + b)² = a² + 2ab + b |
N = a²c² + b²d² + 2abcd + a²d² +
b²c² – 2abcd = (ac + bd)² +
(ad – bc)² (2) |
|
|
Nous aurions pu
inverser l'addition et la soustraction. D'où la formation d'une
deuxième somme de deux carrés. Elle est parfois identique à la première à une
commutation près des termes. |
N = a²c² + b²d² – 2abcd + a²d² +
b²c² + 2abcd = (ac – bd)² +
(ad + bc)² (3) |
|
|
Exemple
avec 50 Avec une coquetterie,
car 50 est le produit de sommes de deux carrés de deux façons
différentes |
50
= (1² + 2²) (1² + 3²) = 1² + 3²
+ 2² + 6² = 1 + 9 + 4 + 36 (1) = (1 + 6)²
+ (3 – 2)² = 7² + 1² (2) = (1 – 6)²
+ (3 + 2)² = 5² + 5² (3) 50
= (1² + 1²) (3² + 4²) = 3² + 4²
+ 3² + 4² = 9+ 16 + 9 + 16 (1) = (3 + 4)²
+ (4 – 3)² = 7² + 1² (2) = (3 – 4)²
+ (3 + 4)² = 1² + 7² (3) |
|
Voir
Table
|
|
||
|
Deux
carrés N = (a² + b²) (c² + d²) = E² + F² Deux
carrés généralisés N = (a² + Nb²) (c² + Nd²) = E² + NF² Trois et
quatre carrés N = (a² + b² + c²) (a'² + b'² + c'²) = (aa' +
bb' + cc')² + (ab' - a'b)² + (bc' - b'c)²
+ (ca' - c'a)² |
de Diophante ou de Bachet >>> de Brahmagupta ou de Fibonacci >>> de Lagrange >>> |
|
|
|
|
|
- Diophante d'Alexandrie (grec) découvre le
premier l'identité: (a² – b²)(c² – d²) = (ac + bd)² – (ad + bc)² - 628
– Brahmasphutasiddhanta, ouvrage de Brahmagupta
(598 – 668), mathématicien et astronome indien. Il y redécouvre l'identité
qui portera son nom. Mohammad al-Farazi traduit les textes de Brahmagupta du
sanskrit en arabe. - 1150
– Généralisation de Bhaskara II (a² – kb²)(c² – kd²) = (ac + kbd)² – k(ad +
bc)² - 1126
– Traduction en latin - 1225
– Fibonacci, dans Liber quadratorum, énonce
cette identité dans son ouvrage sur les carrés. - Euler généralise avec quatre carrés, identité qui
servira dans la formation des quaternions. Rappel:
Tout nombre entier est la somme de quatre carrés - Extension
à huit carrés avec les nombres de Cayley ou octonions |
|
Voir Diophante, Fibonacci, Euler, Contemporains
|
|
|
|
Brahmagupta's
identity says that the product of two numbers, each of
which being a sum of two squares, is itself a sum of two squares. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Biographies |
|
|
Cette
page |
http://villemin.gerard.free.fr/aMaths/Puissanc/Carres/Brahma1.htm |
![]()