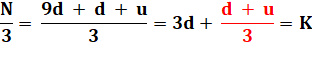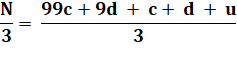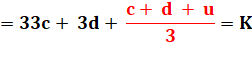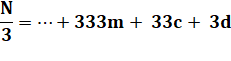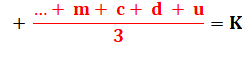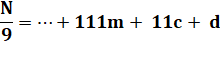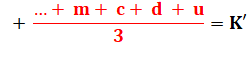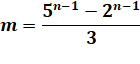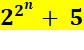|
|||||||||||||||||||||||||||||
![]()
En bref

|
DIVISIBILITÉ p Critères de divisibilité et
formes polynomiales divisibles. Rappel: la Racine numérique (RN) d'un nombre est
la somme de ses chiffres, répétée jusqu'à obtenir un nombre à un seul
chiffre. Ex: 1234 => 1 + 2 + 3 + 4
= 15 et 15 => 1 + 5 = 6 Souvenez-vous: un nombre (n)
divisé par trois donne un reste de 0, 1 ou 2; ou en symétrisant: –1, 0 ou +1.
On note n = {3k – 1; 3k;
3k +1}. Ce qui veut dire que tout nombre peut s'écrire: 3k – 1 ou 3k
ou 3k + 1. Rien d'autre! |
Devinette: deux nombres divisibles par 3
|
Prenez
deux nombres (a et b) au hasard, leur somme (s) et leur différence (d).
Alors, l'un de ces quatre nombres (a, b, s, d), au moins, est divisible par
3. 3 La barre verticale signifie divise. On lit: trois divise l'un des nombres
a, b, s ou d. Démonstration Si
l'un des deux nombres (a ou b) est divisible par 3, c'est bon. Si les deux ne
sont pas divisibles par 3, alors voyons la somme et la différence de tels
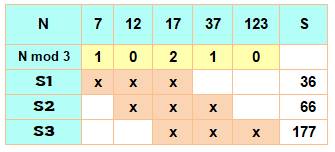
nombres dont le reste de la division par 3 est soit 1 soit -1:
Les
cas marqués en jaune, en quinconce, prouve la divisibilité par 3 dans tous
les cas. Exemples:
7 + 5 = 12 = 3 x 4; 8 – 5 = 3; 10 + 5 = 15 = 3 x 5; etc. |
|
|
||||
|
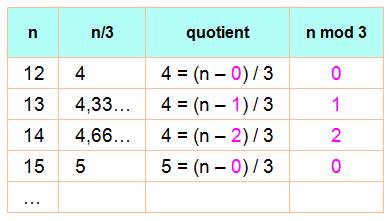
Plancher (n/3) = (n – n mod 3) / 3
Note: cette
propriété est valable pour toute division en adaptant l'argument du modulo. Démonstration selon la
valeur de n mod 3 |
|
|||
|
n mod 3 = 0 |
n mod 3 = 1 |
n mod 3 = 2 |
||
|
n = 3q |
n = 3q + 1 |
n = 3q + 2 |
||
|
n/3 = q |
(n – 1) / 3 = q |
(n – 2) / 3 = q |
||
Anglais pour plancher: floor
|
|
||
|
Un nombre est
divisible par 3 si la somme de ses chiffres est divisible par 3. Voir Démonstration / Divisibilité par 9 Si un nombre est
divisible par 3 toute permutation de ses chiffres est divisible par 3. En effet, quelle que la
position des chiffres, la somme reste identique. |
123 => RN = 6 => oui, divisible par 3 124 => RN = 7 => non divisible par 3 12345
=> 15 => 6 => oui 123456789
=> 45 => 9 => oui 111 => 3 => oui 777 => 21 => 3 => oui 100000010000001 => 3 => oui 123 = 3 x
41 132 = 3 x
44 213 = 3 x
71 231 = 3 x
77 312 = 3 x 104 321 = 3 x 107 |
|
Voir Somme / Permutation/ Semi-pannumériques
|
|
||
|
Divisibilité d'un nombre à deux
chiffes Un nombre
N peut s'écrire avec ses
dizaines (d) et ses unités (u), comme indiqué. |
N = 10d + u N = 9d + d + u Par
exemple: 25 = 2 x 10 + 5; ici d = 2 et u = 5. |
|
|
Pour que
N soit divisible par 3, il faut que N/3 soit un nombre
entier K. |
|
|
|
Seule possibilité
pour que K soit entier: |
d + u
divisible par 3 |
|
|
Divisibilité d'un nombre à trois
chiffes Un nombre
N peut s'écrire avec ses centaines (c),
dizaines (d) et ses unités (u), comme indiqué. |
N = 100c + 10d + u N = 99c + 9d + c + d + u |
|
|
Pour que
N soit divisible par 3, il faut que N/3 soit un nombre entier K. |
|
|
|
Seule
possibilité: |
c + d + u
divisible par 3 |
|
|
Divisibilité d'un nombre à n
chiffres Toutes les
puissances de 10 sont divisible par 3 à un près. Comme pour deux ou trois
chiffres, on retrouvera |
|
|
|
Qui
conduit à la généralisation |
N est divisible par 3 si la somme des chiffres
est divisible par 3. |
|
|
Divisibilité par 9 Observez
que l'on peut diviser par 9 |
|
|
|
Conclusion
immédiate: |
N est divisible par 9 si la somme des
chiffres est divisible par 9. |
|
|
Méthode par modulo pour trois
chiffres On
indique mod pour signifier que l'on ne
s'intéresse qu'aux restes de la division par 3. Par exemple 10 |
N = 99c + 9d + c + d + u
|
|
|
Un nombre
est divisible par 3 si son modulo 3 est nul. |
Qui se lit: 3 divise N si (c+d+u) est
congru à 0 modulo 3. |
|
|
Méthode générale avec les modulos |
|
|
|
Or: |
|
|
|
On peut
écrire: |
|
|
|
Multiple
de 9 (et a fortiori de 3) si: |
|
|
|
Cad. |
|
|
Voir Divisibilité
par 9
|
Ce
monsieur passe à la caisse avec:
Le monsieur signale
poliment à la personne de la caisse qu'il doit y avoir une erreur. Comment le
sait-il? |
|
|
||
|
3 3 3 La barre verticale se lit: "divise". Le produit de trois nombres successifs est divisible par
3. Le cube de n diminué de n est divisible par 3. En fait divisible
par 6 >>> Explication: parmi trois nombres successifs,
il en est toujours un qui est divisible par 3. De sorte que cette propriété
est vraie pour trois nombres successifs ou plus. Les permutations des
chiffres sont également divisibles par 3. Le carré de n diminué de 1 est divisible par 3 si
n ne l'est pas. |
1
x 2 x 3 = 3 x
2 2
x 3 x 4 = 3 x
6 3
x 4 x 5 = 3 x 20 4
x 5 x 6 = 3 x 40 5
x 6 x 7 = 3 x 70 33
– 3 = 27 – 3 = 24 = 3 x
8 43
– 4 = 64 – 4 = 60 = 3 x 20 53
– 5 = 125 – 5 = 120 = 3 x 40 11
x 12 x 13 x 14 = 3 x 8008 = 24 024 6
x 7 x 8 = 336 = 3 x 112 633 = 3 x 211 6
=> 6² – 1 = 35 7
=> 7² – 1 = 48 = 3 x 16 8
=> 8² – 1 = 63 = 3 x 21 9
=> 9² – 1 = 80 Explication: (3k + 0)²
= 9k² + 0 (3k + 1)²
= 9k² + 6k + 1 (3k – 1)²
= 9k² – 6k + 1 |
|
|
La concaténation des
chiffres de trois nombres successifs est divisible par 3. Soit un des nombres
divisible par 3; ses deux voisins se compensent: l'un est divisible par 3 à
-1 près et l'autre à +1 près. L'ensemble est divisible par 3.
Si le nombre
central est divisible par 3, les nombres formés sont également divisibles par
9. En effet, si n central
divisible par 9; ses deux voisins s'annihilent dans la division par 9. |
123 = 3 x 41 234 = 3 x 78 345 = 3 x 115 RN(n) = 3k RN(n-1) = 3k' – 1 RN(n+1)
= 3k" + 1 RN
(de tous) = 3 (k+k'+k") 232 425 = 3 x 77 475 222 345 = 3 x 74 115 543 222 = 3 x 181 074 997 998 999 = 3 x 332 666 333 995 996 997 = 9 x 110 666 333 RN(n) = 0 RN(n-1) = – 1 RN(n+1)
= + 1 RN
(de tous) = 0 |
|
Voir Carré
/ Cube / Concaténation / Divisibilité par 9 / Calcul mental
Combien de nombres divisibles par 3 ?
|
Avec
les chiffres {0, 1, 2, 3, 4, 5} combien peut-on former de nombres à cinq
chiffres divisibles par 3? |
|
|
||
|
Parmi
cinq nombres quelconques, pas nécessairement distincts, il en existe toujours
trois dont la somme est divisible par 3 (S3). Exemple (ici, trois sommes possibles)
Parmi
quatre nombres, la probabilité d'obtenir S3 divisible par 3 est: 70,3%. Et pour
trois nombres, elle est de 34,4%. |
Sachant que le reste de la division par 3 est 0, 1 ou 2, on déduit: Cas 1 Si trois restes parmi les cinq sont égaux, leur somme est divisible
par 3. Exemple avec le reste 2: 2 + 5 + 11 = 18, divisible par 3. Cas 2 Dans le cas contraire, les seuls combinaisons de restes possibles sont:
(0, 0, 1, 1, 2) ou (0, 0, 1, 2, 2) ou (0, 1, 1, 2, 2), sinon, il y en aurait
trois égaux. En choisissant les nombres dont les restes sont (0, 1, 2), la somme
sera divisible par 3. Exemple: 3 + 4 + 5 = 12, divisible par 3. |
|
|
Généralisation Démonstration
due à Erdös et Ziv – 1961 |
Théorème Parmi 2n – 1 nombre positifs, on peut toujours en
choisir n tel que leur somme est divisible par n. |
|
Voir Congruence
(mod)
Cycle en 153
|
Tous les nombres divisibles par 3 ont un cycle-cube qui se termine par 153. Le cycle-cube consiste à faire la somme des
cubes des chiffres du nombre et à recommencer sur la somme obtenue. Exemple:
93 = 729 => 73 + 23 + 93 =
1080 => 13 + 83 = 513 => 53 + 13
+ 33 = 153 |
|
|
||
|
3 si A et B non multiple de 3 La différence de deux carrés est
divisible par 3 quand les deux nombres ne le sont pas et quand les deux le
sont. |
4²
– 2² = 16 – 4 = 12 = 3 x 4 4²
– 3² = 16 – 9 = 7 5²
– 3² = 25 – 9 = 16 6²
– 3² = 36 – 9 = 27 = 3 x 9 7²
– 3² = 49 – 9 = 40 7²
– 4² = 49 – 16 = 33 = 3 x 11 |
|
|
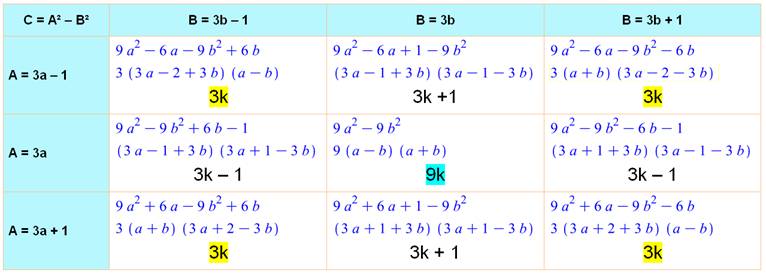
Explication: tableau des 3 x 3 cas possibles:
Les quatre cases d'angle correspondent à deux nombres
non divisibles par 3. |
||
|
3 Une telle expression est toujours
divisible par 3. |
En multipliant A² – B² par AB, nous transformons, les 1
des cases en croix en 3, ce qui rend toutes ces cases divisibles par 3. 4
x 2 (16 – 4) = 8 x 12 = 96 = 3 x 32 7
x 5 (49 – 25) = 35 x 24 = 3 x 8 x 35 |
|
|
|
|
|
Ces expressions sont premières pour le seul cas où p = 3.
|
|
|
|
||||
|
Un nombre n à trois chiffres dont ceux-ci sont en
progression
arithmétique, alors n est divisible par 3. |
n = 100a + 10b + c = 100a + 10(a + r) + (a + 2r) = 111a + 12r = 3 (37a + 4r) |
a = 4 & r = 2 => n = 468 a = 5 & r = 2 => n = 579 Valable même si les retenues interviennent: a = 6 & r = 2 => n = 690 |
||
|
Les seuls 16
nombres à trois chiffres à progression arithmétique |
[123, 234, 345, 456, 567, 678, 789] [135, 246, 357, 468, 579] [147, 258, 369] [159] |
|||
|
Généralisation à de plus
grands nombres. La relation est la même si le chiffre
a est remplacé par un nombre A. |
n = 100A + 10(A + r) + (a + 2r) = 3 (37A + 4r) Autre façon de voir: La somme des chiffres sera égale à: A+ A + r + A + 2r = 3A +
3r Elle est divisible par 3, le nombre l'est également. |
A = 7 & r = 3 => n = 100x7 + 10x10 + 13 =
813 A = 7 & r = 4 => n = 100x7 + 10x11 + 15 =
825 A = 45 & r = 12 => n = 100x45 + 10x57 + 69 = 5 139 |
||
|
|
||
|
Une puissance de 2 accolée (concaténée) à la
suivante forme un nombre divisible par 3. La même propriété
de divisibilité par trois se retrouve aussi pour:
Voir Brève
de math 491 |
Propriété
Exemple: 25
= 32 et 26 = 64. Le nombre 3264 est divisible par 3. Vrai aussi en
permutant: 6432 est divisible par 3. Démonstration Si la racine numérique de 2n est R, la
racine numérique de 2n+1 = 2 x 2n est 2 x R. La racine numérique de la concaténation est donc
3R. Ce qui montre que le tout st divisible par 3. Propriété
Exemple: 83 = 512 et 84 = 4096; le
nombre 5124096 est divisible par 9. |
|
|
|
|||
|
Démo rapide Sachant que 3 divise n3 – n (cas de trois nombres
successifs), on peut déduire => |
|
||
|
Démo par induction |
Pour n = 0: n3 + 2n = 0 qui est divisible par3 Confirmation avec n = 1: 13 + 2x1 = 3 qui est divisible par 3 Re-confirmation avec n = 2: 23 + 2x2 =
12 qui est divisible par 3 |
||
|
Hypothèse: il est vrai que
(n3 + 2n) est divisible par 3. |
Expression pour n = k + 1: (k + 1)3 + 2 (k + 1) = k3 +
3k2 + 3k + 1 + 2k + 2 = (k3 + 2k) + 3(k² + k + 1) Or, selon l'hypothèse (n3 + 2n) est
divisible par 3. Le second terme, avec le facteur 3, est divisible
par 3. Donc, toute l'expression est divisible par 3. Vraie pour 0 et vraie pour n+1 lorsque vraie pour
n, alors par induction,
vraie tout le temps ∎ |
||
Voir Brève de
Math 492
|
|
||
|
5n – 2n
est divisible par 3 pour tout nombre non-négatif |
||
|
|
50
– 20 = 3 Vrai. |
|
|
|
5k – 2k sont divisibles par 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Voir Démonstration
par induction
|
|
|||
|
3 Démonstration |
1
(2x 1 + 7) = 9 = 3 x 3 |
||
|
Validation du point de départ |
|||
|
|
f(1) |
= 2 + 7 |
|
|
Validation de la récurrence |
|||
|
|
f(n) |
= 3 .k |
|
|
|
f(n+1) |
= (n+1) ( 2(n+1)² + 7 ) = (n+1) (2n² + 4n + 9) = n (2n² + 4n + 9) + (2n² + 4n + 9) = 2n3 + 4n² + 9n +
2n² + 4n + 9 = 2n3 + 6n² + 13n + 9 |
|
|
|
f(n+1) – f(n) |
= 2n3 + 6n² + 13n + 9 – 2n3 –
7n + 9 =
6n² + 6n + 9 = 3 (2n² +
2n + 3) |
|
|
|
f(n) f(n+1) |
= 3 . k = 3 . h |
|
|
Conclusion |
|||
|
|
|||
Voir Démonstration
par induction
|
|
||
|
3 avec n>
0 |
n
= 1 => 22 + 5 = 9 = 3 x
3 n
= 2 => 24 + 5 =16 + 5 = 21 = 3 x 7 n
= 3 => 28 + 5 = 256 + 5 = 261 = 3 x 87 n
= 4 => 216 + 5 = 65 536 + 5 = 65 541 = 3 x 21 47 |
|
|
Rappel |
|
|
|
Calcul |
|
|
|
Modulo 3 |
||
|
Expression complète mod 3 |
(1
+5) |
|
|
Généralisation |
5 peut être remplacé par tout nombre de la
forme 3k + 2. Notamment 2. |
|
Voir Nombres de
Fermat
|
La
somme de ses achats s'écrit: 2
x 6 + 3 x (?) +
4 x 15 Chacun
des termes de la somme est divisible par 3; la somme doit l'être. Dans ce
cas, la somme des chiffres doit aussi être divisible par 3. Or 82 euros donne
8 + 2 = 10 non divisible par 3. Donc, erreur! |
Combien de nombres divisibles par 3 ?
|
Avec
les chiffres {0, 1, 2, 3, 4, 5} combien peut-on former de nombres à cinq
chiffres divisibles par 3? Tout
d'abord constatons que la somme de ces chiffres et égale à 15, nombre
divisible par 3. Les
seuls groupes de cinq nombres dont la somme est divisible par 3 sont: {1, 2,
3, 4, 5} et {0, 1, 2, 4, 5}. En
permutant les cinq chiffres
de {1, 2, 3, 4, 5}, il est possible de former 5!
= 120 nombres tous divisibles par 3. Avec
les cinq chiffres {0, 1, 2, 4, 5}, il
est possible de former 5! = 120 nombres tous divisibles par 3, sauf ceux
commençant par 0, soit 4! = 24. (il y a effectivement 4! nombres qui
commencent par chacun des cinq chiffres, ce qui donne 5 x 4! = 5! au total) Bilan:
120 + (120 – 24) = 216 nombres divisibles par 3. |
![]()
|
|
|||
|
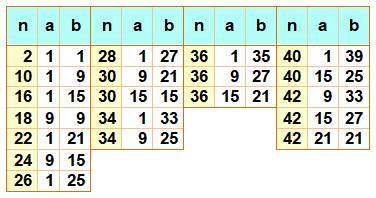
Affirmation Tout les
nombres pairs >38 sont la somme de deux nombres composés impairs. |
Exemples 40 = 1 + 39 = 15 + 25 42 = 9 + 33 = 15 + 27 = 21 + 21 |
||
|
Trois cas possibles n = 2m
avec m = 3k ou 3k +1 ou 3k + 2 Oui,
selon que le reste de la division par 3 est 0, 1 ou 2. Analysons
ces trois cas. |
42 = 2 x 21 = 2 x (3 x 7 + 0) 44 = 2 x 22 = 2 x (3 x 7 + 1) 46 = 2 x 23 = 2 x (3 x 7 + 2) |
||
|
Cas m = 3k => n = 6k On cherche
à trouver une relation équivalente avec une somme de deux termes dont chacun
est impair composé. On montre
que n = 12 ne peut pas être somme de deux composés impairs. |
Une somme de deux termes impairs: n = 6k = 3(2k – 1) + 3 Le premier terme est le produit de deux nombres impairs (3 et 2k – 1),
il est impair et composé. Le second est bien impair, mais il est premier. Poursuivons la recherche: n = 6k = 3(2k – 2) + 6 Pas de chance, 6 est pair. n = 6k = 3(2k – 3) + 9 Cette fois 9 est composé impair, c'est bon ! Quant au premier terme, il ne doit ni être négatif (k>1), ni
premier (k différent de 2). Soit k > 2 et donc n > 12. Avec 1 qui est impair sans être premier, on aurait 12 = 1 + 11 à
rejeter car 11 est premier. |
||
|
Cas m = 3k + 1 => n = 6k + 2 On
cherche à trouver une relation équivalente. On montre
que n = 38 ne peut pas être somme de deux composés impairs. |
n = 6k + 2 = 3(2k – 1) + 5 On a bien deux termes mais 5 est premier. On cherche les valeurs telles que le5 devienne un nombre composé impair. Il faut
aller jusqu'à: n = 6k + 2 = 3(2k – 11) + 35 Alors, pour éviter que le premier terme soit négatif ou premier, k
> 6 et n > 38. Avec 1 qui est impair sans être premier, on aurait 38 = 1 + 37 à
rejeter car 37 est premier. |
||
|
Cas m = 3k + 2 => n = 6k + 4 On
cherche à trouver une relation équivalente. On montre
que n = 38 ne peut pas être somme de deux composés impairs. |
n = 6k + 4 = 3(2k – 1) + 7 On a bien deux termes mais 7 est premier. Les valeurs qui conviennent: n = 6k + 4 = 3(2k – 7) + 25 Alors, pour éviter le cas du premier terme égal à 3, il faut rejeter k
= 4 et n = 28. Avec 1 qui est impair sans être premier, on aurait 28 = 1 + 27,
possible car 27 est composé. |
||
|
Bilan Après
le nombre 38, tous les nombres pairs sont somme de deux nombres composés
impairs |
Il est toujours possible de trouver une partition d'un nombre pair en
deux nombres composés impairs sauf pour n > 12, 28, 38, au final n >
38. Liste des nombres
pairs somme de deux impairs composés jusqu'à 42
|
||
Anglais: What is the maximum even number that cannot be
expressed as sum of two composite odd numbers?
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()