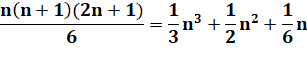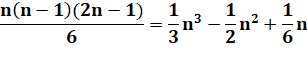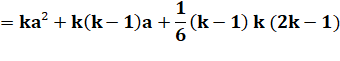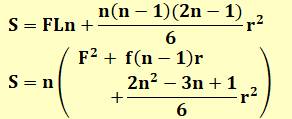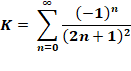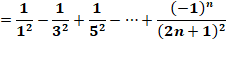|
||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES des CARRÉS avec nombres consécutifs |
|
|
||||
|
Carrés |
1² + 2² + … + n² |
|
||
|
1² + 2² + … + (n-1)² |
|
|||
|
À partir de a avec k termes |
a² + (a +
1)² + … + (a + k – 1)² |
|
||
|
Somme au carré |
(1
+ 2 + 3 + … + n )2 = 13 + 23 + 33 + … + n3 |
= { ½ n(n +1) } = Tn2 |
||
|
Pairs |
2²
+ 4² + 6² + … + (2n)² = 4 (1² + 2² + … + n²) |
= 2/3 n(n + 1)(2n + 1) |
||
|
Imp |
1² + 3² + 5² + … + (2n-1)² |
= 1/3 n(2n – 1)(2n
+ 1) = 1/3 n (4n² – 1) |
||
|
Carré en progression
arithmétique |
S = 5² + 11² + 17² + 23² = 964 F = 5 L= 23 = F + (n-1) r n = 4 r = 6 Voir Brève
534 |
|
||
Voir Somme de carrés et progression
géométrique
Trouvez les nombres consécutifs en
connaissant leur somme des carrés
|
Le
calculateur prodige Giacomo Inaudi
savait trouver en 30 secondes les quatre nombres consécutifs dont on donnait
la somme des carrés. Il procédait sans doute de cette manière: (24, 25,
26, 27) => 24² + 25² + 26² + 27² = 2 606 Diviser
par 4: 650 Produit de
deux nombres consécutifs: 650 = 25 x 26 Formule
utilisée: (n – 1)² + n² + (n + 1)² + (n + 2)² = 4n² + 4n + 6 = 4 n (n + 1) + 6 |
Voir Magie – Index / Brève de
maths n°234
|
Carrés - Inverses |
1/12 + 1/22 +
1/32 + … 1/n² + … = 2²/(2²-1) x 3²/(3²-1) x … x p²/(p²-1) x …
|
= = |
|
|
Inverses pairs |
1/22 + 1/42 +
1/62 … |
= |
|
|
Inverses imp |
1/12 + 1/32 +
1/52 … |
= |
|
|
Inverses opposés (somme) |
(1-1/2²) + (1-1/3²) + (1-1/4²) +… + (1-1/n²) + … |
|
|
|
Inverses opposés (produit) |
(1-1/2²) (1-1/3²) (1-1/4²) …
(1-1/n²) (1-1/2²) (1-1/3²) (1-1/4²) … |
= (n+2) / (2n+2) = 1/2 |
|
|
Inverse de produits |
3/(1².2²) + 5/(2².3²) + 7/(3².4²) +
… +
(2n+1)/(n².(n+1)² |
= (n² + 2n) / (n +
1)² = (A-1) / A avec A = (n+1)² |
|
|
Inverse de produits impairs |
12/(1.3) + 22/(3.5)
+ … n2/(2n-1)(2n+1) |
= n(n+1) / 2(2n+1) |
|
|
Inverse des carrés des impairs |
|
= 0,915 965 … |
|
|
ou Cumul
de la somme des carrés |
12
+ 12
+ 22 + 12
+ 22 + 32 + … |
S Ligne n
= 1/12 n (n+1)²
(n+2) Ex: N= 3 S = 20 |
|
|
Pyramide pairs carrés |
22 + (22 + 42 ) + (22 + 42 +
62 ) + … |
S Ligne n
= 1/3 n (n+1)
(n²+3n+2) Ex: N= 3 S = 80 |
|
|
Pyramide impairs carrés |
12 + (12 + 32 ) + (12 + 32 +
52 ) + … |
S Ligne n
= 1/6 n (n+1)
(2n²+2n-1) Ex: N= 3 S = 46 |
Voir Pyramide et nombres entiers
|
|
||
|
|
Voir Page spéciale |
|
|
|
2² + 4² + 6² + … + (2n)² = 4 (1² + 2² + … + n²) =
4/6 n (n + 1) (2n + 1) |
|
|
|
Somme des
entiers = 1² + 2² + … + n²
+ …
+ (2n)2 =
1/6 x 2n (2n + 1) ( 4n + 1) Somme des
pairs = 2² + 4² + 6² +
… + (2n)² =
2/3 n (n + 1) (2n + 1) Somme des
impairs = 1² + 3² + 5² + … +
(2n-1)² =
1/6 x 2n (2n + 1) (4n + 1) –
{2/3 n (n + 1) (2n + 1)} =
n/3 (4n² – 1) |
|
|
|
||
|
|
= 2n² + 2n + 1 La somme des carrés de deux nombres
consécutifs peut être un nombre premier
(pour les 1000 premiers nombres, il y 225 premiers). Voici les 5 premières
configurations: 1²
+ 2² = 5 2²
+ 3² = 13 4²
+ 5² = 41 5²
+ 6² = 61 7²
+ 8² = 113 |
|
|
|
= 3n² + 2 La somme des carrés de deux nombres
consécutifs peut être un nombre premier (pour les 1000 premiers, il y 83
premiers). Voici les 5 premières configurations: 2² +
3² + 4² = 29 6² +
7² + 8² = 149 12²
+ 13² + 14² = 509 14²
+ 15² + 16² = 677 24² + 25² + 26² = 1877 |
|
|
Toujours pair |
= 2 (2n²
+ 6n + 7) 1²
+ 2² + 3² + 4² = 30 2²
+ 3² + 4² + 5² = 54 3² + 4² + 5² + 6² = 86 |
|
|
|
= = 5 (n²
+ 2) 1²
+ 2² + 3² + 4² + 5² = 55 = 5 x 11 2²
+ 3² + 4² + 5² + 6² = 90 = 5 x 18 3²
+ 4² + 5² + 6² + 7² = 135 = 5 x 27 |
|
Voir Somme
des carrés de nombres consécutifs
|
|
||||
|
|
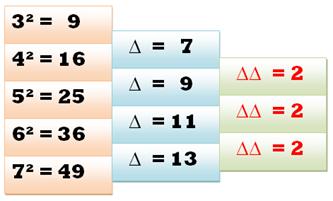
= 2n + 1 |
Pour passer au carré suivant il
suffit d'ajouter deux fois le nombre plus un. |
||
|
|
= 2 |
L'écart entre la différence des carrés successifs est toujours égal à 2. |
||
|
|
= 6 |
6²
– 5 ² – 3² + 2² = 6 7²
– 6 ² – 4² + 3² = 6 8²
– 7 ² – 5² + 4² = 6 |
||
Voir Machine de Babbage
![]()
|
Suite |
|
|
Table |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomCarre.htm |
![]()