Glossaire - nombres géométriques

NOMBRES FIGURÉS

ou nombres géométriques

ou nombres polygonaux, polyédraux …

Sommaire de cette page

>>> Définition et exemples

>>> Grandes familles

>>> Gnomon

>>> Liste des nombres figurés, formules, exemples et liens

>>> Anglais

*Définition*	Nombres figurés Nombres associés à des figures géométriques. Quantité de points (pions, cailloux, éléments …) entrant dans la composition d'une figure géométrique. Nombre géométriques Autre nom pour nombres figurés. Nombres polygonaux Nombre figuré avec une forme de polygone régulier.
*Exemples*	Dans un plan: polygonaux		Dans l'espace: polyédraux
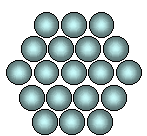
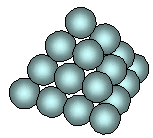
*Exemples*	Triangulaire – 10 10 = 1 + 2 + 3 + 4	Hex – 19 ou hexagonal centré 19 = 1 + 6 + 12	Tétraédral – 20 ou pyramide à base triangle 20 = 1 + 3 + 6 + 10

Types

Divers types de nombres géométriques:

oblongs, triangulaires, carrés, pentagonaux …

cube, tétraédraux, pyramide …

généralisés.

Aussi, selon la dimension de la figure géométrique

nombres linéaires;

nombres plans:

nombres plan polygonaux:

triangulaires, carrés , hexagonaux …

nombres rectangles, nombres oblongs , n gnomons.

nombres plan polygonaux centrés;

nombres solides:

nombres pyramidaux,

nombres tétraédriques.

nombres hypersolides.

Origine

Les nombres figurés, représentés par des points disposés selon des figures géométriques ont été étudiés dès l’Antiquité. Idée de lier l'arithmétique à la géométrie.

Les Grecs avaient hérités leurs nombres des géomètres égyptiens. Il n'y avait pas de distinction entre les figures et les nombres.

Pour les philosophes, c'était la même chose.

Pour Pythagore et son école "tout est nombre". Pour eux, le lien entre les figures et les nombres est profond et mystérieux. Chaque forme de nombre a un sens caché, et les plus belles étaient sacrées. L’arithmétique pythagoricienne est géométrique, elle classe les nombres selon la forme des assemblages correspondants, et elle est visuelle car de nombreuses propriétés sont directement visibles sur les représentations.

Diophante a résolu plusieurs problèmes les concernant. Pascal a écrit un traité sur le sujet.

Ce sujet a passionné: Cardan, Bachet de Méziriac, Descartes, Fermat, Pell, Pascal, Euler, Lagrange, Legendre, Gauss, Cauchy, Jacobi, Sierpinski, Wallis et de nombreux mathématiciens plus contemporains.

Leurs études ont parfois donné lieu à des développements très complexes. Il est vrai que les représentations figurées permettent souvent de visualiser certaines propriétés des nombres. Notamment les relations entre eux et avec les coefficients binomiaux, les triplets de Pythagore, les nombres parfaits, ceux de Fibonacci ou de Lucas …

Gnomon

Quantité qu'il faut ajouter à une figure pour obtenir la figure suivante.

Exemple pour passer du carré 2x2 au carré 3x3 il faut ajouter le gnomon 5 et pour passer au carré suivant 4x4, il faudra ajouter 7;

d'où la propriété avec les nombres impairs:

1 + 3 + 5 + 7 + … + (2n-1) = n².

Anglais

Figurate numbers or Polygonal numbers (Old name: figural numbers).

Such numbers represent an ancient link between geometry and number theory.

Their origins can be traced back to the Greeks,

where properties of oblong, triangular, and square numbers

were investigated and discussed

by the sixth century BC, pre-Socratic philosopher Pythagoras of Samos and his followers.

Orientation

Ce site comporte de nombreux développements sur les nombres figurés

Ce sont les premiers éléments de réflexion historique sur la théorie des nombres

Ils sont également une source de découvertes et d'amusements

Les notions sont très facilement abordables

Directions possibles

Glossaire

Définition générale

et orientations

Introduction

Pour commencer

en douceur

Qui sont-ils ?

Valeurs, calcul, propriétés

Un par un

Nomenclature

La théorie

Les démonstrations

Carrés

Cubes

Tables des nombres géométriques

INDEX

Général

Par type

Généralité sus les nombres figurés

>>> Débutants

>>> Utilité

>>> Historique

>>> Figurés, polygonaux, polyédraux …

>>> Propriétés – Progression arithmétique, produits en croix

>>> Formules de calcul

>>> Tables pour F_n de 1 à 10

>>> Table des nombres de 1 à 25 et leurs caractéristiques géométriques

>>> Nombres figurés – Théorèmes

Nombres polygonaux

>>> Nom des polygones

>>> Images de construction des polygonaux (3 à 8)

>>> Formules de calcul (3 à 8)

>>> Nombres polygonaux centrés – Triangle, carré et cube

Images / illustrations

>>> Nombres polygonaux (débutants)

>>> Nombres polygonaux

>>> Nombres polygonaux simples

>>> Nombres polygonaux centrés

>>> Nombres figurés (exemples)

Nombres impairs ou nombres en L ou gnomons

>>> Images des six premiers

Nombres rectangulaires (composés) et nombres premiers (linéaires)

>>> Images des six premiers

Nombres proniques ou oblongs ou hétéromèques

>>> Images des six premiers

>>> Oblongs et pairs

Nombres triangulaires

>>> Images des cinq premiers et somme des entiers

>>> Triangulaires et oblongs

>>> Triangulaires centrés

Nombres carrés ou nombres losanges ou triangulaires centrés

>>> Images des six premiers

>>> Nombres triangles – Développements

>>> Carrés et impairs

>>> Carrés et triangulaires

>>> Carrés centrés

Nombres pentagonaux

>>> Grappe pentagonale

Nombres cubes

>>> Cubes centrés

Les principaux polygonaux (k-gonaux)
2D	Poly	Poly centrés	Triangle 3-gonal	Carré 4-gonal	Penta 5-gonal	Hexa 6-gonal
	Hepta 7-gonal	Octa 8-gonal	Ennéa 9-gonal	Déca 10-gonal	Grappe	Étoilé
3D et +	Polyédraux	Cubes	Tétraédriques	Octaédriques	Icosaédraux	Dodécaédraux
	Pyramidaux					L-gonaux
Autres	Polytopes	Pentatopes	P. Carrée Triangle

Accès aux nombres ordinaires, du deuxième ordre, généralisés, centrés … avec les liens ci-dessus

Liste des types de nombres figurés

Voir aussi Nombres figurés – Index

Nombres figurés Figurate numbers	Formule Les 10 premiers
Bicarré, biquadratique (puissance 4) biquadratic numbers	1, 16, 81, 256, 625, 1296, 2401, 4096, 6561, 10000	>>>
Carré square number	1, 4, 9, 16, 25, 36, 49, 64, 81, 100	>>>
Carré …	Carré centré / Carré-carré / Carrément carré Doublement carré / Triangulaire carré
Carré centré centered square number	1, 5, 13, 25, 41, 61, 85, 113, 145, 181
Cube cubic number	1, 8, 27, 64, 125, 216, 343, 512, 729, 1000	>>>
Cube centré centered cube number	1, 9, 35, 91, 189, 341, 559, 855, 1241, 1729
Cube doublement	1, 8, 125, 512, 1000, 1331	>>>
Décagonal (10-gonal) decagonal number	1, 10, 27, 52, 85, 126, 175, 232, 297, 370	>>>
Décagonal centré centered decagonal number	5n² – 5n + 1 1, 11, 31, 61, 101, 151, 211, 281, 361, 451,	>>>
Dodécagonal (12-gonal) dodecagonal number	1, 12, 33, 64, 105, 156, 217, 288, 369, 460	>>>
Dodécagonal centré centered dodecagonal number	6n² – 6n + 1 1, 13, 37, 73, 121, 181, 253, 337, 433, 541	>>>
Dodécaédrique rhombique Rhombic dodecahedral number	(2n – 1)(2n² – 2n + 1) 1, 15, 65, 175, 369, 671, 1105, 1695, 2465, 3439
Dodécaèdre rhombique de Haüy Haűy rhombic dodecahedral number	1, 33, 185, 553, 1233, 2321, 3913, 6105, 8993, 12673
Ennéagonal (9-gonal) Nonagonal number	1, 9, 24, 46, 75, 111, 154, 204, 261, 325	>>>
Ennéagonal centré Centered nonagonal number	1, 10, 28, 55, 91, 136, 190, 253, 325, 406	>>>
Étoilé	6n(n – 1) + 1 1, 13, 37, 73, 121, 181, 253, 337, 433, 541	>>>
Hendécagonal (11-gonal) hendecagonal number	1, 11, 30, 58, 95, 141, 196, 260, 333, 415	>>>
Heptagonal heptagonal number	1, 7, 18, 34, 55, 81, 112, 148, 189, 235	>>>
Heptagonal centré ou Pentagonal en grappe centered heptagonal number	8, 22, 43, 71, 106, 148, 197, 253, 316	>>>
Hex (nombre -) ou hexagonal centré hex number	7, 19, 37, 61, 91, 127, 169, 217, 271, 331	>>>
Hexagonal hexagonal number	1, 6, 15, 28, 45, 66, 91, 120, 153, 190	>>>
Hexagonal du deuxième ordre second hexagonal number	0, 3, 10, 21, 36, 55, 78, 105	>>>
Hexagonal centré centered hexagonal number	Voir Hex
Impair ou gnomon odd number or gnomonic number	1, 3, 5, 7, 9, 11, 13, 15, 17, 19	>>>
Linéaire	Suite arithmétique de nombres dont les gnomons.	>>>
Multiplicatifs	Images de la multiplication.	>>>
Multi-polygonaux	Plusieurs présentations polygonales.	>>>
Nexus (Nombre -) Nexus number
Octaédrique octahedral number	1, 6, 19, 44, 85, 146, 231, 344, 489, 670	>>>
Octaédrique centré ou de Haüy Haűy octahedral number	1, 7, 25, 63, 129, 231, 377, 575, 833, 1159	>>>
Octaédriquel tronqué truncated octahedral number	1, 38, 201, 586, 1289, 2406, 4033, 6266, 9201, 12934
Octogonal octagonal number	1, 8, 21, 40, 65, 96, 133, 176, 225, 280	>>>
Pair even numbers	2, 4, 6, 8, 10, 12, 14, 16, 18, 20	>>>
Pentagonal pentagonal number	1, 5, 12, 22, 35, 51, 70, 92, 117, 145	>>>
Pentagonal centré centered pentagonal number	6, 16, 31, 51, 76, 106, 141, 181, 226, 276	>>>
Pentagonal du deuxième ordre second pentagonal number	2, 7, 15, 26, 40, 57, 77, 100, 126, 155	>>>
Pentagonal généralisé pentagonal number	0, 1, 2, 5, 7, 12, 15, 22, 26, 35	>>>
Pentagonal en grappe	1, 8, 22, 43, 71, 106, 148, 197	>>>
Pentatope (Nombre -) pentatope number	1, 5, 15, 35, 70, 126, 210, 330, 495, 715
Polygonal polygonal number		>>>
Polygonal centré centred polygonal number		>>>
Pronique ou oblong ou hétéromécique pronic number	2, 6, 12, 20, 30, 42, 56, 72, 90, 110	>>>
Pyramidal triangle	Voir Tétraédrique
Pyramidal carré square pyramidal number	1, 5, 14, 30, 55, 91, 140, 204, 285, 385	>>>
Pyramidal hexagone hexagonal pyramidal number	1, 7, 22, 50, 95, 161, 252, 372, 525, 715
Pyramidal pentagone pentagonal pyramidal number	1, 6, 18, 40, 75, 126, 196, 288, 405, 550
Pyramidal heptagone heptagonal pyramidal number	1, 8, 26, 60, 115, 196, 308, 456, 645, 880
Pyramidal octogone octagonal pyramidal number	1, 9, 30, 70, 135, 231, 364, 540, 765, 1045	>>>
Octaédrique octahedral number	1, 6, 19, 44, 85, 146, 231, 344, 489, 670	>>>
Rectangle ou nombres produits	4, 6, 8, 9, 10, 12, 15, 16, 20, 25	>>>
Rectangle ou nombres proniques Rectangular numbers	Voir Pronique
Stella octangle stella octangula number	1, 14, 51, 124, 245, 426, 679, 1016, 1449, 1990
Tétraédriques (pyramidal triangle) tetrahedral number	1, 4, 10, 20, 35, 56, 84, 120, 165, 220	>>>
Tétraèdre tronqué truncated tetrahedral number	1, 16, 68, 180, 375, 676, 1106, 1688, 2445, 3400
Triangulaire triangular number	1, 3, 6, 10, 15, 21, 28, 36, 45, 55	>>>
Triangulaire centré centered triangular number	1, 4, 10, 19, 31, 46, 64, 85, 109, 136	>>>

Voir Tables

Retour	Géométrie – Glossaire
Suite	Hauteur – Glossaire
En savoir plus	Nombres figurés – Index Tous les noms des nombres et familles de nombres par ordre alphabétique Domaines mathématiques Géométrie - Glossaire Géométrie – Index
Sites	Les nombres polygonaux et la généralisation – André Ross – pdf 26 pages Figurate numbers d'Eric Weisstein
Livres	Le livre des nombres ou The book of numbers – Conway et Guy
Cette page	http://villemin.gerard.free.fr/Referenc/Vocabula/GlosG/Geonombr.htm