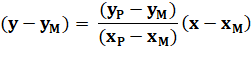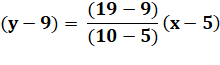dérivées faciles via les nombres

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/04/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ANALYSE
Débutants Général	Dérivées			Glossaire Dérivée
INDEX Analyse	Approche	Débutants	Développement
	Intérêt des dérivées	Ficelles de première	Les dérivées
		Exemples résolus	Exemples (limites)
		Sommaire de cette page >>> Progression des carrés des nombres >>> Progression des cubes des nombres

DÉRIVÉE – Débutants

Approche via le carré et le cube des nombres

Vous avez le sentiment de ce à quoi sert une dérivée.

Voyons une approche simple plus mathématique qui vous permettra de mieux cerner ce que veut dire une dérivée en pratique.

Coucou! Je suis en première et je voudrais démarrer d'un bon pas >>>

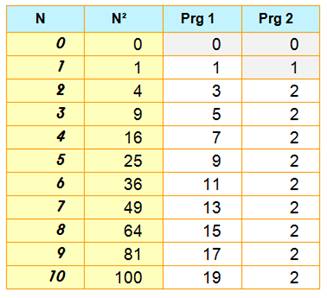
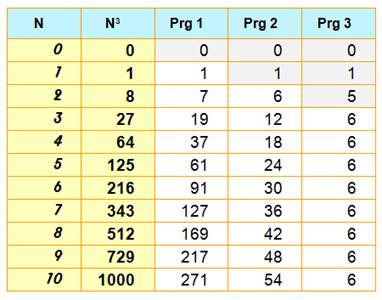
Progression des carrés des nombres
Nous nous intéressons aux carrés des nombres entiers. Et plus particulièrement à la vitesse de leur progression. La colonne Prg 1 du tableau montre l'écart pour passer d'un carré au suivant, le pas de progression; la marche à monter. Cet écart est régulier: c'est la suite des nombres impairs et l'écart entre eux (colonne Prg 2) est égal à deux. La courbe qui représente les carrés est une parabole du type y = x². Ici, tout simplement: C = N².	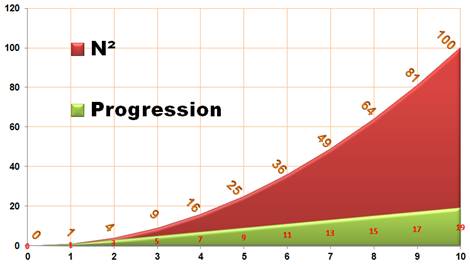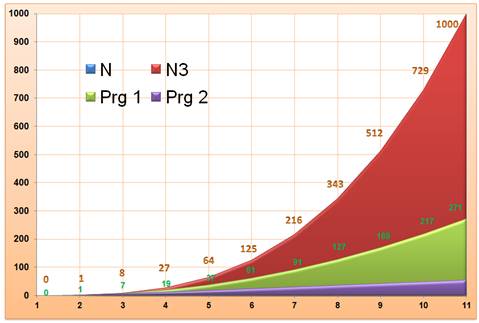Table de progression des carrés Courbe de progression des carrés
La courbe qui représente la progression des carrés est une droite. On note deux points: M: x = 5 y = 9 P: x = 10 y = 19	y = 2x – 10 + 9 y = 2x – 1

Bilan sur les carrés

Les carrés des nombres sont en x², une parabole.

Leur progression est en 2x, une droite.

fOn dit que la dérivée (le taux de progression) de x² est 2x.

Notez l'arrivée du coefficient 2 alors que nous parlons de carrés.

Quantités arbitrairement petites

Prenons l'exemple de la courbe: y = x².

Comparons la courbe en deux points proches:

- écart en abscisse: d (un petit accroissement)

- écart en ordonnée: D = (x + d)² – x² = x² + 2xd + d² – x² = d (2x + d)

- soit le rapport entre les deux: p = 2x + d

Pour d tendant vers 0, le rapport p s'approche de 2x

La dérivée de x² est 2x.

Progression des cubes des nombres
Nous nous intéressons aux cubes des nombres entiers. Et plus particulièrement à la vitesse de leur progression. La colonne Prg 1 du tableau montre l'écart pour passer d'un cube au suivant. Cet écart (Prg 1) ne semble pas régulier. Par contre, sa propre progression (Prg 2) est régulière (+6). C'est une progression linéaire. AhAh! Intuition! Nous venons juste de voir qu'une progression linéaire provient d'une parabole, d'une courbe en x². Ce qui nous laisserait penser que les cubes (en x³) progresserait en x². Vérifions cela.	Table de progression des cubes Courbe de progression des carrés
Prenons trois points sur la courbe de progression des cubes (la verte ou tableau en Prg 1).	M: x = 3 y = 19 P: x = 6 y = 91 Q: x = 10 y = 271
Équation de la parole passant par ces trois points	y = ax² + bx + c 19 = 3²a + 3b + c (1) 91 = 6²a + 6b + c (2) 271 = 10²a + 10b + c (3)
Faisons (2) – (1)	27a + 3 b = 72 9a + b = 24 (4)
Faisons (3) – (1)	91a + 7b = 252 13a + b = 36 (5)
Faisons (5) – (4)	4a = 12 a = 12 / 4 = 3
Valeurs de b	9 x 3 + b = 24 b = 24 – 27 = – 3
Et de c	19 = 9 x 3 – 3 x 3 + c 19 = 27 – 9 + c = 18 + c c = 19 – 18 = 1
Équation de la parabole	y = 3x² – 3x + 1