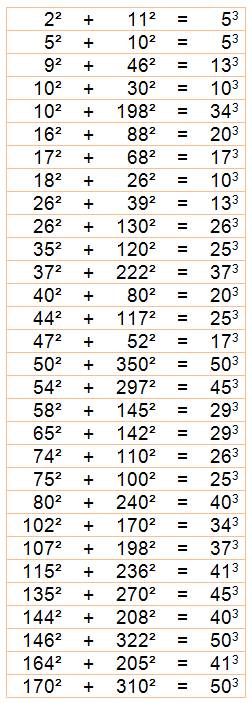|
||||||||||||
![]()
|
PARTITION et DIVISIBILITÉ Avec les carrés Un ou plusieurs carrés. Et, même des cubes … |
|
|
||
|
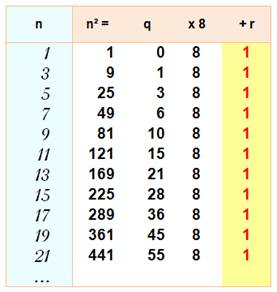
Nombres
pairs
Exemple 12²
= 144 et 144 = 8 x 16
Exemple 10²
= 100 et 100 = 4 x 25 Conclusion Le carré d'un nombre pair, divisé par 8, laisse un reste de 0
ou 4. |
(2k
+ 1)² = 4k² + k + 1 = 4k (k+1) + 1
Conclusion Le carré d'un nombre impair, divisé par 8, laisse un reste de 1. Le
carré d'un nombre impair est un multiple de 8 plus 1. Exemples
|
|
Petite récréation à propos de 8 et
généralisation.
|
Je
souhaite que n divise n + 8. Est-ce possible? Je
dis que n divise n et n + 8, il divise une combinaison linéaire de des deux
nombres, seule condition, les coefficients doivent être entiers. Je les
choisis de façon à faire disparaître n: (-1) x n + (1) x (n + 8) = n – n +
8 = 8 Bilan:
n divise n + 8 si n divise 8 et, n = {1, 2, 4, 8} Réciproquement:
n divise 8 et n, alors n divise leur somme: n + 8. On
se serait douté du résultat: n divise n + 8 s'il divise chacun des termes.
Pour n c'est le cas, reste 8. D'où le fait que n doit diviser 8. On
peut remplacer 8 par k et avoir la condition générale: pour que n divise n + k, il faut que n divise k. |
|
|
|
|
Somme
pour n et m < 10 et divisibilité par 4 n m n² + m² (n² + m²) mod 4 1 1 2 2 1 2 5 1 2 2 8 0 1 3 10 2 2 3 13 1 1 4 17 1 3 3 18 2 2 4 20 0 3 4 25 1 1 5 26 2 2 5 29 1 4 4 32 0 3 5 34 2 1 6 37 1 2 6 40 0 4 5 41 1 3 6 45 1 1 7 50 2 5 5 50 2 4 6 52 0 2 7 53 1 3 7 58 2 5 6 61 1 1 8 65 1 4 7 65 1 2 8 68 0 6 6 72 0 3 8 73 1 5 7 74 2 4 8 80 0 1 9 82 2 2 9 85 1 6 7 85 1 5 8 89 1 3 9 90 2 4 9 97 1 7 7 98 2 6 8 100 0 1 10 101 1 2 10 104 0 5 9 106 2 3 10 109 1 7 8 113 1 4 10 116 0 6 9 117 1 5 10 125 1 8 8 128 0 7 9 130 2 6 10 136 0 8 9 145 1 7 10 149 1 9 9 162 2 8 10 164 0 9 10 181 1 10 10 200 0 Remarques liminaires
|
|
Voir Sommes de deux carrés deux fois
|
Conclusions Le reste de la
division par 4 de n² +
m² est toujours 0, 1 ou 2. Mais
jamais 3. Un nombre en 4k + 3
n'est pas décomposable en somme
de deux carrés. 5 13 17 37 39 41 53 ...
Exemples avec mod 2 à 5 n m n² + m² mod
2 mod
3 mod
4 mod
5 5 5 50 0 2 2 0 5 6 61 1 1 1 1 5 7 74 0 2 2 4 5 8 89 1 2 1 4 5 9 106 0 1 2 1 5 10 125 1 2 1 0 6 6 72 0 0 0 2 6 7 85 1 1 1 0 6 8 100 0 1 0 0 6 9 117 1 0 1 2 6 10 136 0 1 0 1 7 7 98 0 2 2 3 7 8 113 1 2 1 3 7 9 130 0 1 2 0 7 10 149 1 2 1 4 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Cas
des nombres premiers Un nombre premier est la somme de 2 carrés si p + 1
n'est pas divisible par 4 et, la somme est unique. Tout nombre premier de la forme 4n + 1 est la somme unique de deux carrés. Trouvé par
Fermat,
démontré par Euler Valeurs pour n < 50
Cas
d'un nombre quelconque Un nombre est la somme de 2 carrés si aucun de ses facteurs + 1 n'est pas divisible par 4.
La somme n'est pas forcément unique. Exemples
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Explications
théoriques / Somme de deux carrés et utilisation
des nombres complexes
|
|
|
|
Exemples 0 0 1 = 1 0 0 4 = 4 0 1 1 = 2 0 1 4 = 5 0 4 1 = 5 0 4 4 = 8 1 0 1 = 1 1 0 4 = 4 1 1 1 = 3 1 1 4 = 6 1 4 1 = 6 1 4 4 = 9 4 0 1 = 5 4 0 4 = 8 4 1 1 = 6 4 1 4 = 9 4 4 1 = 9 4 4 4 = 16
Un nombre dont la division par 8 donne un reste de 7
n'est pas la somme de trois carrés. 7,
15, 23, 31, 39, 47, 55, 60 ... ne sont pas la somme de 3 carrés. Théorème
de Gauss N est somme de trois carrés au plus
(N = A² + B² + C²) si et seulement si N Tout entier est décomposable en
somme d'au plus quatre carrés: N = A² + B² +
C² + D². Voir Théorème de Lagrange / quaternions |
|
|
|
|||||||||||||||||||
|
Somme
de carrés distincts Si n est supérieur à 128, il peut être
décomposé en une somme de carrés tous distincts. 128:
Plus petit non décomposable 129
= 4² + 7² + 8² Somme
de carrés de premiers distincts Tous les nombres, au-delà de 17 163, sont
la somme de deux premiers distincts au carré. Carré,
somme de 2 cubes Exemple 13
+ 23 = 32 703
+ 1053 = 1 2252 Construction Prendre
2 nombres (exemple 2 & 3) et procéder comme suit: 23
+ 33 = 8 + 27 = 35 Multiplier
par le résultat au cube: 353 (2x35)3
+ (3x35)3 = 35x353 = (35²)2 703 +
1053 = 1 2252 Cube,
somme de 2 carrés par construction Exemple 5²
+ 10² = 53 26²
+ 39² = 133 Construction Prendre
2 nombres (exemple 2 & 3) et procéder comme suit: 2²
+ 3² = 4 + 9 = 13 Multiplier
par le résultat au cube: 132 (2x13)2
+ (3x13)2 = 13x132 = 133 26²
+ 39² = 133 676
+ 1 521 = 2 197
Voir Équation E223 Carré,
somme de trois carrés 81 est le plus petit carré
décomposable en somme de trois carrés. 81
= 9² = 1² + 4² + 8² Nombre,
2 fois somme de deux carrés Les nombres, somme de deux carrés de deux
façons sont: 50, 65, 85, 125, 130, 145... 50 = 5²
+ 5² = 1² + 7² 65 = 7²
+ 4² = 1² + 8² 85 = 9²
+ 2² = 7² + 6² Carré,
somme de deux carrés (Pythagore) Il existe une infinité de triangles de Pythagore dont l'hypoténuse
et un côté diffèrent de l'unité. Ils
suivent le motif suivant: 3² = 9 = 4 +
5 => 3² +
4² = 5² 5² = 25 =
12 + 13 5² + 12² = 13² 7² = 49 =
24 + 25 7² + 24² = 25² etc. Il
en existe une infinité d'autres dont la construction n'est pas aussi simple. Le produit de deux nombres qui sont
chacun la somme de deux carrés, est également la somme de deux carrés. (1 + 4) (9 + 16) = 125 = 100 + 25 = 10² +
5² Carré,
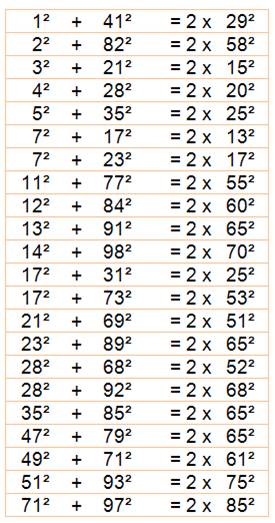
somme de la moitié de deux carrés Tous les triplets a² + b² = 2c² pour c
jusqu'à 100.
Carré,
somme des impairs Tout carré est la somme des nombres
impairs successifs 1 + 3 + 5 + 7 + 9 = 25 = 5 ² Carré,
somme de nombres triangulaires Tout nombre carré est décomposable en
somme de deux nombres triangulaires successifs. Tout carré impair est égal à 8 fois un
nombre triangulaire, plus un. Le carré de tout nombre impair est égal à
la différence entre deux nombres triangulaires premiers entre eux. Il existe une infinité de carrés tels
qu'ils soient le produit de deux nombres triangulaires. Carré,
somme symétrique
|
|||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Théorème Tout nombre de la forme 4n + 2
n'est pas décomposable en différence de deux carrés. 2, 6, 10, 14, 18 … Différences particulières
Généralisation
On peut continuer avec 1001, 10001, etc. |
||||||||||||||||||||||||||||||||||||||||||
Voir Nombre 784
|
|
||
|
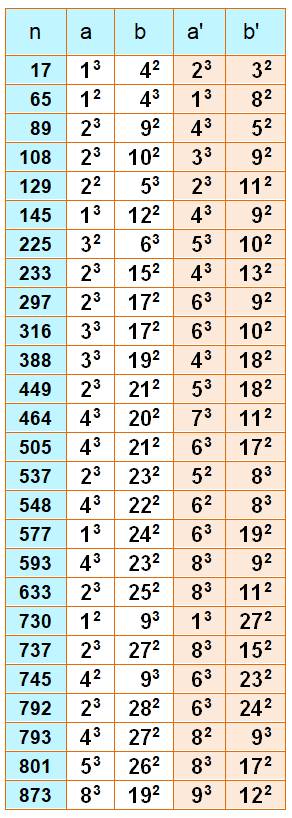
Nombres
qui sont somme d'un carré et d'un cube et cela deux fois. Exemple 108 = 23
+ 102 = 33 + 92 =
8 + 100 = 27 + 81 Voir suite avec somme carré
et cubes k fois |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()