![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et pour cette page voir
le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
SUITE
ARITHMÉTIQUE ou PROGRESSION
ARITHMÉTIQUE C ou séparés par le
même écart. La somme est
nommée: série arithmétique. Curiosité: premier cas de progression arithmétique entre
carrés
Voir Carrés en progression
/ Pépite / Nombre 24 |
Anglais: Arithmetic
progression, common difference
Voir
Moyenne arithmétique / Suite et Série
|
|
|
|
Pensez à: Dans la troposphère
la température diminue à raison de 5 à 6degrés par kilomètre. |
|
|
NOMBRES CONSÉCUTIFS |
|
||||||||||||
|
Astuce
de calcul
Méthode
générale 1
+ 2 + 3 + ... + n = n ( n + 1 ) / 2 Ce sont les nombres triangulaires |
|||||||||||||
Voir
Somme de 1 à 100 et
Gauss / Méthode de calcul et démonstration / Carrés magiques
|
|
||
|
Somme |
Produit |
|
|
T = 1 + 2 + 3 +...+ n = n (n + 1) / 2 |
F = 1 x 2 x 3 x...x n = = n! |
|
|
|
||
|
Somme
de n nombres successifs Méthode
adaptée aux quantités |
||
|
n impair |
n pair |
|
|
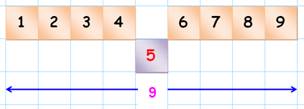
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 S = 5 x 9 =
45 |
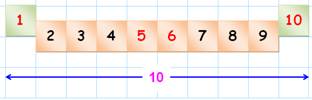
1 + 2 + 3 + 4 + 5 + 6 +
7 + 8 + 9 + 10 = 55 S = (1 + 10)
x 10 / 2 = 55 |
|
|
S = Milieu x Quantité
n de nombres |
S = Somme extrémités x
Demi-quantité des nombres |
|
|
|
= 11
+ 11 +
11 + 11
+ 11
|
|
|
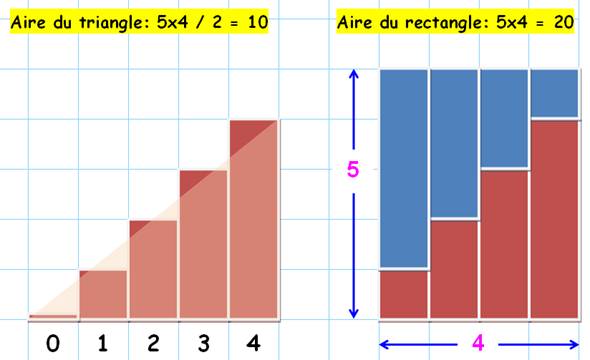
Illustration
|
||
Voir Triangle rectangle / Rectangle
|
|
||
|
Généralisation
|
||
|
S = Milieu x Quantité n de nombres |
S = Somme
extrémités x Demi-quantité des nombres |
|
|
A = 3 + 6
+ 9 + 12 + 15 Milieu = 9 Quantité =
5 A = 9 x 5
= 45
|
A = 3 + 6
+ 9 + 12 + 15 Extrémités
= 3 et 15 Leur somme
= 18 Demi
quantité = 5 / 2 A = 18 x 5
/ 2 = 45
|
|
|
|
|||||||||||||||||||||||
|
Formules
générales
Exemple 10, 13, 16, 19, 22 n = 5 a = 10; b = 21 r = 13 – 10 = 3; r = (22 – 10) / 4 =12/4 = 3 S = (10 + 22) x 5 / 2 =
32 x 5 / 2 = 16 x 5 = 80 Nombres impairs successifs 1, 3, 5, 7, 9, 11 a = 1; b = 11 S = (1 + 11) x 6 / 2 = 12
x 3 = 36 = 6² Calcul
sans impliquer le dernier terme
S = (a + b) . n / 2
b = a + (n – 1) r
S = ½ (an + an + (n – 1)r n) = an + (n – 1)n r S = a . n + ½ r
. n (n – 1) |
|||||||||||||||||||||||
Voir Somme des entiers, des impairs …
/ Vraie anecdote concernant Gauss
|
|
||
|
|
La
nouvelle suite de nombres est une PA. |
|
|
|
La
nouvelle suite de nombres est une PA. |
|
|
|
La
nouvelle séquence de nombres est une PA |
|
|
Une solution passe par l'étude de la forme
elliptique d'équation: Voir Sites en référence Note: Avec
trois, il y en a une infinité: Par exemple, 24 est différence
de carrés deux fois : 7² – 5² = 5² – 1² =
24 |
||
|
|
||
|
10 + 20 + 30 + 40 + 50 |
Méthode
premier-dernier S = (10 + 50) x 5/2 = 30 x 5 = 150 Méthode
premier-quantité S = 10 x 5 + ½ x 10 x 5 x 4 =
50 + 100 = 150 |
|
|
5,5 + 6,75 + 8 + … 20
termes |
S = 5,5 x 20 + ½ (1,25 x 20 x
19) = 347,5 |
|
|
Une
PA 5 + … + 45 = 400 Quantité
et raison? |
Quantité
de termes 400 = (5 +
45) x n / 2 n = 800 /
50 = 16 Raison
de la PA (progression arithmétique) 45 = 5 +
(16 – 1) r r = 40 /
15 = 8 / 3 = 2,666… |
|
|
Une
PA de 22 termes: 4 + … + 67 Lister
les termes |
67 = 4 +
21 r => r = 63 / 21 = 3 4 + 7 + 10
+ … + 61 + 64 + 67 |
|
|
Une
PA avec le 4e et le 54e termes connus: … + 644
+ … – 6154 + … Quelle
est la raison? |
Deux
équations 64 = a + 3r –61 = a +
53 r Résolution 64 + 61 =
(3 – 53) r r = –125 /
50 = –2,5 |
|
|
Trouver
trois nombres en PA dont la somme est 27 et dont la somme de leur carré est
293 |
Valeur
du nombre central (m – r) +
m + (m + r) = 3m = 27 m = 9 9² + (9 +
r)² = 243 + 2r² = 293 r² = 50 /
2 = 25 r = 5 Suite
arithmétique 4, 9, 14 |
|
|
Une
AP de somme 66: – 9, –6, –3, … Combien
de termes ? |
Équation 66 = (–9)
x n + ½ x 3 x n (n – 1) 66 = ½ (3 n² – 21 n) (n + 4)(n
– 11) = 0 n = –4 ou
+11 Solution
avec 11 termes – 9, –6,
–3, 0, 3, 6, 9, 12, 15, 18, 21 |
|
|
|
||
|
Euler (1972) Suite la plus connue en n²
+ n + 41. |
Cette formule pour n de 0 = 39 produit une suite
de nombres
premiers en progression arithmétique. |
|
|
Dirichlet (preuve en 1838) On note
p(a, d) = p(41, 40) Avec (a, d) = 1 a est le premier nombre premier, et d est la quantité de nombres premiers successifs. |
Il en existe d'autres. Le théorème de Dirichlet dit même
qu'il existe une infinité de nombres premiers de la forme an + d avec a
et d premiers entre eux. Autrement dit: il existe une infinité de nombres
premiers congruent à a modulo d. |
|
|
Linnik (preuve en 1944) Son
théorème propose une borne impliquant une constante que les mathématiciens
cherchent à préciser. |
Pour une progression arithmétique an + d, alors
il existe deux nombres positifs c et L tels que: p(a, d) < cdL Avec a et d premiers entre eux et |
|
|
Constante de Linnik L |
L < 2 pour une majorité de nombres. On conjecture que p(a, d) < d2 La première estimation de L en 1957 donnait: 10
000. En 1977, on descend à 168. En 2011, on arrive à 5. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Pour tout
entier naturel r et k, il existe un entier naturel N(r, k) tel que si l'on
colorie les entiers 1, 2, … , N en r couleurs, il existe une progression
arithmétique de même couleur et de longueur k dans cette suite de nombre. Le plus
petit N(r, k) = W(r, k) est un nombre de Van der Waerden. On ne sait pas
calculer W dans le cas général. |
Exemple N(2, 3)
W(2,3) = 9 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
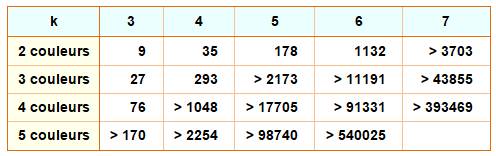
Liste des nombres de Van der
Waerden connus |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
|
Voir |
|
|
|
DicoNombre |
||
|
|
||
|
Cette page |
||