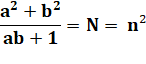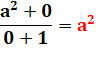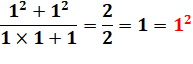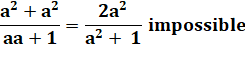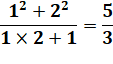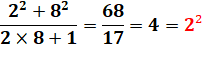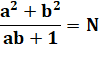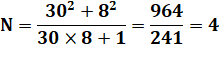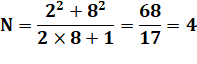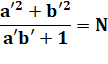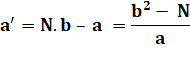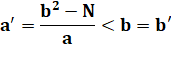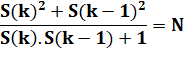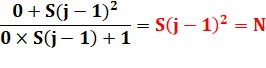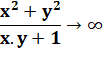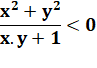|
|||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Fraction = entier au carré Si (a² + b²) / (a.b + 1) = N Alors N = n² Si cette fraction est un
entier, cet entier est un nombre au carré. |
|
|
||
|
Problème Les
nombres a et b étant des entiers positifs, montrer que si cette fraction est
un entier, alors c'est le carré d'un nombre entier. Anglais: let a and b be positive integers such that
(ab + 1) divides (a² + b²), show that (a² + b²) / (ab + 1) is the square of
an integer. |
|
|
|
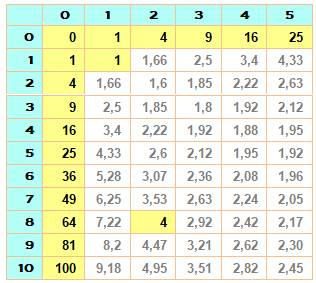
Exemple numériques avec a ou
b = 0 |
|
|
|
avec a =
b = 1 |
|
|
|
avec a =
b |
|
|
|
avec a et
b non nuls
|
En grande majorité le
résultat est une fraction; mais lorsque la fraction est réduite à un nombre,
on trouve bien un carré. Toujours? |
|
|
|
||||
|
Démonstration Elle consiste à trouver une méthode engendrant de
nouvelles solutions décroissantes dont l'une passe obligatoirement par zéro.
On montre alors que si elle ne passait pas par zéro, il y aurait une contradiction.
|
||||
|
Ce qu'il faut démontrer Soit N,
le nombre auquel se réduit la fraction. Il faut démontrer que N est un carré. |
a²
+ b² = Nab + N a²
– Nab + b² – N = 0 |
|||
|
Recherche de nouvelles valeurs C'est une
équation du second degré en x dont une des racines est a. |
x² – N.b
x + (b² – N) = 0 |
|||
|
La somme
des racines est égale à l'opposé du coefficient de x, soit N.b On note
également que leur produit est égal au terme fixe. |
x1 + x2 = N.b x1
= a x2
= N.b – a x1.x2 = b² – N |
|||
|
Exemple |
Couple de départ a = 30, b = 8
|
Calcul nouvelle valeur x2 = 4x8 – 30 = 2 Nouveau couple a' = 2, b = 8,
|
||
|
Nouvelle solution: a' et b' |
a' = N.b – a b' = b
|
|
En
reprenant les expressions de la somme et du produit en divisant par a. |
|
|
On cherche la relation d'inégalité
entre a' et b'. On sait
que a = b = 1 est résolu. On est dans
le cas où a |
b
(b – a) < 0 < N b²
– ab < N b²
– N < ab
a' < b' |
|
Relation de récurrence En répétant
ce procédé, on obtient une séquence S(k) strictement décroissante avec: S(0) = a S(1) = b avec b < a S(2) = a' = N.b – a avec a' < b' = b … S(k) = N.
S(k-1) – S(k-2) |
Récurrence qui satisfait:
|
|
La solution nulle donne un carré Est-ce
cette séquence passe par S(j) = 0 pour un entier j ? Si oui,
alors N est un carré => |
|
|
|
Mise en évidence d'une
contradiction N est le nombre
résultant de la fraction initiale réduite; N est un entier positif. Supposons
que S(j) ne passe pas par 0. Or la
séquence décroit. Alors, un
des couples de solution est tel que les deux valeurs sont de part et d'autre
de 0. Et, x =
S(n) et y = S(n+1) sont de signes opposés. |
Deux cas: Si x.y = – 1
Si x.y < – 1
Or, c'est contradictoire avec N> 0 |
|
|
Conclusion |
S(j) passe bien par une valeur nulle, et alors, N est un carré égal à S(j –
1)² |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Puissanc/Carres/FracCarr.htm
|
![]()