Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 24/04/2022 M'écrire Brèves de Maths

INDEX Théorie des nombres Types de nombres	Arithmétique – Modulo
	Introduction	Théorie	Propriétés	Formulaire
	Applications	Calculs	Carrés	Cubes
	Jeux	Sun Zi	Mod 9, 10, 11	Carrés et Cubes
	Parité	7 ^ 7 ^ 7	Log Modulaire	11^10 = 32 mod 71

CONGRUENCES Divisibilité des carrés Parmi les propriétés des carrés: ils sont des multiples de 5 ou des multiples de 5 à un près. Ils se terminent donc par 0, 1, 4, 5, 6, 9. Ex: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225 …
	Sommaire de cette page >>> Divisibilité des carrés >>> Modulo des carrés et autres puissances >>> Carrés Modulo 4 & 8	Débutants Opérations Glossaire Nombres

Divisibilité des carrés

Quels sont les restes possibles de la division d'un carré par un nombre de 2 à 13? Dans le cas de la division par 2, si le nombre est pair (2k) le carré est pair; si le nombre est impair (2k + 1), le carré est impair. Le carré conserve la parité. Dans le cas de la division par 3, le reste du cube est nul si le nombre est divisible par 3, sion il est égal à1. On dit que: a^2 = {0 ou 1} mod 3. Dans le cas de la division par 4, les restes sont aussi 0 ou 1. 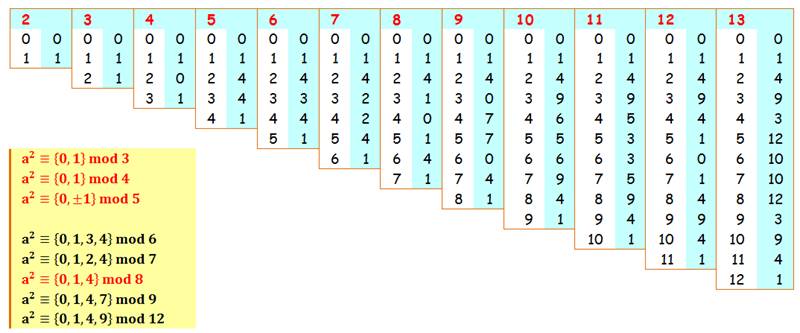Le reste de la division par m d'un nombre au carré est appelé son résidu quadratique modulo m. Tableau des résidus quadratiques: colonne bleue = reste de la division par n (rouge) du carré pour un nombre donnant le reste indiqué à gauche. La division par 5 des carrés est à noter: les restes sont nuls ou plus ou moins 1. Autrement dit: Un carré est un multiple de 5 ou un multiple de 5 plus ou moins 1.

Voir Tableau semblable pour les cubes / Machine de Carissan/ Résidus quadratiques

Somme de deux carrés

La somme de deux carrés est divisible par 4 si les deux nombres sont pairs.

Chaque carré est alors le produit (2k · 2h = 4k·h) et chacun est divisible par 4. Autre raison, un carré mod 4 = 0 pour un nombre pair et 1 pour un impair. Seule la somme de deux pairs produira une somme 0 mod 4.

La somme de deux premiers (p et q) autres que 2 n'est jamais divisible par 4. Il n'existe pas de solution a: p² + q² = 4r ou 4r² ou 8r² …

Modulo des carrés et autres puissances
Si a k mod m, alors a^b k^b mod m Exemple: si a = 5 et m = 3 alors k = 2 a^k2^ka^k mod 3 5 2 2 5^2 = 25 2^2 = 4 1 5^3 = 125 2^3 = 8 2 5^4 = 625 2^4 = 16 1 Par exemple, 5^4 et 2^4 divisés par 3 ont le même reste: 1. En effet: 625 = 208 x 3 + 1.

Table pour mod 3

a	a mod 3	a^2 mod 3	a^3 mod 3	a^4 mod 3	a^5 mod 3
1	1	1	1	1	1
2	2	1	2	1	2
3	0	0	0	0	0
4	1	1	1	1	1
5	2	1	2	1	2
6	0	0	0	0	0
7	1	1	1	1	1
8	2	1	2	1	2
9	0	0	0	0	0
10	1	1	1	1	1

En jaune les nombres a pour lesquels le résidu est le même quelle que soit la puissance: il s'agit des nombres divisibles par 3, ce qui naturel et de ces nombres plus un dont le résidu vaut 1 et reste à 1 si on l'élève à une puissance, bien évidemment.

Table pour mod 5

a	a mod 3	a^2 mod 3	a^3 mod 3	a^4 mod 3	a^5 mod 3
1	1	1	1	1	1
2	2	4	3	1	2
3	3	4	2	1	3
4	4	1	4	1	4
5	0	0	0	0	0
6	1	1	1	1	1
7	2	4	3	1	2
8	3	4	2	1	3
9	4	1	4	1	4
10	0	0	0	0	0
11	1	1	1	1	1
12	2	4	3	1	2
13	3	4	2	1	3
14	4	1	4	1	4
15	0	0	0	0	0

CARRÉS MODULO 4 & 8

En application des notions de congruences, observons les modulos 4 et 8 des carrés

Surprise ! ! !

En synthétisant

n	n² (mod 4)	n² (mod 8)
Impair	1	1
Pair	0	0 ou 4

Et démontrons...

Observations

n	n²	n² (mod 4)	n² (mod 8)
1	1	1	1
2	4	0	4
3	9	1	1
4	16	0	0
5	25	1	1
6	36	0	4
7	49	1	1
8	64	0	0
9	81	1	1
10	100	0	4
11	121	1	1
12	144	0	0
13	169	1	1
14	196	0	4
15	225	1	1

Carré (mod 4) Tout carré est congru modulo 4 à : 1 s'il est impair, 0 s'il est pair.

Démonstration Cas où n est impair => n = 2k + 1 (2k + 1)² = 4k² + 4k + 1 Il reste 1 dans la division par 4. Cas où n est pair => n = 2k (2k)² = 4 k² Divisible par 4.

Carré (mod 8) Tout carré est congru modulo 8 à : 1 s'il est impair, 0 ou 4 s'il est pair; 0 si n divisible par 4 4 sinon.

Démonstration Cas où n est impair => n = 2k + 1 (2k + 1)² = 4k² + 4k + 1 = 4 k (k + 1) + 1. k et k + 1 sont deux nombres consécutifs, l'un deux est pair. Leur produit k (k + 1) est divisible par 2, et 4 k (k + 1) est divisible par 8. Donc pour 4 k (k + 1) + 1, il reste 1 dans la division par 4. Cas où n est pair => n = 2k (2k)² = 4 k² Divisible par 4. Donc par 8 avec reste 0 ou 4. Cas où n est divisible par 4 => n = 4k (4k)² = 16 k² Divisible par 16 et a fortiori par 8.

Suite Retour	Congruences – Propriétés Approche
Voir	Divisibilité des cubes Divisibilité par 504 – Application Carrés Divisibilité Clé de divisibilité, une application de la théorie du modulo La division Exemple d'application du modulo en Codage RSA
Aussi	Calcul mental Géométrie Nombres Cycliques Nombres de Carmichaël Nombres Premiers Nombres Rationnels	Preuve par 9 – Glossaire Pseudo Premiers Pseudo Premiers Absolus Théorie des nombres Variations sur les carrés
Diconombre	Nombre 105
Cette page	http://villemin.gerard.free.fr/ThNbDemo/Mod4et8.htm