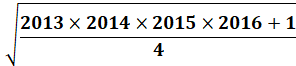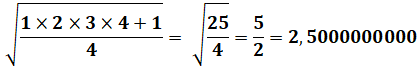|
|||||||||||||||||||||||||||||||||||
![]()
|
CALCUL d'une RACINE CARRÉE Deux
types de méthodes: Par
CALCUL (objet
de cette page) ou
Par
APPROXIMATIONS successives
|
Hep! Je conn
Ci-dessous, une approche pas à pas qui
permet d'en comprendre le mécanisme et mieux retenir la méthode.
|
Quelle
est la dixième décimale de:
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Combien de chiffres pour la racine? 1
chiffre Nombre
de 0 à 100. 2
chiffres Nombre
de 100 à 10 000. Etc. On retient que pour un chiffre de racine,
on compte deux chiffres dans le nombre. Lors des c |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
||
|
-
Prenons
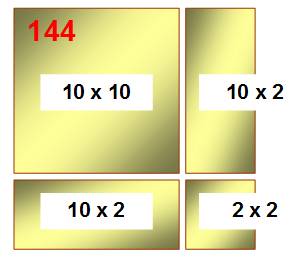
12² = 144 Connaissant
144, retrouvez la racine. -
En
décomposant dizaine et unité: 12 = 10 +
2 -
Calcul du carré (voir figure): (10 + 2)²
= 100 + 2 x 20 + 4 |
|
|
|
-
Il nous
faut imaginer le processus
inverse pour calculer la racine de 144. -
Pour
atteindre la centaine du nombre 144, il faut une racine supérieure à 10 (10 x
10 = 100), mais inférieure à 20 (20 x 20 = 400): -
Le chiffre
des dizaines de la racine est donc 1. -
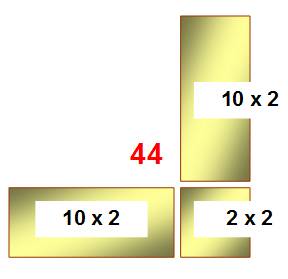
Nous
retirons le carré de 10 x 10 de la figure. -
Reste 44. |
|
|
|
-
Que savons
–nous, à ce point ? -
La racine
est égale à 1u, avec u le chiffre des unités. -
De sorte
que (voir les deux rectangles): -
Il faut
laisser une place pour le petit carré en u². -
Il suffit
de diviser 44 par 20 pour trouver u = 2,2. -
En en ne
conservant que la valeur entière u = 2. -
FIN. |
2 x (10 . u ) < 44 u < 44 / 20 = 2, 2 Retenons u = 2 Retirons les deux rectangles Reste 44 – 40 = 4 Cette valeur est bien le carré du chiffre
des unités 4 = 2 x 2 Notez l'usage
du point ou du signe x pour signifier multiplication |
|
|
Posons l'opér |
|||||||||||||||||||||||||||||||||||||||||
|
-
Nombre 144 en rouge: -
La valeur de la racine se place en
haut au fur et à mesure qu'elle est connue. -
Les calculs intermédiaires sont
placés en dessous. |
|
||||||||||||||||||||||||||||||||||||||||
|
Étape 1 -
On considère le chiffre des
centaines: 1. -
Quel est le nombre qui au carré
donne 1: -
Seul 1 est valable; 2 est trop
grand, -
On pose 1 en haut. -
Soit une dizaine pour la racine et
une centaine pour son carré. |
|
||||||||||||||||||||||||||||||||||||||||
|
Étape 2 -
On considère maintenant le nombre
complet. -
On retire la centaine déjà trouvée. -
Il reste 44. |
|
||||||||||||||||||||||||||||||||||||||||
|
Étape 3 -
On prend le chiffre de la racine 1. -
C'est une dizaine 10. -
Deux fois cette valeur. -
Combien de fois au maximum dans 44. -
Deux semble convenir. |
|
||||||||||||||||||||||||||||||||||||||||
|
Étape 4 -
On retient 2 pour la racine, et on
place ce chiffre en haut. -
Tout en retranchant la contribution
de 2, soit 2 x 10 x 2 = 40. -
Qui donne 4; qui est le carré de
l'unité. -
L'extraction de la racine est terminée:
FIN. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calculez Étape 1: chiffre des dizaines -
Blocs de 2
chiffres en partant de la droite. -
Premier
bloc à gauche. -
Quelle est
sa racine carrée: -
7 x 7 = 49 -
8 x 8 = 64
trop grand -
on retient
7 -
et on
retire les 49; reste 4 -
On abaisse
le bloc suivant. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Étape 2: chiffre des unités -
On se souvient
de la figure montrant la décomposition où intervient une histoire de deux
rectangles identiques. -
En bref,
il faut trouver un chiffre des unités tel que 2 x 70 x u inférieur à 429. -
Ou encore
u < 429 / 140. -
soit la
valeur de u = 3. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Étape 3: bouclage final -
On pose 3
comme chiffre des unités de la racine. -
On
retranche la contribution de ce 3 soit 420. -
Reste 9 qui
est bien le carré de l'unité. -
FIN. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Nous venons de voir le mécanisme de l'extraction de la
racine carrée expliquée pas à pas. Voici maintenant la méthode telle que vous pouvez la
pratiquer avec un peu d'habitude. |
|
|
||||||||||||||||||||||||||||||
|
Calculez -
Blocs de 2 chiffres en partant de la
droite. -
Premier bloc à gauche: 34. -
Sa racine: -
On retient 5 et on retire sa
contribution 25. -
Valeur de u < 981 / (2 x 50) =
9,8 -
On retient 9 et on retire sa
contribution 2 x 50 x 9 = 900 -
Reste 81 qui est bien le carré du
chiffre des unités. -
FIN. |
|
|||||||||||||||||||||||||||||
|
Calculez -
Blocs de 2 chiffres en partant de la
droite -
Premier bloc à gauche: 24. -
Sa racine: -
On retient 4 et on retire sa
contribution 16 -
Valeur de u < 801 / (2 x 40) =
10,01 -
La valeur entière
inférieure à 10,01 est 10. Cependant une petite vérification: 50 x 50 = 2500
qui est > 2401. Alors la racine est < 50. Ce serait donc 49? Le 1 des
unités le laisse également supposer 9 x 9 = 81). -
On retient donc 9 et on retire sa
contribution 2 x 40 x 9 = 720 -
Reste 81 qui est bien le carré du
chiffre des unités. -
FIN. |
Exemple d'un cas un peu délicat, soulevé par un internaute (Merci à Adrien L.)
|
|||||||||||||||||||||||||||||
|
Quelle
est la dixième décimale de:
Bien
sûr la calculette va donner
le résultat: 2 029 104, 5000000000. Il
existe une solution sans faire le calcul. Une
identité remarquable avec des nombres successifs: n (n + 1) (n + 2) (n + 3) + 1 = (n² + 3x + 1)² De
sorte que le terme sous le radical est un carré impair La
racine est un nombre entier divisé par 2. Sa
première décimale est 5 et les suivantes sont 0. En
outre, nous avons montré que le résultat est toujours 0 quels que soient les
quatre nombres successifs choisis. Par exemple:
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |