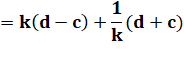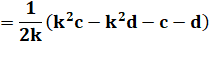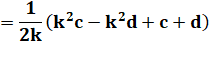|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DIFFÉRENCE des carrés N = b² – a² = d² – c² = … M = a²+ d² = b² + c² = … Quelle sont les
solutions de ces équations
diophantiennes? Différence de carrés = différence de carrés ou ce qui revient
au même: Cherchez les sommes de carrés qui
sont égales. Réponse: une infinité de solutions! Exemple:
Cerise
sur le gâteau! Concaténation
des nombres et leur retournement:
84² –
71² = 48² – 17² = 7 056 – 5 041 = 2 304 – 289 = 2
015 1311²
– 701² = 1113² – 107² = 1 718
721 – 491 401 = 1 238 769 – 11 449 = 1 227 320 1311²
– 804² = 1113² – 408² = 1 718 721 – 646 416 = 1 238 769 – 166 464
= 1 072 305 |
|
|
|||
|
Le problème posé: trouver
quatre nombres entiers tels que la différence des carrés deux à deux soient
égales. |
b² – a² |
= d² – c² |
|
|
Ce qui équivaut à une
égalité entre somme de carrés. |
a² + d² |
= b² + c² |
|
|
En factorisant avec une identité remarquable: |
N = (b –
a) (b + a) |
= (d – c) (d + c) |
|
|
Cette présentation permet de
conclure que N et un nombre qui doit être factorisable de deux manières. |
N = P x Q |
= R x S |
|
|
Exemple |
15 = 1 x 15 |
= 3 x 5 |
|
|
Il s'agit de convertir ces
facteurs en somme et différence de couples de nombres. |
15 = 7 + 8 5 = 4 + 1 |
et 8 – 7 = 1 et 4 – 1 = 3 |
|
|
En remontant le calcul: |
15 = (8 – 7) (8 + 7) |
= (4 – 1) (4 + 1) |
|
|
|
N = 8² – 7² 15 = 64 – 49 |
= 4² – 1² = 16 – 1 |
|
|
Exprimé sous forme de somme: |
M = 7² + 4² 49 + 16 |
= 8² + 1² = 64 + 1 = 65 |
|
|
|
|
|
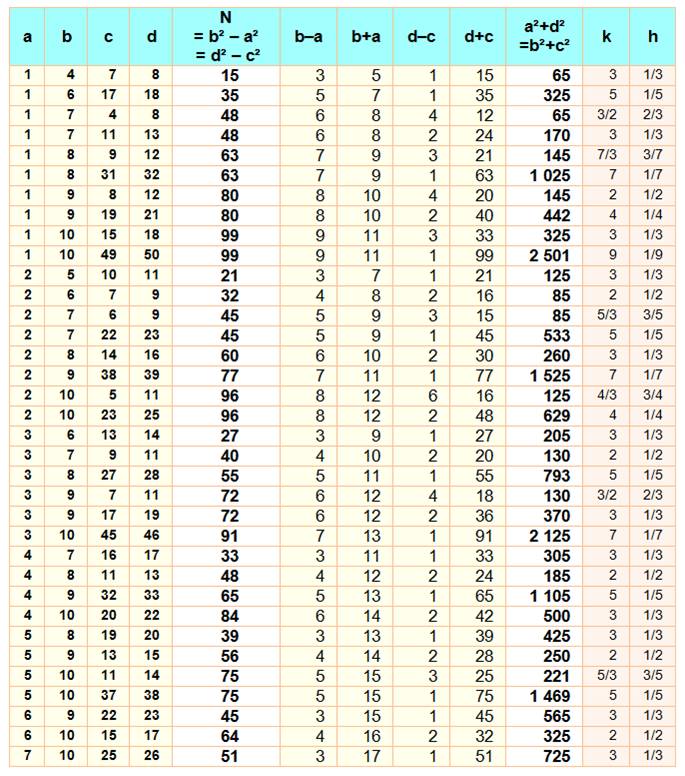
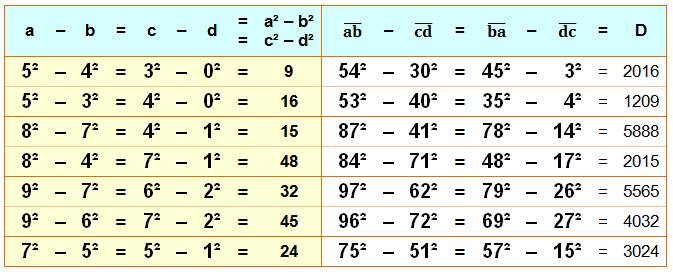
Les premières valeurs de a
et b jusqu'à 10 puis c et d jusqu'à 100. Avec a, b, c et d différents. On reconnait la première
ligne avec N = 4² – 1² = 8² – 7². Les quatre colonnes
suivantes montrent les quatre facteurs: N
= 3 x 5 = 1 x 15. La suivante indique
l'égalité des sommes de carrés: 49 +
16 = 64 + 1 = 65. Les deux dernières colonnes
seront expliquées ci-dessous.
48 = 1² – 7² =
8² – 4² = 13² – 11² 120 =
11² – 1² = 13² – 7² = 17² – 13² = 31² – 29²
288
= 17² – 1² = 18² – 6² = 22² – 14² = 27² – 21² = 38² – 34² = 73² – 71² 960
= 31² – 1² = 32² – 8² = 34² – 14² = 38² – 22² = 46² – 34² = 53² – 43² 1 680
= 41² – 1² = 43² – 13² = 44² – 16² = 47² – 23² = 52² – 32² = 67² – 53² |
|
|
|
|||
|
En reprenant la
factorisation: |
N = (b – a) ( b + a) |
= (d – c) (d + c) |
|
|
Les facteurs doivent se
retrouver de part et d'autre de l'égalité. Alors supposons: |
b – a b + a |
=
k (d – c) = 1/k (d +
c) |
|
|
Somme de ces deux
expressions: |
2b |
|
|
|
|
b |
|
|
|
|
a |
|
|
|
Impasse! |
La valeur de k = (d + c) /
(b + a) et celle de h = (d – c) / (b – a) sont indiquées dans les deux colonnes
de droite du tableau. |
||
|
|
|||
|
En reprenant la somme des
carrés |
M = a² + d² |
= b² + c² |
|
|
Nous reconnaissons là un
problème connu! Quels sont les nombres qui
peuvent se présenter comme plusieurs fois la somme de deux carrés. La première condition: que
le nombre M soit un nombre somme de deux carrés. |
|
||
|
Exemple m = 65 (première ligne du tableau) |
65 |
= 5 x 13 = (1x4 + 1) x (2x4 + 1) |
|
|
C'est la bonne piste! |
Toutes les égalités de somme
de carrés peuvent se transformer en égalité de différence de carrés. |
||
|
|
||
|
Je connais M, somme de deux
carrés deux fois, il est facile d'en déduire une différence de carrés. Il suffit de faire basculer
un carré de chaque côté vers l'autre côté de l'égalité. |
M = 7²
+ 4² = 8² + 1²
= 65 N = 4² – 1² = 8² – 7² = 15 |
|
|
Nouvel exemple avec 325,
avec lequel nous forgeons trois fois l'égalité de différence de carrés. |
M = 1² + 18² = 6² + 17² = 10² + 15² N = 18² – 17² = 6² – 1² = 35 N' = 18² – 15² = 10² – 1² = 99 N" = 17² – 15² = 10² – 6² = 64 |
|
Voir Somme
de deux carrés deux fois – Autres exemples
|
Propriété
remarquable de a² – b² = c² – d² Création
de ce motif en cascade |
|
|
|
|
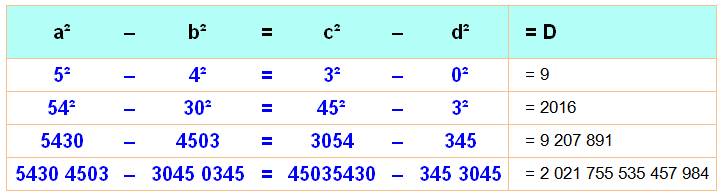
8² – 4² = 7² – 1² = 64 – 16 = 49 – 1 = 48 84² – 71² = 48² – 17² = 7 056 –
5 041 = 2 304 – 289 = 2 015 |
|
|
|
Notons a,
b, c et d, les quatre nombres a un chiffre. Leur
concaténation donne: Leur
retournement |
|
|
|
D = ((10a + b)² – (10c + d)²) – ((10b + a)² – (10d + c)²) |
|
|
|
D = 100a² + 20ab + b² – 100c² –20cd – d² – 100b² – 20ab
– a² + 100d² + 20cd + c² D = 99a² –
99b² – 99c² + 99d² D = 99 (a² – b²
– c² + d²) |
|
|
|
a² – b² – c² + d² = 0 a² –
b² = c² – d² |
|
|
Soit un nombre différence de deux carrés deux fois. La concaténation
des carrés et leur retournés forment également un nombre différence de deux
carrés deux fois. |
||
Les sept seuls cas pour les chiffres de 0 à 9
On note: trois cas avec permutations et un cas
unique comportant deux 5.
Le tableau peut être prolongé comme nous allons le voir tout de suite.
Merci à André M. pour
ces résultats
|
Extraordinaire: la propriété
est valable pour les nouvelles différences de carrés. Attention de retourner les nombres
et non les chiffres.
|
|
Justification
avec des nombres de k chiffres Leur
concaténation donne: Leur
retournement Le calcul
conduit à: Nous
retrouvons les mêmes conditions: pour que D = 0. Il suffit que: a² – b² – c² + d² = 0. |
|
Dans le
cas d'un triplet de Pythagore, nos propriétés
subsistent, à condition de mettre un des nombres à 0. Exemple de cascade (quatre étapes) avec le
triplet 5² = 4² – 3²
|
Voir Le
triplet de Pythagore le plus célèbre
|
Il
existe une infinité de cas tels qu'un nombre soit égal à la différence de deux
carrés au moins deux fois. Par
concaténation et retournement, il est possible de créer une cascade sans fin
de tels nombres à partir d'une configuration initiale. Les
triplets de Pythagore n'échappent pas à cette propriété. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/P100a500/Difmult.htm
|
![]()