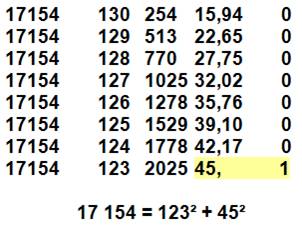|
|||||||||||||||||||||||||||||||
![]()
|
SOMME de deux CARRÉS Introduction Tout nombre est somme de quatre carrés, au plus Quels sont ceux pour lesquels trois suffisent? Et deux seulement? Un carré somme de deux carrés est un triplet
de Pythagore: C² = A² + B² Ici, la question est: quel sont les nombres qui sont somme de deux
carrés (ou plus): N = A² + B² |
Anglais: sum of two square
problem or Girand's problem (1627)
|
Théorème
des deux carrés de Fermat – Nombres premiers Tout
nombre PREMIER est la somme de deux carrés de façon unique si et seulement si
il est de la forme 4n + 1. Théorème
des deux carrés – Nombres quelconques Un
entier est somme de deux carrés si et seulement si chacun de ses facteurs
premiers de la forme 4k + 3 est à une puissance paire. De
plus, la décomposition est unique si aucun facteur n'est en 4k + 1, ou alors
un seul à la puissance unité. |
Voir Ces
théorèmes / Structure
des nombres premiers
|
|
||
|
Seuls certains nombres peuvent être somme
de deux carrés. Qui sont-ils ? Est-il facile de les caractériser? Oui, mais pas tout à fait immédiat. |
1 = 1² 2 = 1² + 1² 3 = 1² + 1² + 1² 4 = 2² 5 = 2² + 1² 6 = 2² + 1² + 1² 7 = 2² + 1² + 1² + 1² 8 = 2² + 2² Etc. |
|
|
|
||
|
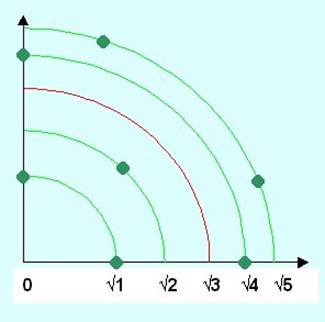
n = x² +
y² Trouver si un nombre est somme de deux
carrés, c'est chercher s'il existe un point de coordonnées entières sur le
cercle de rayon Les sommes représentées sont les
suivantes:
|
|
|
|
|
||
|
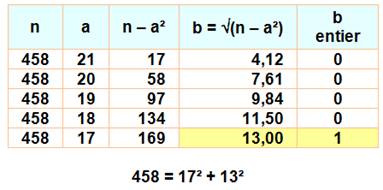
Testons si un nombre donné est somme
de deux carrés. Comment s'y prendre? Un peu à la manière du crible
d' Ératosthène. Il faut démarrer par la racine du nombre ou plus
exactement, l'entier inférieur le plus proche de la racine. Exemple: 458 => Il faut procéder par étapes en
faisant décroître ce terme a. Arrêt dès que la soustraction donne
un carré. |
|
|
|
Autres exemples de calcul
|
|
|
|
|
||
|
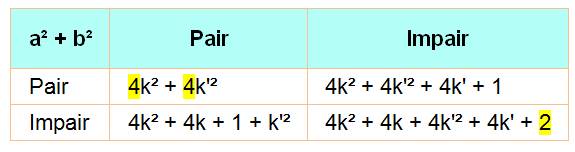
On sait qu'un nombre n'est pas
toujours somme de deux carrés. On sait trouver les termes de la
somme si elle existe. Que peut-on dire de plus ? Il faut passer par une phase
d'observation avant de trouver des propriétés éventuelles. On introduit la fonction h(n) qui vaut
|
Suite
Voir
|
|
Divisibilité de la somme de deux carrés
|
La somme de deux carrés de nombres pairs est divisible par 4. Celle de deux nombres impairs l'est par
2.
|
|
|
||
|
Dans cette somme de deux carrés, l'un des termes est pair. |
a² + b² =
c² a ou b est pair |
|
|
Supposons que
l'égalité soit vraie avec a et b impairs. |
a² + b² = (2k +
1)² + (2h + 1)² = 4k² + 4j + 1 +
4h² + 4h + 1 = 4 K + 2 avec K
un entier positif |
|
|
Comparé à c: |
c² = 4K + 2 |
|
|
Or un carré divisé
par 4 ne donne jamais 2 comme reste. |
c = 2a c = 2a + 1 |
|
|
Contradiction. |
Notre hypothèse
est fausse. |
|
|
|
||
|
La différence des carrés de deux nombres premiers n'est jamais un
carré de premier. |
a² – b² |
|
|
Supposons que l'égalité
soit vraie. En remarquant
que le carré est positif |
a² – b² =
c² |
|
|
a² – b² = (a –
b) (a + b) |
||
|
Le premier
membre est positif |
a + b > 1
évident a – b |
|
|
1) Supposons que a – b = 1 Or a et b sont
premiers. |
Seule
possibilité: a = 3 et b = 2 |
|
|
L'égalité
devient: |
3² – 2² = 9 – 4
= 5 qui n'est pas un carré. |
|
|
2) Supposons que a – b > 1 Or c est un nombre
premier et ses facteurs sont 1 et c. |
a² – b² = (a –
b) (a + b) = c² |
|
|
Cependant: |
a + b > 1 a – b > 1 |
|
|
Aucun facteur ne
peut égaler 1. |
La contradiction
infirme notre hypothèse. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/SomCaPre.htm |
![]()