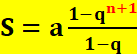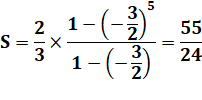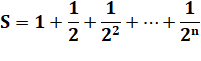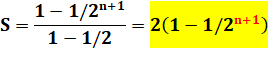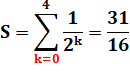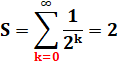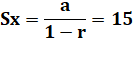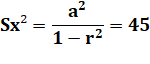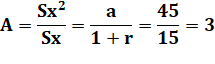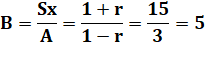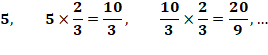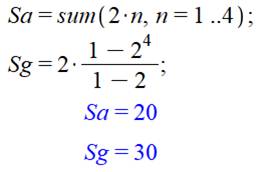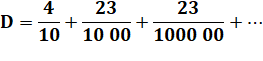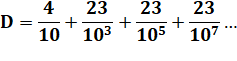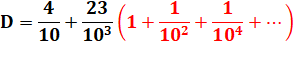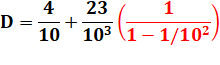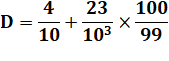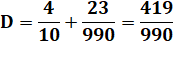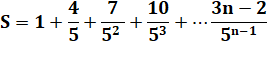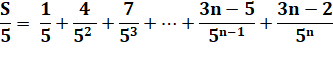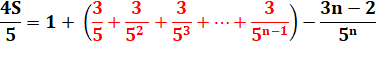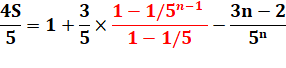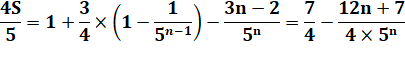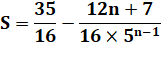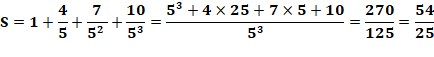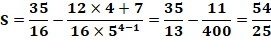|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
SUITE
GÉOMÉTRIQUE Exemples
de calculs Un florilège
d'exemples de calculs avec les suites et séries
géométriques. |
Anglais: Geometric
progression, common ratio (= raison)
Retour: Suite géométrique
Voir Moyenne géométrique / / Suite et Série
Rappel
de la formule fondamentale
|
S: somme de la série; a: son premier terme; q: la raison (le coefficient
multiplicateur); et n: la dernière puissance utilisée
(de 0 à n) pour n + 1 termes dans la
série. |
Exemple 5 + 15 + 45 + 135 = 200 Paramètres a = 5, q = 3, n = 3 (mais, avec quatre termes) Calcul
|
|
|
||
|
Une
PG de 6 termes 5, a, b, c, d, 160 Raison
et termes intermédiaires? |
Équation 160
= 5 q5 q
= (160/5)1/5 = 321/5 = 2 Solution 5,
10, 20, 40, 80, 160 |
|
|
Une
PG de 5 termes 2/3, -1, 3/2 Raison
somme? |
Raison q
= (–1) / (1/3 = –3/2 Somme
|
|
Calcul de S

|
Somme
des inverses des carrés de 2 Pour
k tendant vers l'infini la limite de la somme est égale à 2. |
Exemple avec n = 4 S = 1 + 1/2 + 1/4 + 1/8 + 1/16 = 31 / 16 = 1,9375 S = 2 (1 - 1 /
32) = 2 (31 / 32) = 31 / 16 Notation
|
Voir PG -
Exemples
|
Trois
nombres en PG dont la somme vaut 19 et le produit 216. Trouvez
ces nombres. Indice: une astuce de notation simplifie
grandement le calcul. |
On
note la PG à partir du terme central: a/q,
a et a.q Alors,
le produit devient: P
= a3 = 216 a
= 6 Et,
la somme 6/q
+ 6 + 6q = 19 6
+ 6q + 6q² = 19q 6q²
– 13q + 6 = 0 q1
= 3/2 et q2 = 2/3 Les
nombres 4,
6 et 9 |
|
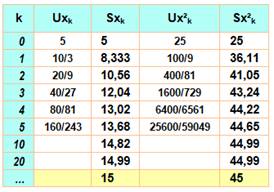
La
somme de cette PG infinie est 15 et la somme des carrés est égale à 45. Quelle
est cette série? Les deux PG Somme des nombres
avec a au départ et une raison r. Somme des carrés avec a² au départ et
raison r². Chaque terme de cette série et le carré de ceux de la précédente. Les termes de la série
|
Sommes infinies
Division de l'une par l'autre
Valeur de la raison r 1 + r = 5 – 5r => r =
2/3 Série a = 15 – 15r => a = 5
|
|
|
||
|
Ne
pas confondre les deux types de séries; arithmétique et géométrique. Notamment
lors de l'emploi de logiciels. Ne
pas utiliser l'instruction somme pour une progression géométrique. |
Exemple Sa
= 2 + 4 + 6 + 8 + … PA (r = 2) Sg
= 2 + 4 + 8 + 16 + … PG (q = 2) Formules de calcul
|
|
|
|
||
|
D
= 0,4232323… |
||
|
Écriture
fractionnaire |
|
|
|
Série
géométrique infinie de raison q = 1/10² |
|
|
|
Notez que: |
419 = 423 – 4 99 et 23: même
quantité de chiffres 0 et 4: idem |
|
|
Somme mixte |
|
|
|
Calculs |
|
|
|
PG (g = 1/5) |
|
|
|
Exemple |
|
|
|
|
|||
|
PG (a, b, c, d) |
(d – a)² = (d – b)² + (b – c)² + (c – a)² Théorème Il est toujours
possible de créer une carré somme de trois carrés avec quatre nombres en
progression géométrique. Démonstration Avec b = a.g, c = a.g2 et
d = a.g3 (d
– b)² + (b – c)² + (c – a)² =
a2g6 – 2a2g4
+ a2g2 + a2g4 – 2a2g3
+ a2g2 + a2g4 – 2a2g2 + a2 =
a2g6 – 2a2g3 + a2 =
(a.g3 – a)² = (d – a)2 |
||
|
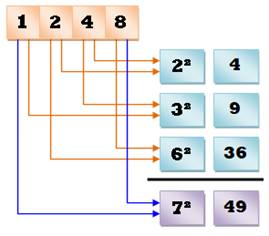
Exemple |
PG
(1, 2, 4, 8) (8
– 1)² = (4 – 2)² + (4 – 1)² + (8 – 2)² = 2² + 3² + 6² = (8 – 1)² = 7² 2² + 3² + 6² = 7² |
|
|
|
Table |
PG 1, 2, 4, 8 1, 3, 9, 27 1, 4, 16, 64 1, 5, 25, 125 1, 6, 36, 216 1, 7, 49, 343 1, 8, 64, 512 1, 9, 81, 729 1, 10, 100, 1000 |
Termes de l'égalité 2, 3, 6, 7 6, 8, 24, 26 12, 15, 60, 63 20, 24, 120, 124 30, 35, 210, 215 42, 48, 336, 342 56, 63, 504, 511 72, 80, 720, 728 90, 99, 990, 999 |
|
Voir Sommes de
carrés – Formules / Carrés
– Index
![]()
|
Retour |
|
|
|
|
|
Cette page |