|
Devinette
|
Quelle est la surface où l’on cherche le rayon pour trouver le volume ?
La bibliothèque ! |
Voir Jeux
et énigmes
|
Approche |
On
peut illustrer une multiplication en dessinant un rectangle Ici, 3 x 2 = 6 La figure s'étend sur 6 pavés L'aire de cette surface est 6 pavés |
|
|
Définition |
Aire: mesure de la surface; quelle est la grandeur de la surface, son
étendue? Aire d'un solide: somme des aires des faces du solide. Aire latérale d'un solide: somme des aires des faces latérales de certains
solides comme les prismes, les pyramides ou les cylindres |
|
|
Unités |
kilomètre carré km² x 1 000² = 1 000 000 = 106 hectomètre carré hm² x 100² = 10 000 = 104 décamètre carré dam² x 10² = 100 = 102 mètre carré m² x 1² décimètre carré dm² x 0,1² = 0,01 = 10-2 centimètre carré cm² x 0,01² = 0,0 001 = 10-4 millimètre carré mm² x 0, 001² = 0,000 001 = 10-6 |
|
|
Anglais |
Area: extent or
measure of a surface The garden is
twelve square meter in area |
![]()
![]()
|
|
||
|
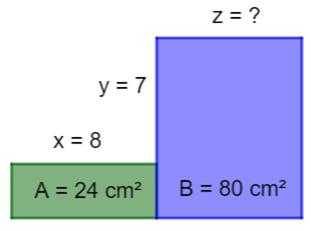
Problème Deux rectangles dont on connait l'aire et les
deux dimensions x et y indiquées. Quelle la longueur du côté z ? Solution Imaginez un troisième rectangle au dessus du
vert. Son aire est: 7 x 8 = 56 cm². L'aire du nouveau grand rectangle
(imaginaire + vert) = 24 + 56 = 80
cm². Soit l'aire du rectangle bleu. Les deux grands
rectangles sont identiques et ils ont la même longueur, les largueurs
sont égales. |
|
|
|
|
||
|
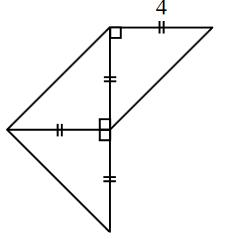
Quelle
est l'aire de cette figure? Aire du triangle en haut à droite: ½ x 4 x 4 =
8cm². Aire des deux triangles de gauche qui, assemblés,
forment un carré de 4 x 4, soit 16 cm². Aire de la figue complète: 8 + 16 = 24 cm² On aurait peu dire aussi que les trois triangles
sont égaux et que l'aire de la figure est égale à 3 x 8 = 24 cm². |
|
|
|
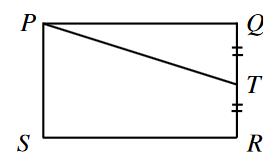
Si l'aire
de PQRS est 24 cm², quelle est l'aire de PTRS? T est le point milieu du
segment QR. Le point T est le milieu de QR. Soit T' le milieu
de PS. Le segment TT' partage le rectangle en deux parties égales. La
diagonale PT du rectangle PQTT', partage ce rectangle en deux. L'aire de PTRS vaut les 3/4 de celle du
rectangle, soit: 24 x 3/4 = 18cm² |
|
|
|
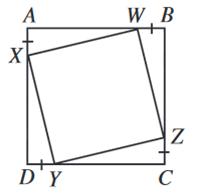
L'aire du
carré ABCD est égale à 64 cm². Les segments AW, BZ, CU et DY mesurent 2cm. Quelle
est l'aire du carré intérieur WXYZ? Le côté du carré mesure racine de 64 = 8 cm. Les quatre triangles rectangles ont des côtes à
angle droit qui mesurent 2 cm et 6 cm. L'aire totale est égale à 2 x (2 x 6)
= 24 cm². L'aire du carré intérieur vaut: 64 – 24 = 40 cm² |
|
|
|
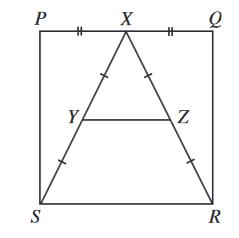
Le carré
PQRS a un côté qui mesure 8 cm. Le point X est le milieu de PQ. Les points Y
et Z sont les milieux des segments SX et RX. Quelle est l'aire du trapèze
YZRS? Constatons que YZ = PX = XQ = 4cm (Théorème de Thalès). Construisons les perpendiculaires à SR passant
par Y et Z avec Y' et Z' comme pieds. YZZ'Y' est un carré de 4 cm de côté,
dont l'aire vaut 16 cm². Les deux triangles YY'S et ZZ'R, assemblés,
forment un rectangle de 4cm par 2 cm dont l'aire vaut 8 cm² L'air du trapèze est égale à 16 + 8 = 24 cm². |
|
|
|
Aire
totale de toutes les faces d'une boite de dimensions 10 cm, 12 cm et 20 cm? C'est la
somme des aires des six faces ou le double de la somme des aires des trois
faces différentes. A = 2 x (10 x 12 + 10 x 20 + 12 x 20) = 2 x
(120 + 200 + 240) = 2 x 560 = 1 120 cm² |
|
|
|
Piscine
circulaire de 94,25 m de périmètre. Une bordure à daller de 3 m de large
autour de la piscine. Aire de la surface à daller? Rayon de la piscine: 2 x 3,14 x R = 94,25 R = 94,25 / (2 x 3,14) = 15 m Aire de la piscine: 3,14 x 15² = 706,86 Rayon avec trottoir: 15 + 3 = 18 m Aire avec trottoir: 3,14 x 18² = 1017,88 Aire à daller: 1017,87 – 706,86 = 311,02 m² |
|
|
Voir Brèves calcul
d'aires en 678
/ 690
/ 724
|
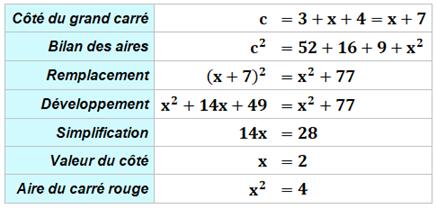
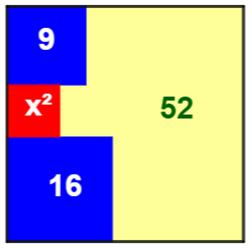
Problème Trois carrés dans un grand carré. On connait l'aire des deux carrés bleus L'aire montrée en jaune vaut 52. Quelle est l'aire du carré rouge ? Solution
|
|
|
![]()
|
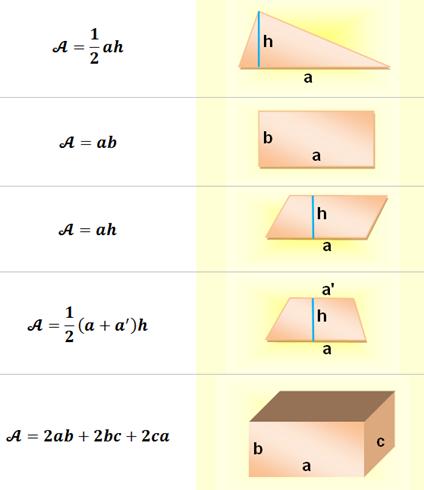
Arêtes droites |
|
|
|
Triangle |
|
|
|
Rectangle |
||
|
Parallélogramme |
||
|
Trapèze |
||
|
Pavé droit (parallélépipède rectangle) |
||
|
Arêtes courbes |
|
|
|
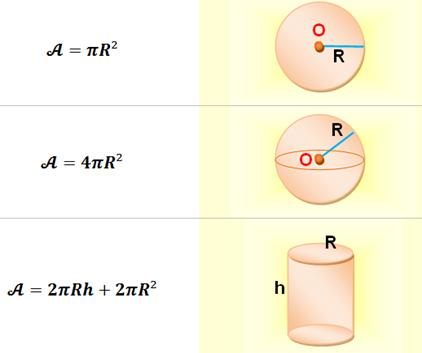
Disque (cercle) |
|
|
|
Sphère |
||
|
Cylindre |
||
Voir aussi Mon
petit formulaire / Formulaire
complet: périmètres, aires, volumes
|
Aire - Index |
Débutants
Aires
Général
|
|
Sites |
Ke!san Online
Calculator – Casio – Calcul de l’aire de très nombreuses figures. |
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosA/Aire.htm |