|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
9-REPDIGIT Nombres
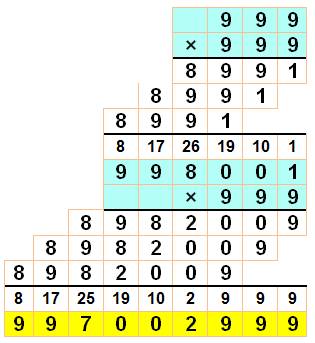
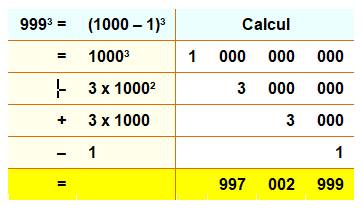
avec le chiffre 9 répété. Exemple de propriété avec le cube des 9-repdigits
Ce motif est itératif (semblable quelle que soit
la quantité de 9) >>> |
Voir Multiplication
posée
|
|
|
|
|
||
|
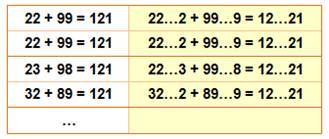
Notez ce
motif:
|
|
|
Suite en Divisibilité
par 99 …9
|
|
|
|
Résultat
Somme 3 Nombre 999 Double 1 998 998 + 1 = 999 Carré 998 001 998 + 1 = 999 Cube 997 002 999 997 + 2 + 999 = 2 x 999 P4 996 005 996 001 996 + 5 + 996 + 1 = 2 x 999 P5 995 009 990 004 999 995 + 9 + 990 + 4 + 999 = 2 x 999
|
|
Voir Nombres de Kaprekar
|
|
||||
|
Repdigit |
Double |
Carré |
Cube |
|
|
9 |
18 |
81 |
7 2 9 |
|
|
99 |
1 98 |
98 01 |
97 02 99 |
|
|
999 |
1 998 |
998 001 |
997 002 999 |
|
|
9 999 |
1 9998 |
9998 0001 |
9997 0002 9999 |
|
|
99 999 |
1 99998 |
99998 00001 |
99997 00002 99999 |
|
|
999 999 |
1 999998 |
999998 000001 |
999997 000002 999999 |
|
|
|
|
|
9 = 10 – 1 99 = 100 – 1 999 = 1000 – 1 Etc.
999
x 2 = (1000
– 1) x 2 = 1000 + 998 => 1 + 998 = 999
9992 = (1000
– 1)2 = 1 000 000 – 2 000 + 1 = 998 000 + 1
|
|
|
|
||
|
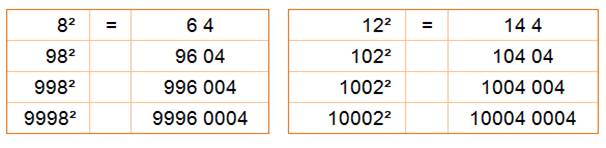
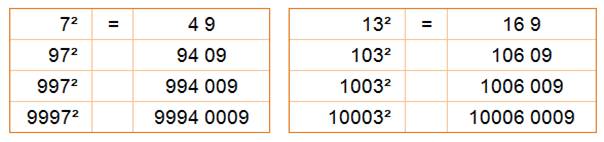
= (n – 2) n + 1
= (n + 2) n + 1 |
Voir Nombre
98 et calcul du carré |
|
|
|
||
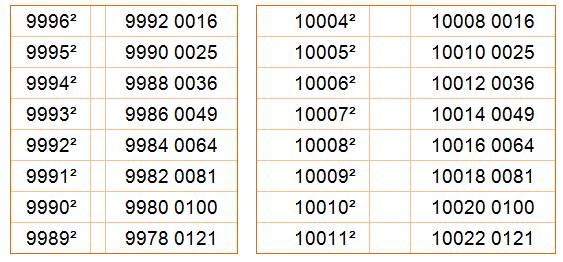
Voir 999 est magique / 999 et fractions / Passage d'un nombre carré au suivant
/ Magie
DicoNombre 9800
|
|
||
|
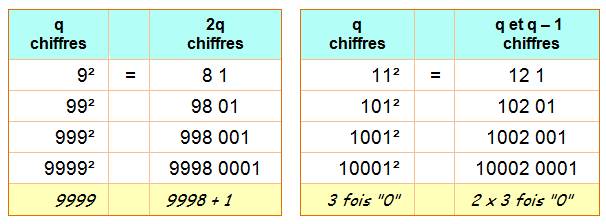
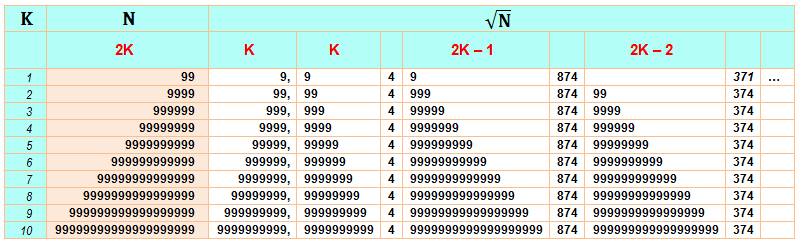
Présence
du chiffre 9 en cascade dans la racine carrée des 9-repdigits ayant 2k
chiffres. La
deuxième ligne du tableau (rouge) indique la quantité de chiffres 9 qui se
répètent |
Pour
information
|
|
|
|
||
|
Mise en
évidence à l'aide d'une identité remarquable
d'une formule en fonction de racine de 99. L'autre nombre étant un nombre en 10101 … |
|
|
|
Propriété
remarquable avec le nombre de
Lewis Carroll (tous les chiffres sauf le 8). |
|
|
Voir Racines carrées et leurs décimales
Racine
carrée des nombre en 992k avec 100 chiffres
(Notation anglaise avec le point
décimal au lieu de la virgule, le 9-repdigit concerné est indiqué en bout de
ligne)

![]()
Puissances des nombres en 999…
|
Les puissances des nombres en 999… engendrent des motifs répétitifs. Cela est dû au fait que: 999 = 1000 – 1, par exemple. Pour le
cube (exemple du tableau): (a – 1)3 = a3 – 3 a2 + 3a – 1. La présence des "0", laisse la place à certains motifs pour
s'exprimer. |
|
|
n |
n2 |
n3 |
n4 |
n5 |
|
9 |
81 |
729 |
6561 |
59049 |
|
99 |
9801 |
970299 |
96059601 |
9509900499 |
|
999 |
998001 |
997002999 |
996005996001 |
995009990004999 |
|
9999 |
99980001 |
999700029999 |
9996000599960001 |
99950009999000049999 |
|
99999 |
9999800001 |
999970000299999 |
99996000059999600001 |
9999500009999900000499999 |
|
n |
n6 |
n7 |
|
9 |
531441 |
4782969 |
|
99 |
941480149401 |
93206534790699 |
|
999 |
994014980014994001 |
993020965034979006999 |
|
9999 |
999400149980001499940001 |
9993002099650034997900069999 |
|
99999 |
999940001499980000149999400001 |
99993000209996500034999790000699999 |
|
n |
n8 |
n9 |
|
9 |
43046721 |
387420489 |
|
99 |
9227446944279201 |
913517247483640899 |
|
999 |
992027944069944027992001 |
991035916125874083964008999 |
|
9999 |
99920027994400699944002799920001 |
999100359916012598740083996400089999 |
|
99999 |
9999200027999440006999944000279999200001 |
999910003599916001259987400083999640000899999 |
Voir Records de 9 dans les
puissances de n
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Cette page |
![]()