|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CALCUL
des CARRÉS
|
|
|
||
|
Nous utiliserons la méthode générale. Formule
générale (10b + a)² = 100b² + 20ab + a² Notez Quelques formes
particulières qui méritent de les retenir par cœur. |
Exemples 33² =
900 + 180 + 9 = 1 089 37² =
900 + 420 + 49 = 1 369 38² =
900 + 480 + 64 = 1 444 73² = 4 900
+ 420 + 9 = 5 329 77² = 4 900
+ 980 + 49 = 5 929 78² = 4 900
+ 1 120 + 64 = 6 084 83² = 6 400
+ 480 + 9 = 6 889 87² = 6 400
+ 1 120 + 49 = 7 569 88² = 6 400
+ 1 280 + 64 = 7 744 |
|
|
Carrés
des nombre de 0 à 99 complet |
|
||||||||||
|
D
/ U |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0. |
0 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
|
|
1. |
100 |
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
|
|
2. |
400 |
441 |
484 |
529 |
576 |
625 |
676 |
729 |
784 |
841 |
|
|
3. |
900 |
961 |
1 024 |
1 089 |
1 156 |
1 225 |
1 296 |
1 369 |
1 444 |
1 521 |
|
|
4. |
1 600 |
1 681 |
1 764 |
1 849 |
1 936 |
2 025 |
2 116 |
2 209 |
2 304 |
2 401 |
|
|
5. |
2 500 |
2 601 |
2 704 |
2 809 |
2 916 |
3 025 |
3 136 |
3 249 |
3 364 |
3 481 |
|
|
6. |
3 600 |
3 721 |
3 844 |
3 969 |
4 096 |
4 225 |
4 356 |
4 489 |
4 624 |
4 761 |
|
|
7. |
4 900 |
5 041 |
5 184 |
5 329 |
5 476 |
5 625 |
5 776 |
5 929 |
6 084 |
6 241 |
|
|
8. |
6 400 |
6 561 |
6 724 |
6 889 |
7 056 |
7 225 |
7 396 |
7 569 |
7 744 |
7 921 |
|
|
9. |
8 100 |
8 281 |
8 464 |
8 649 |
8 836 |
9 025 |
9 216 |
9 409 |
9 604 |
9 801 |
|
Remplissage
100 / 100
|
|
||
|
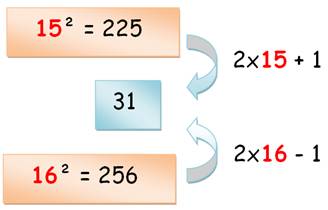
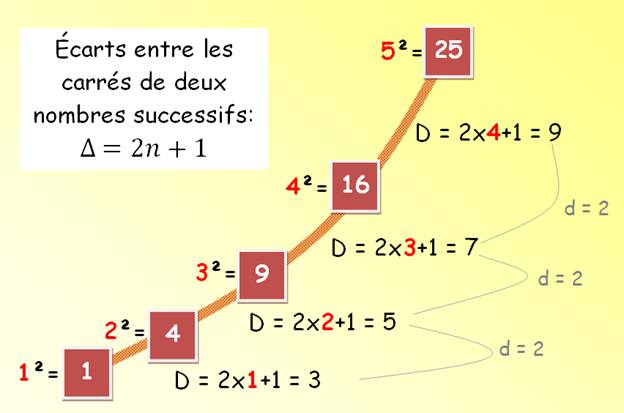
n et n+1 (n+1)² – n² = 2n + 1 n et n–1 n – (n–1)² = 2n – 1 n et n+10 (n+10)² - n² = 20n + 100 |
Exemple
Calculs rapides 91² = 8
100 + 180 + 1 = 8 281 51² = 2
500 + 100 + 1 = 2 601 99² = 10 000 – 200 + 1 = 9 801 59² = 3
600 – 120 + 1 = 3 481 17² = 49
+ 140 + 100 = 289 26² = 256
+ 320 + 100 = 876 |
|
|
Illustration
|
||
Voir Découverte
Junior du calcul mental des carrés (fichier .ppt)
|
|
|||||||||||
|
D
/ U |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0. |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
||
|
1. |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
33 |
35 |
37 |
|
|
2. |
39 |
41 |
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
|
|
3. |
59 |
61 |
63 |
65 |
67 |
69 |
71 |
73 |
75 |
77 |
|
|
4. |
79 |
81 |
83 |
85 |
87 |
89 |
91 |
93 |
95 |
97 |
|
|
5. |
99 |
101 |
103 |
105 |
107 |
109 |
111 |
113 |
115 |
117 |
|
|
6. |
119 |
121 |
123 |
125 |
127 |
129 |
131 |
133 |
135 |
137 |
|
|
7. |
139 |
141 |
143 |
145 |
147 |
149 |
151 |
153 |
155 |
157 |
|
|
8. |
159 |
161 |
163 |
165 |
167 |
169 |
171 |
173 |
175 |
177 |
|
|
9. |
179 |
181 |
183 |
185 |
187 |
189 |
191 |
193 |
195 |
197 |
|
|
|
||
|
2² = 4 8² = 64 22² = 484 68² = 4 624 78² = 6 084 92² = 8 464
0² = 0 => 0 1² = 1 => 1 10² = 100
=> 1 10² = 100
=> 1 9² = 81 => 9 90² = 8 100 =>
9 18² = 324
=> 9 45² = 2 025 =>
9 19² = 361
=> 10 46² = 2 116 => 10 55² = 3 025 => 10 99² = 9 801 => 15 |
N mc du 0 0 0 10 1 0 20 4 0 30 9 0 40 16 0 50 25 0 60 36 0 70 49 0 80 64 0 90 81 0 1 0 1 49 24 1 51 26 1 99 98 1 2 0 4 48 23 4 52 27 4 98 96 4 3 0 9 47 22 9 53 28 9 97 94 9 4 0 16 46 21 16 54 29 16 96 92 16 11 1 21 39 15 21 61 37 21 89 79 21 18 3 24 32 10 24 68 46 24 82 67 24 5 0 25 15 2 25 25 6 25 35 12 25 45 20 25 55 30 25 65 42 25 75 56 25 85 72 25 95 90 25 23 5 29 27 7 29 73 53 29 77 59 29 6 0 36 44 19 36 56 31 36 94 88 36 21 4 41 29 8 41 71 50 41 79 62 41 12 1 44 38 14 44 62 38 44 88 77 44 7 0 49 43 18 49 57 32 49 93 86 49 16 2 56 34 11 56 66 43 56 84 70 56 19 3 61 31 9 61 69 47 61 81 65 61 8 0 64 42 17 64 58 33 64 92 84 64 13 1 69 37 13 69 63 39 69 87 75 69 24 5 76 26 6 76 74 54 76 76 57 76 9 0 81 41 16 81 59 34 81 91 82 81 22 4 84 28 7 84 72 51 84 78 60 84 17 2 89 33 10 89 67 44 89 83 68 89 14 1 96 36 12 96 64 40 96 86 73 96 |
|
Point de situation
|
Nous savons calculer mentalement tous les
carrés de 1 à 100. Il serait illusoire que cela est facile
et ne demande pas d'effort. Un entraînement est nécessaire. C'est un
excellent exercice pour entretenir les neurones! Dans un exercice de récitation des carrés
des nombres successifs, il est possible et conseillé d'utiliser la tactique
la plus appropriée selon le nombre à porter au carré: terminé par 0, par
1 … et la tactique du calcul de la
différence a toute sa place pour vérifier et même calculer. Nous pouvons même
en faire une stratégie de calcul pour tous les nombres. C'est l'objet de la
page suivante. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()