|
|||||||||||||||||||||||||||||||||||
![]()
|
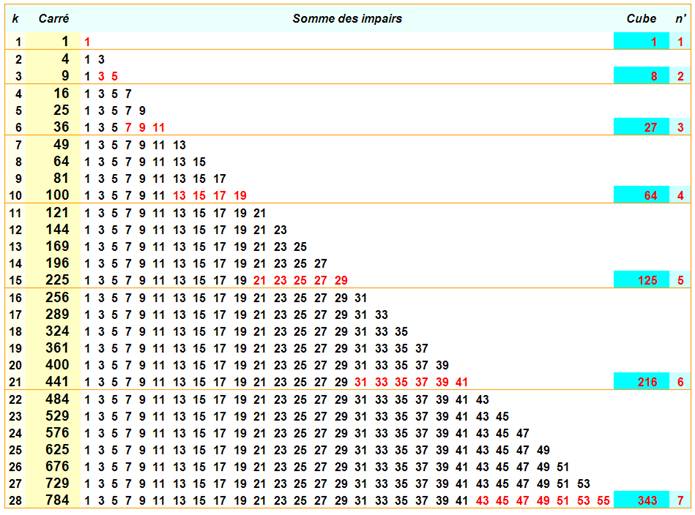
SOMME des ENTIERS IMPAIRS Tables Rappel La somme des k premiers
impairs est égale au carré de k. 1 + 3 + 5 + … +
(2k – 1) = k² Exemple avec k = 4: S = 1 + 3 + 5 +
7 = 4² Exemple
de propriétés
|
|
& CARRÉS ET CUBES |
|
|
Commentaires
de 441
= … + 41
|
|
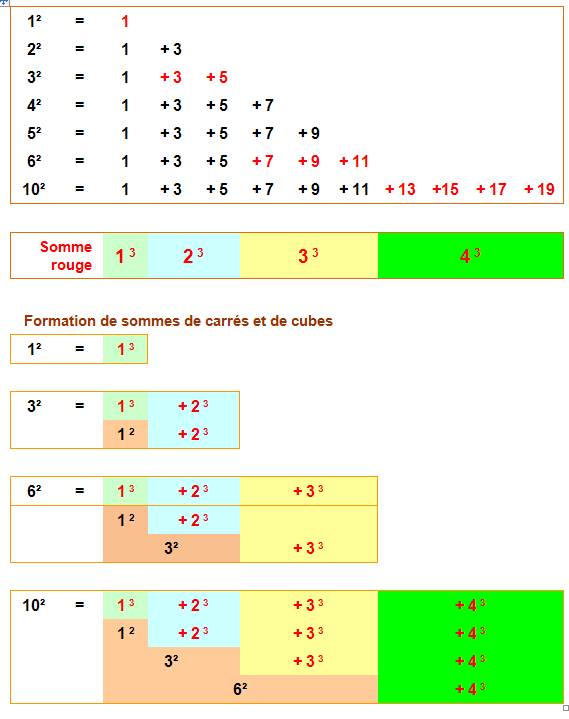
Voir Calcul des
plages pour les cubes / Somme de cubes et
carrés
|
IMPAIRS,
CARRÉS ET CUBES |
|
|
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()