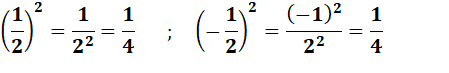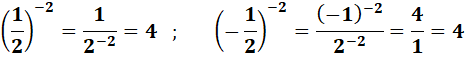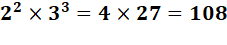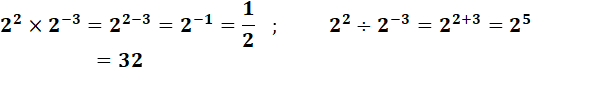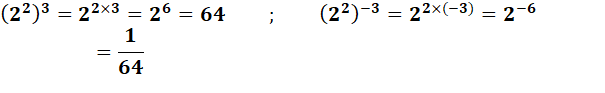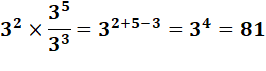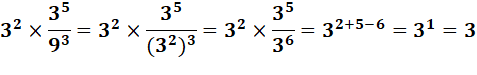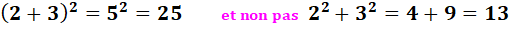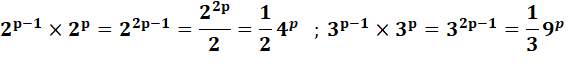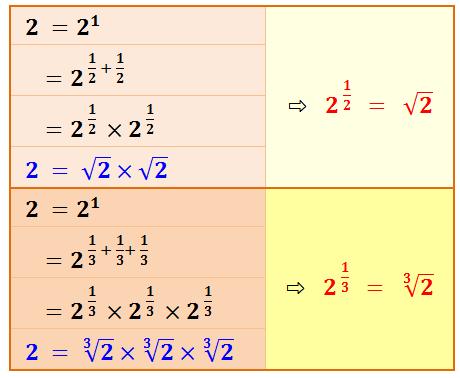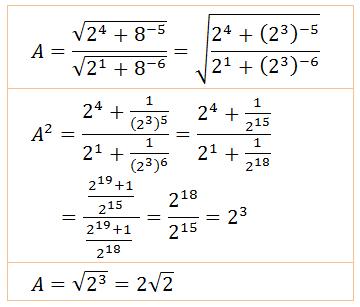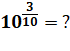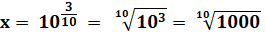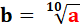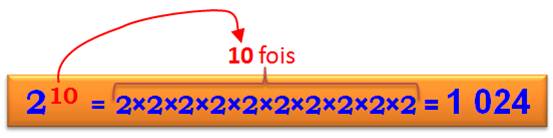
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/02/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	EXPOSANTS
Débutants Général	PUISSANCES & RACINES						Glossaire Puissance
INDEX Puissances	Puissance		Chiffres		Comparaison	Puissance de 2
	Racine		Racine carrée		Continue	Racine de 2
	Arithmétique			Algèbre	Négatif & Fract.	Étages
	Exercices
		Sommaire de cette page >>> Approche >>> Expériences avec les puissances de 2 >>> Expérience sur quelques puissances >>> Propriétés >>> Somme des chiffres >>> Remarques sur la forme des puissances >>> Exemples de calculs simples >>> Fractionnaires >>> Fractionnaires ou radicaux? >>> Calculs >>> Exposant décimal >>> Anglais >>> Curiosité >>> Bilan – Puissance, exposant et indice

PUISSANCES d'un nombre

Notation particulièrement astucieuse et puissante qui s'expose à être très utilisée.

La puissance s'exprime par le petit nombre en haut à droite,

comme avec 2¹⁰ , qui vaut 2 multiplié dix fois par lui-même.

Notez que 2¹⁰ commence par 10 (un bon moyen pour le retenir).

À défaut de pouvoir mettre un exposant, on note 2¹⁰ par 2^10 ou encore 2 E10.

Vous connaissez déjà des puissances: l'aire du carré est égale à c² = c x c (c au carré ou c à la puissance 2)

Voir Nombre 1024

Math-métaphysique

Voir Religions

APPROCHE

Puissances de 10

10	1 suivi de 1 zéro	10^1
100	1 suivi de 2 zéros	10^2
1000	1 suivi de 3 zéros	10^3
100 … 0	1 suivi de n zéros	10^n

Autre façon de voir

10	= 10	1 fois 10	10^1
100	= 10 x 10	2 fois 10 par lui-même	10^2
1000	= 10 x 10 x 10	3 fois 10 par lui-même	10^3
100 … 0	= 10 x 10 x …..x 10	n fois 10 par lui-même	10^n

Puissances de 2

2	= 2	1 fois 2	2^1
4	= 2 x 2	2 fois 2 par lui-même	2^2
8	= 2 x 2 x 2	3 fois 2 par lui-même	2^3
	= 2 x 2 x …..x 2	n fois 2 par lui-même	2^n

Notation

Dans 2 ⁿ , n est appelé l'exposant.

On lit 2 exposant n ou, plus classiquement, 2 puissance n.

Voir Tracas de calculs avec les puissances

EXPÉRIENCES avec les PUISSANCES de 2

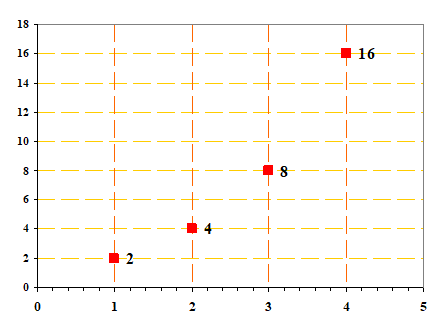
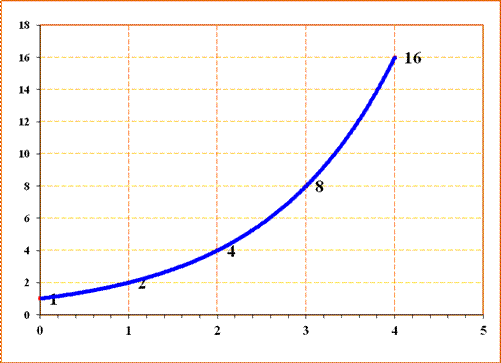
Illustration montrant la progression des puissances de 2 On montre les valeurs successives des puissances de 2: Remarquez d'abord que: produit des nombres: 2 x 4 = 8 sommes des exposants: 2^1 x 2^2 = 2^1+2 = 2^3 Courbe On dessine la courbe qui rejoint ces points: Question Si 2^3 = 8 et 2^4 =16, on est alors tenté de se demander ce qu'il se passe entre les deux. Est-ce qu'il existe, par exemple: une puissance 2^3,5 ? une puissance de 2 qui correspond 12 ? Réponse: Oui ! On généralise ce qui n'était qu'une notation en une fonction. On obtient, par exemple: 2^3,5 = 11,3 12 = 2^3,585 Généralisation En fait, on peut prendre la puissance quelconque d'un nombre quelconque a^b. 10^3,5 = 3162,2… 2,5^3,5 = 24,7… 12^21 = 460 05119 90936 97014 66112 = 0,46 … 10^23 123^321 = 0,72 … 10^671 Ça grimpe vite ! C'est justement un des intérêts de cette notation. Nommer de très grands nombres à l'aide de nombres plus courts.

Voir Prolongement pour les puissances négatives

Expérience étonnante sur quelques puissances
Petites valeurs de n Notez la progression fulgurante de n^3. Alors que n^2 et 2^n se disputent au départ, c'est 2^n qui l'emporte.	Grandes valeurs de n On a vu que n^3 est parti sur les chapeaux de roue. Mais, c'est 2^n qui l'emporte sur la distance.
Conclusion: attention à bien analyser une fonction avant de conclure.

PROPRIÉTÉS

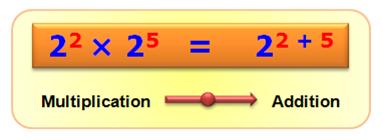
Fondamentale

Le produit des puissances (x et y) d'un nombre (a) est égale à la puissance somme (x + y) de ce nombre: a^x . a^y = a^{x + y}

En effet, par exemple:

a² = a . a

a³ = a . a . a

a² . a³ = a .a . a. a . a = a⁵ = a ^{2 + 3}

Exemples d'applications

a^x . a^y . a^z	=	a^x + y + z
a^4 . a^2 . a^5	=	a^4 + 2 + 5	= a^11

a^x = a^x + 0	=	a^x. a^0	=> a^0 = 1
a^n. a^-n	=	a^n – n= a^0 = 1	=> a^–n= 1 / a^n

Autres formules

Suite POSTER – Lois des exposants

À bien noter:

Une puissance négative est une puissance positive au dénominateur: 2^-2 = 1 / 2² et

Une puissance fractionnaire est une racine: 2^1/2 = .

Exemples

3^8 / 3^5	=	3^8 - 5	= 3^3
5^3 / 5^6	=	5^3 - 6	= 5^-3

( 5^3 ) ^2	=	5^3 . 2	= 5^6
( 5 . a ) ^2	=	5^2 . a^2	= 125 . a^2
( 5 / 2 ) ^5	=	5^5 / 2^5	= 3125 / 32
2^-3	=	1 / 2^3	= 1/ 8
8^-1 / 3	=	1 / 8^1/3	= 1/ (2^3)^1/3 = 1/ 2^3/3 = 1/2

Valeurs

a^0 10^0	= =	1 1
a^1 10^1	= =	a 10

Voir Valeurs avec des zéros

▲Prudence avec les nombres négatifs▲

a ^{(x . y)} = (a ^x ) ^y

Pour que la formule soit exacte, il faut que a soit positif.

En effet, contre-exemple avec a = (-1):

(-1) ^{(2 . 1/2)} = (-1) ¹ = - 1

( (-1) ² ) ^1/2 = ( 1 ) ^1/2 = 1

Notation – Historique

On doit à John Wallis la notation avec les exposants:

Merci à Lionel Watrin

Voir Brève 588 – Puissances négatives / Brève 589 – Puissances fractionnaires

Le zéro qui donne 1

Comment montrer logiquement que

2⁰ = 1, comme a⁰ = 1

Voir Nombre 0

Somme de chiffres – Exemple d'application
Problème Calculez la somme des chiffres de ce produit: 5^2015x 2^2018 Indice Les nombre 5 et 2 font penser immédiatement à 2 x 5 = 10. Propriétés utilisées 2^a+b = 2^a x 2^b 5^a x 2^a = 10^a	Calcul 5^2015x 2^2018 = 5^2015x 2^2015 x 2^3 = 10^2015 x 2^3 = 100…02015 x 8 = 800…02015 Somme des chiffres S = 8 + 0 + 0 + … = 8
Notez que l'on trouverait le même résultat avec ce cas simple ou sa généralisation: Exemple a = 2, k = 10 5^2 x 2^12 = 102 400 S = 1 + 0 + 2 + 4 = 7	Cas simple 5^5x 2^8 = 10^5 x 2^3 => S = 8 En effet: 5^5x 2^8 = 800 000 Généralisation 5^ax 2^a+3 = 10^a x 2^3 => S = 8 5^ax 2^a+k = 10^a x 2^k => S = somme des chiffres de 2^k

Remarques sur la forme des puissances

Il n'y a pas de carré de la forme 3n – 1. Il n'y a pas de nombre triangulaire de la forme 3n – 1. Tout cube est de la forme 9n + t avec t = -1 , 0 ou 1. Le reste de la division par 7 d'un cube est 0, 1 ou 6. Si un nombre est à la fois carré et cube, il est de la forme 7n ou 7n + 1. Quels que soient a et x, a^x + a et a^x – a sont toujours pairs. Toute puissance paire d'un nombre impair est de la forme 8r + 1. Toute puissance 12^e d'un nombre est de la forme 13n ou 13n + 1. Toute puissance 8^e d'un nombre est de la forme 17n + t avec t = -1, 0 ou 1.

Exemples de calculs simples
(La puissance zéro met à 1) (La puissance 1 laisse en l'état) Attention Se souvenir que puissance k veut dire que le produit est répété k fois.

Voir Déjouer les principaux pièges / Puissances de dix / Formation des nombres

Transformation avec les produits du nombre ou de l'exposant

8⁶ = 2⁶ x 4⁶ = 2⁶ x 2⁶ x 2⁶

= 8³ x 8³ = 2³ x 4³ x 2³ x 4³ = 2³ x 2³ x 2³ x 2³ x 2³ x 2³

= 262 144

Transformation avec le double du nombre ou de l'exposant

Ex: 3⁶ = 9³ = 729

7⁶ = 49³ = 117 649
10¹⁰ = 100⁵ = 10 000 000 000

Voir Calculs avec nombres parfaits / Simplification de 100²⁰⁰ / 200¹⁰⁰ (Brève-1025)

Exposants FRACTIONNAIRES

Demi-mesure …

Maintenant que l'on sait jouer avec les puissances, faisons la même expérience avec les fractions.

Exprimons " 2 " de deux manières différentes (première ligne noire et dernière ligne bleue de chaque tableau):

La puissance fractionnaire est une racine.

Exemples de calcul

Méthode 1		Méthode 2
2^1,5 =	2^3 / 2 (2^1/2 ) ^3 (2 )^3 (1,414…)^3 2,828…	2^1,5 =	2^3 / 2 ( 2^3 ) 8 2,828…

Méthode 1		Méthode 2
2^1,5 . 2^2,5 =	2^3 / 2 . 2^5 / 2 (2 )^3 . (2 )^5 (2 )^3 + 5 (2 )^8 2^4 16	2^1,5 . 2^2,5 =	2^1.5 + 2.5 2^4 16

Notez, par exemple, la multitude de possibilités pour faire 16:

16 =	2^4
	2^1 . 2^3	= 2 x 8
	2^1,5 . 2^2,5	= 2,828… x 5,656…
	2^2 . 2^2	= 4 x 4
	2^1,821 . 2^2,179	= 3,533… x 4,528…
	2^0,333… . 2^3,666…	= 1,259… x 12,699…
	…
	2^a . 2^b	avec a + b = 4

Voir Exemple avec faire 233 avec quatre "4"

Puissances fractionnaires ou radicaux ?
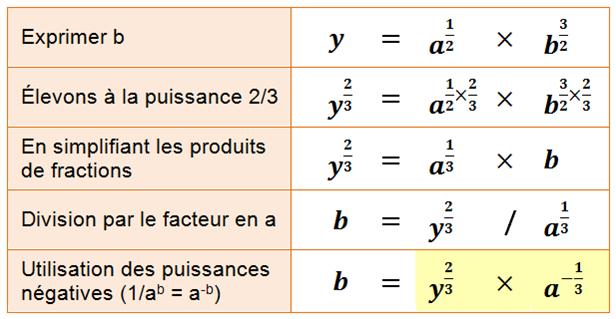
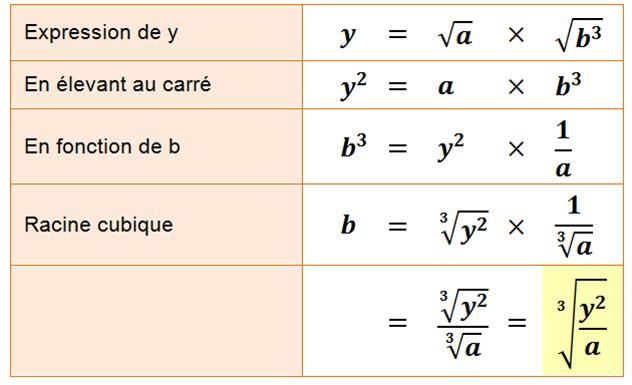
Voici un calcul exécuté sous les deux formes. Dans les cas les plus complexes, la forme fractionnaire est plus pratique. Exposants fractionnaires – Évaluez b Radicaux Bien retenir Exposant négatifs DIVISIONS Exposants fractionnaires RACINES Humour

Voir Exercices pratiques / Avec des racines cubiques

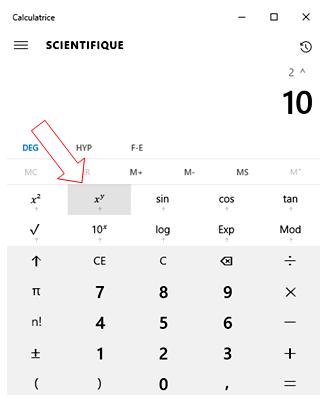
Calcul de puissance sur la calculette

Voir Calculette

CALCULS – Exemples

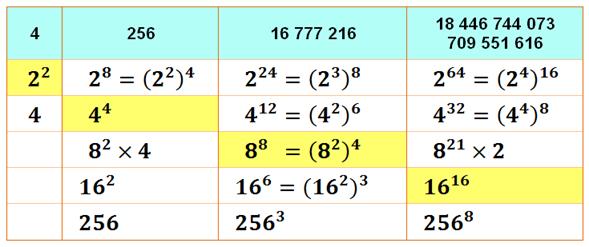
Mise en bouche

Exprimez 4⁴, 8⁸ , et 16¹⁶ selon les puissances de 2, 4, 8 …

Égal 1

Énoncé	Solution
Simplifiez 2^n . 4^-2n . 8^n	On évalue 2^n . 4^-2n . 8^n = 2^n . (2²)^-2n . (2^3)^n = 2^n . 2^-4n . 2^3n = 2^n - 4n + 3n = 2^0 = 1
Énoncé	Solution
Si a = b^x b = c^y c = a^z Montrez que x.y.z = 1	On évalue a = a^1 = b^x = (c^y)^x = [(a^z)^y]^x = a^x . y . z Conclusion x.y.z = 1
Énoncé	Solution
Évaluez (a^x )^y - z . (a^y )^z - x . (a^z )^x - y	On développe (a^x )^y - z . (a^y )^z - x . (a^z )^x - y = a^xy ^- xz . a^yz -yx . a^zx - zy = a^xy - xz + yz -yx + zx - zy = a^0 = 1

Voir Nombre 1

Comparaisons

Énoncé	Solution
Comparez Sans calculer les valeurs ^43 ^65	Évaluons chaque terme ^43 = 3^1/4 = 3^3/12 = ^1227 ^65 = 5^1/6 = 5^2/12 = ^1225 Conclusion ^1227 > ^1225 ^43 > ^65 Pour vérification ^43 = 1, 316… le plus grand ^65 = 1, 307…
Énoncé	Solution
Comparez Sans calculer les valeurs ^310 5	Évaluons chaque terme ^310 = 10^1/3 = 10^2/6 = ^6100 5 = 5^1/2 = 5^3/6 = ^6125 Conclusion ^6100 < ^6125 ^310 < 5 Pour vérification ^310 = 2, 15… 5 = 2, 23 le plus grand

Exercice bonus

Valeur de √(2^4 + 8^(-5)) / √(2^1 + 8^(-6))

Calcul de cette expression pas à pas

Mettant à contributions les principales règles de composition des puissances

À noter ce rapprochement entre fractions – Étonnant!

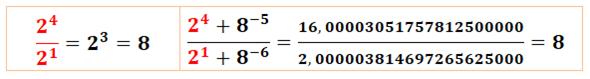
Voir Nombre 8

Exposant décimal
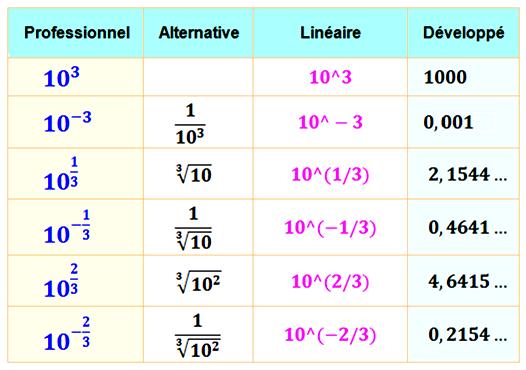
Exemple: calculez 10^0,3 La calculette donne un nombre proche de 2.	10^0,3 = 1,9952623149…
Interprétation En fait: 0,3 = 3/10 Nous cherchons donc un nombre tel que multiplié dix fois par lui-même, il donne 1000. Sachant que 2^10 = 1024, on sait que le nombre cherché est légèrement inférieur à 2.	Au numérateur, c'est une puissance. Au dénominateur, c'est une racine.
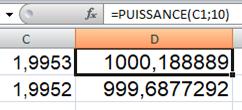
Avec un tableur On procède par dichotomie. Deux lignes de calcul, on ajoute des chiffres un par un en maintenant les résultats de part et d'autre de 1000.	En D1: instruction puissance 10 de C1 En D2: instruction puissance 10 de C2

Comment calculer la valeur? On passe par les logarithmes, puis son inverse, l'exponentielle	x = 10^0,3 log(x) = 0,3 log(10)
Comment calculer cette valeur? Avec le développement en séries	Avec x = 0,69077
Calculs Il faut calculer jusqu'au dixième terme pour obtenir 10 chiffres significatifs en conservant 12 décimales tout le long du calcul. Vive la calculette.	1, 1,690775528 2, 1,929360943 3, 1,984297265 4, 1,993784432 5, 1,995095133 6, 1,995246033 7, 1,995260924 8, 1,995262210 9, 1,995262307 10, 1,995262314

Autre exemple

Quelle est la valeur de:			2^0,1 = ?
Nombre rationnel* en fraction			0,1 = 1/10
Retour			2^0,1 = 2^1/10
Somme des exposants => produit	2 = 2^1 = 2^10/10 = 2^1/10 + 1/10 + … +1/10 = 2^1/10 x 2^1/10 x … x 2^1/10 (10 fois)
Rappel Définition de la puissance		a = b.b.b.b.b.b.b.b.b.b = b^10
Définition de la racine (inverse de la puissance)
Dans notre cas

* Généralisation possible pour les irrationnels. Voir mon explication via les log et exponentielles

Exemple général

Quelle est la valeur de:	2^2,34
Quelle est la fraction pour 2,34	2,34 = 117 / 50
Retour à notre nombre	2^2,34 = 2^117 / 50
Avec exposant fractionnaire = racine
Détail Le nombre 5,0630 multiplié 50 fois par lui-même donne ce grand nombre à 35 chiffres qui vaut 2 puissance 117 Nous avons  bien calculé la racine 50^e de la puissance 117 de 2 ou autrement-dit la puissance 2,34 = 117/50 du nombre 2.

Curiosités numériques

81 = 9¹⁺¹, seule solution de AB = C^B+1.

Autres possibilités

K	AB	=	C^B + K
1	81		9	^1+1
2	64		2	^4+2
3	81		3	^1+3
3	32		2	^2+3
K	DAB	=	C^B + K
2	243		3	^3+2
2	256		2	^6+2
0	343		7	^3+0
7	512		2	^2+7
1	512		8	^2+1

English corner

Exposant	Index, pluriel indices or exponent
Mantisse	Mantissa
Radicaux	Surds
Virgule flottante	Floating-point

The exponent of a number says how many times to use the number in a multiplication.

In words: 8² could be called "8 to the power 2" or "8 to the second power", or simply "8 squared".

In words: 5³ could be called "5 to the third power", "5 to the power 3" or simply "5 cubed".

Source anglais: Exponents - Maths is fun

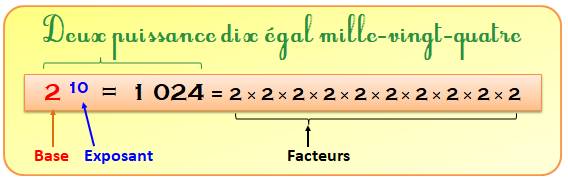
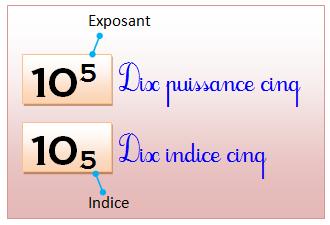
Bilan – Puissance, exposant et indice

Les exposants sont une forme d'écriture des puissances, bien pratique car il est possible de calculer simplement avec les exposants.

Lorsqu'on écrit 10 avec un petit 5 en haut à droite, on lit dix à la puissance 5. Le petit chiffre est l'exposant. Placé en bas à droite, il devient un indice.

Résumé des formes possibles des puissances et de leurs écritures

Question de vocabulaire: puissance ou exposant

L'exponentiation étend la notion de puissance en algèbre. Pour rendre compte de cela, certains emploie le vocable "dix exposant trois" au lieu de "dix puissance trois" ou "dix à la puissance trois". Cet usage n'est pas recommandé!

En fait "dix exposant trois" peut se dire, mais pour exprimer une notion particulière introduite explicitement par l'auteur du texte; mais s'il s'agit d'une puissance, on dit bien (et uniquement), en abrégeant de plus en plus:

dix élevé à la puissance trois ou

dix à la puissance trois ou

dix puissance trois.

Certains disent "dix exposant trois" et comme le dit Wikipédia, il s'agit d'un usage abusif. Ce n'est même pas un anglicisme, car les Anglo-Saxons disent aussi "ten to the power three", dix à la puissance trois.

Les exemples d'emploi de l'exposant autres que pour la puissance ne sont pas nombreux. Par contre, avec l'indice, il en existe de multiple: n indice 3 veut dire aussi bien le nombre n exprimé en base 3 ou encore le n, troisième du nom dans une énumération, etc.

Même pour la notation des combinaisons, qui nécessite indice et exposant, on dit "C deux trois" et non "C indice 2 exposant 3".

Il serait tentant d'uniformiser "10 exposant trois" comme on dit "dix indice trois". Cette symétrie de langage ne reflèterait pas la dissymétrie mathématique. Si l'indice avait un usage unique, il est à parier qu'il aurait lui-aussi un nom.

Voir DicoMot Maths: Puissance / Notation scientifique des nombres / Nombres index

Suite	Exposants - Exercices pratiques Notation scientifique Unité des puissances Chiffres dans les puissances Somme des puissances des chiffres de nombres à deux chiffres
Voir	Calculs avec des racines cubiques Exponentielles Exposants – Index Limites de la fonction puissance Logarithmes Priorité des opérations Puissances de 10 Puissances de 2 Théorie des nombres – Index Zéro et infini
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/Puissanc.htm