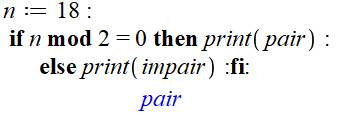|
||||||||||||||||||||||||||||||||
![]()
|
Un nombre pair
ne commet jamais d'impair (?!.) |
Voir Pensées
& humour / Devinette
|
NOMBRES PAIRS & IMPAIRS |
|
|
Rien de
plus simple que la division par 2. Et
pourtant de quoi faire quelques exercices utiles pour la suite. |
EVEN &
ODD Pair & Impair En
Anglais |
|
Les animaux ont
un nombre pair de
pattes. Les végétaux
sont plutôt portés sur l'impair. Le monde est fait de dualités. |
NEVER ODD
OR EVEN Jamais impair ou pair Voir
Palindrome |

Voir Pépites
![]()
Oups! Je
débute … >>>
|
|
|||
|
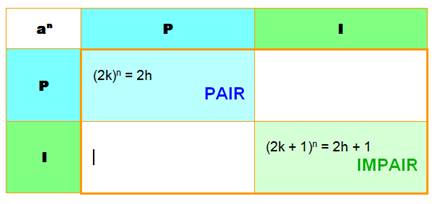
Pair |
Formule |
Exemple |
|
|
On peut dire aussi: un nombre
multiple de 2. |
n = 2.k |
6 = 2 x 3 |
|
|
Impair |
|||
|
On peut
dire aussi: un nombre qui succède à un nombre pair. |
n = 2.k + 1 |
7 = 2 x 3 + 1 |
|
|
Ces deux
formules sont la clé des propriétés des nombres pairs & impairs. Notations
Voir Nombres
premiers |
|||
|
|
||
|
Calcul détaillé
|
Résumé
Exemple
|
|
|
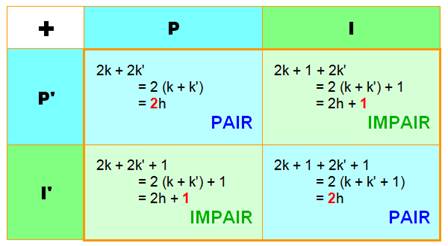
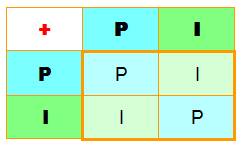
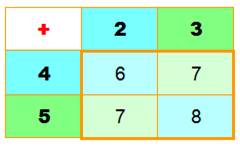
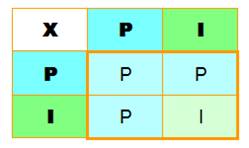
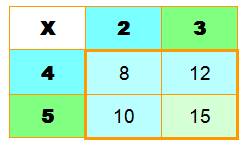
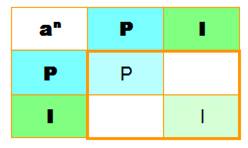
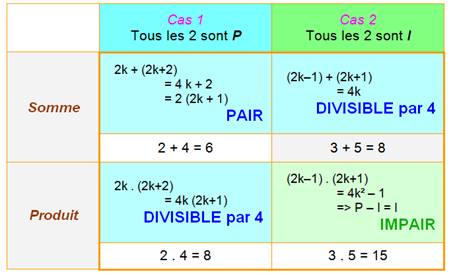
L'addition de
deux nombres de même parité donne une
somme paire. À
rapprocher du OU EXCLUSIF en logique >>> |
||
Voir Impairs sommes d'impairs / Énigme des trois verres et dix
pièces
|
|
||
|
Calcul détaillé
|
Résumé
Exemple
|
|
|
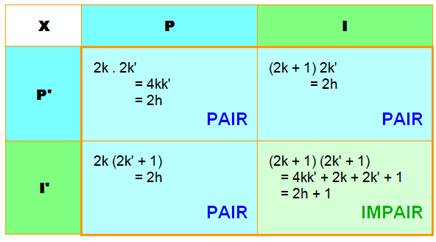
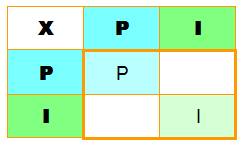
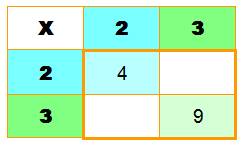
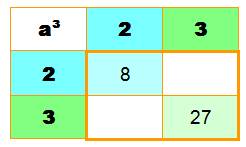
Seule la
multiplication de deux nombres impairs donne un produit impair. À rapprocher
du ET en logique >>> |
||
|
Cas particulier des carrés ou du produit de deux nombres de
même parité Un nombre élevé au carré conserve sa parité. |
Résumé
Exemple
|
|
|
|
|||
|
Nombre Son carré |
N = N² = |
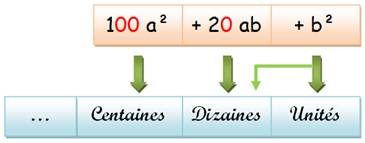
10a + b 100a² + 20ab + b² |
|
|
Place des
chiffres |
Les zéros entraînent le
positionnement indiqué. Pour les
dizaines, ne pas oublier la retenue provenant de la dizaine du carré de
l'unité. |
||
|
Si b est impair Chiffre des unités de N |
1² = 3² = 5² = 7² = 9² = |
01 09 25 49 81 |
Unité impaire |
|
Chiffre des dizaines de N |
20 ab dizaine de b² Somme Bilan |
pair paire paire |
cf. multiplication par 20. Constat ci-dessus. Car pair +pair = pair Dizaine paire |
|
Nombre impair au carré: unité impaire
et dizaine paire. |
|||
|
Si b est pair Chiffre des unités de N |
0² = 2² = 4² = 6² = 8² = |
00 04 16 36 64 |
Unités paires {0,
4, 6} |
|
Chiffre des dizaines de N |
|
|
Aucune conclusion |
|
|
||
|
|
|
|
|
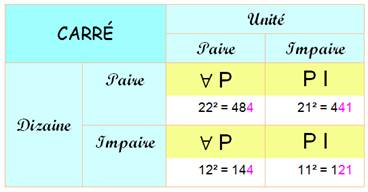
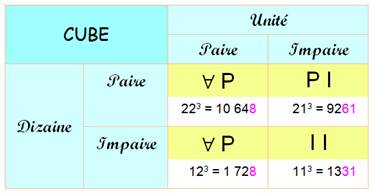
Note: le A renversé indique que le chiffre des dizaines
est quelconque (indéterminé). Nombre pair
au carré ou au cube Nombre impair
au carré ou au cube
dizaine toujours paire … sauf pour le cube d'un nombre avec
dizaine impaire. |
||
Voir Unités des puissances / Dizaines des puissances
|
des
nombres pairs et impairs |
|
|
|
Pairs |
Impairs |
|
|
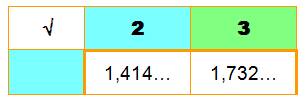
N = 2 k N² = 4 k² Divisible par 4 Exemples 10² = 100 = 4 x
5² 8² =
64 = 4 x 4² |
N = 2 k + 1 N² = 4 k (k + 1)
+ 1 Division par 4,
reste 1 Le terme en 4
est un produit comportant k et son successeur. Exemples 5² =
25 = 24 + 1 = 4 x 2 x 3 + 1 11² = 121 = 120
+ 1 = 4 x 5 x 6 + 1 |
|
|
Reprenons la
formule: N² – 1= 4 k (k + 1)
Ce nombre est
déjà divisible par 4. Il est aussi le produit de deux nombres successifs;
donc, l'un est pair; et, le produit est divisible par 2. Si bien que: N² – 1 est un nombre divisible par 8 (N impair).
Voir Carré et produit de
quatre consécutifs Démonstration
alternative Avec une identité remarquable: N² – 1 = (N – 1)
(N + 1) N étant impair,
N – 1 et N + 1 sont pairs. Et, étant
consécutifs, l'un est divisible par 4. L'un en 2k et
l'autre en 4k', le produit est en 8 kk'. Exemples 5² – 1
= 25 – 1 =
3 x 8 = 4 x 6 11² – 1 = 121 – 1
= 15 x 8 = 10 x 12 Les
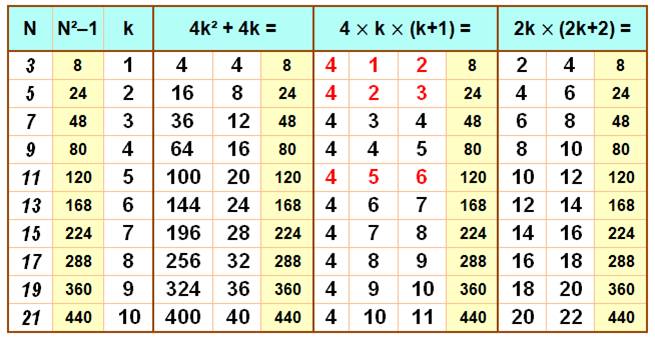
trois écritures N = 2k + 1 alors N² – 1 = 4k² + 4k = 4k (k + 1) = 2k (2k + 2) Tableau pour les nombres impairs de 3 à 21
En rouge, quelques produits à noter comme: 1 + 2 x 3 x 4 =
5² |
Voir Divisibilité des carrés et
des cubes / Divisibilité
par 8 / Divisibilité
par 24 / Divisibilité des
formes / Pépites numériques
|
|
||
|
Calcul détaillé
|
Résumé
Exemple
|
|
|
Un nombre élevé à une puissance
conserve sa parité. |
||
|
|
||
|
Calcul détaillé
|
Exemple
|
|
|
Aucune
conclusion possible avec la racine carrée d'un nombre quelconque. |
||
|
|
|
|
Deux nombres consécutifs Avec deux nombres consécutifs n
et n+1, l'un est pair l'autre est impair que ce soit dans
l'ordre ou non.
Opérations
La somme de
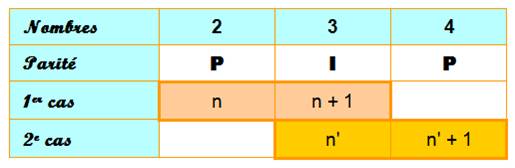
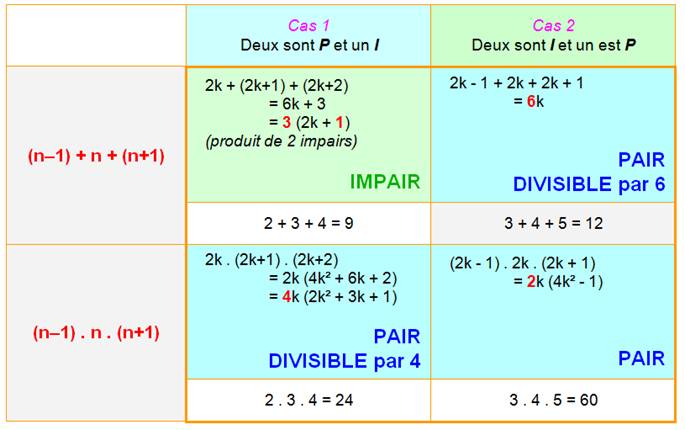
deux nombres consécutifs est impaire. Trois nombres consécutifs Avec trois nombres n – 1 , n et n + 1, il y a deux cas:
Opérations
La somme de trois nombres consécutifs est
de la même parité que celle du nombre initial de parité unique. Le produit de
trois nombres consécutifs est divisible par 2. Ou par 4, si deux d'entre eux sont pairs. Parmi trois nombres consécutifs, l'un d'eux
est pair au moins et l'un d'eux est
divisible par 3. Conclusion: Le produit de
trois nombres
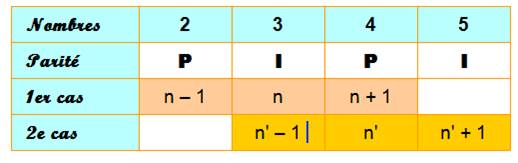
consécutifs est divisible par 6. Quatre nombres consécutifs Parmi quatre nombres consécutifs, deux sont
pairs et deux sont impairs. La somme
de quatre nombres consécutifs est paire. Le produit de
quatre nombres consécutifs est divisible par 24 = 4!. |
|
|
|
||
|
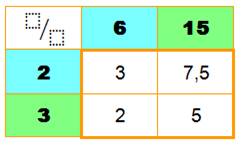
Deux nombres distants de 2 unités sont tous
les deux: soit pairs, soit impairs. Calcul détaillé
|
Conclusions La somme de deux nombres distants de 2 est
toujours paire.
Autrement dit: Cette
somme, divisée par 4, donne 0 ou 2 comme reste. Le produit de deux nombres distants de 2, divisé par 4
donne un reste de :
|
|
|
Bilan en tableau
|
||
|
|
|
|
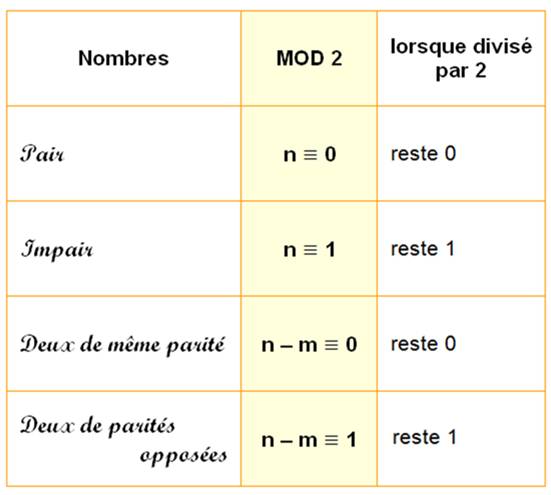
Notion de module (mod): on s'intéresse à ce
qui reste lorsqu'on retire des modules identiques à un nombre. C'est la division euclidienne, pour laquelle on ne retient que
les restes. On note ce fait avec un signe égal comportant trois traits. Ici, le module est égal à 2.
|
|
Voir
Introduction
au modulo / Application
aux triplets de Pythagore
|
|
|||
|
Si nous
pouvons détecter rapidement si un nombre est pair ou pair, comment faire dans
un programme informatique. |
Les
nombres pairs se terminent par (0,
2, 4, 6, 8). |
||
|
Détection par le reste de la
division par le 2. Utilisation
de la fonction modulo. |
Principe Si n mod 2 = 0 alors n est pair Sinon n est impair Maple
Python
|
||
|
Détection du dernier bit binaire. Cette
manière de faire ne change pas beaucoup l'écriture. Mais,
l'ordinateur manipulant des données en binaire, l'exécution est un peu plus rapide Voir application à la recherche des nombres
premiers Note: la fonction ET (AND en anglais)
est rendue ici par le symbole
"&". |
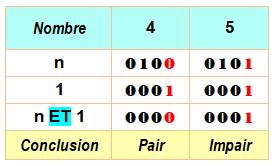
Principe Un ET entre un nombre binaire et le nombre 1
binaire est égal à 0 si n est pair et à 1 si n est impair. Exemple:
Python
|
||
Voir Programmation
– Index / Python
Voir
Expression en
anglais / Mnémotechnique
![]()
|
Nombres impairs |
|
|
|
n est un
nombre impair Divisé
par 2, il donne un reste de 1 Ce nombre
peut être positif ou négatif. Il appartient à l'ensemble des nombres relatifs
appelé Z. |
Exemples 7 est impair car 7 =
2 x 3 + 1 –7 est impair car –7 = –2 x 4 + 1 Écriture d'un nombre impaire en général n = 2k + 1 n et k sont positifs ou négatifs en même temps. Ce sont des nombres relatifs. Notations
|
|
|
Carré de n |
|
|
|
Ce
nombre, divisé par 2, donne 1 pour reste, c'est un nombre impair. On peut
dire aussi, le carré d'un nombre impair est de la forme 2K + 1, c'est un
nombre impair. |
Exemple 5² = 25 = 24 + 1 = 2 x 12 + 1 |
|
|
Cas de deux
nombres impairs On pose a
et b sous la forme de nombres impairs: un nombre fois 2 plus1. On
calcule le produit des deux que l'on essaie de mettre sous la forme d'un
nombre impair en 2K + 1 Le produit
de deux nombres impairs est un nombre impair. |
Deux nombres impairs a = 2k + 1 b = 2h + 1 Produit ab = (2k + 1)(2h +1) = 4kh + 2k + 2h + 1 = 2 (2kh
+ k + h) + 1 = 2 K + 1 |
|
![]()
|
Retour Suite |
|
|
Autour du sujet |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/PairImpa.htm |
![]()