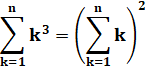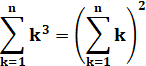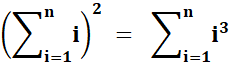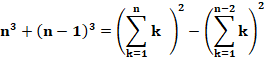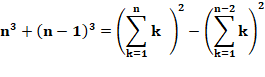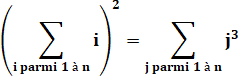NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/02/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Puissances
Débutants Logarithmes	Opérations sur les puissances		Glossaire Puissances
Rubrique PARTITION INDEX PUISSANCES	Somme de puissances
	Th de Pythagore	Th de Fermat-Wiles
	Démonstration du théorème	Carré somme de cubes
	Sommaire de cette page >>> Liste, programme et applications >>> Formules et exemples >>> Approche >>> Une belle suite d'identités >>> Théorème de Nicomaque de Gérase >>> Illustration >>> Démonstration muette >>> Méthode d'Abu Bakr al-Karaji >>> Démonstration par récurrence >>> Valeurs >>> Carré de somme = somme des cubes: consécutifs >>> Idem non-consécutifs >>> Cube de somme = somme des carrés >>> Carré de somme = somme des carrés >>> Cube de somme = somme des cubes

CARRÉ SOMME DE CUBES

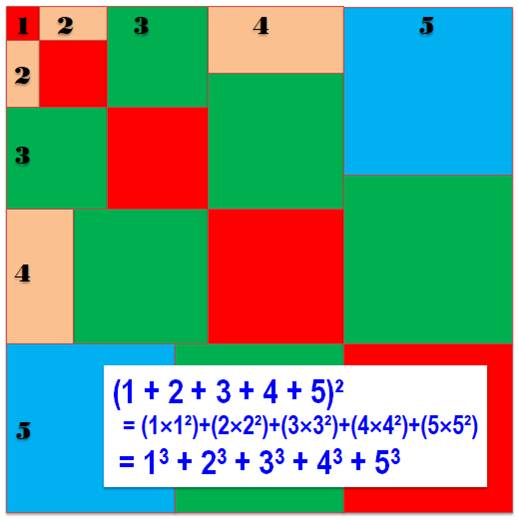
Théorème de Nicomaque

Un mariage des carrés et des cubes.

Avec les nombres successifs.

Exemple

C'est particulièrement joli ! Et ce n'est pas fini …

C'est la somme des nombres de notre table de multiplication.

C'est la quantité de rectangles dans une grille 9×9.

La formule de Faulhaber est une généralisation de cette formule.

Voir Carré = Somme de cubes / Somme de cubes consécutifs / Nicomaque

 Liste, programme et applications

Liste des nombres (∑n)² = ∑n^3 T² = ∑n^3	1, 9, 36, 100, 225, 441, 784, 1296, 2025, 3025, 4356, 6084, 8281, 11025, 14400, 18496, 23409, 29241, 36100, 44100, 53361, 64009, 76176, 90000, 105625, 123201, 142884, 164836, 189225, 216225, 246016, 278784, 314721, 354025, 396900, 443556, 494209, 549081, 608400, 672400, 741321, 815409, 894916, 980100, 1071225, 1168561, 1272384, 1382976, 1500625, 1625625… OEIS A000537 Notes: Aucun cube parmi ces nombres sauf 0 et 1 La somme des entiers successifs est un nombre triangulaire.
Programmes Maple	Version simple L := []; for n to 5 do S := add(i^3, i = 1 .. n); L := [op(L), S] end do; L; [1, 9, 36, 100, 225] Version avancée a := proc (n) options operator, arrow; (1/4)*n^2*(n+1)^2 end proc; seq(a(n), n = 0 .. 5); 0, 1, 9, 36, 100, 225
Applications Somme de tous les nombres de la table de multiplication jusqu'à n×n. Quantité de rectangles dans une grille de n×n carrés. Quantité de permutations de n éléments distincts, chacun présent deux fois avec n ou n – 4 éléments en bonne position (élément i en position i dans la liste)

Formules et exemples

Somme cube = carré somme nombre Cube = différence de carrés	1^3 + 2^3 + 3^3 = (1 + 2 + 3)^2 36 = 6² 3^3 = (1 + 2 + 3)² – (1^3 + 2^3) 27 = 36 – 9
Écriture informatique
Ce type de relations existe pour tous les cubes

Approche

Observation

9 = 3 x 3 = 1³ + 2³

Volume de la tour: 1 + 2³

Hauteur de la tour: 3

Surface occupée par les cubes de la tour, mis à plat :

1 + 8 = 9 = 3²

Tous les cubes se rangent dans un carré dont le côté est égal à la hauteur de la tour. Ce cas n'est pas particulier. Il est généralisable à toutes les tours.

Tour n°	Hauteur	Volume		Surface
1	1	1	=	1	=	1
2	3	1 + 2^3	=	(1 + 2)²	=	9
3	6	1 + 2^3 + 3^3	=	(1 + 2 + 3)²	=	36
4	10	1 + 2^3 + 3^3 + 4^3	=	(1 + 2 + 3 + 4)²	=	100
5	15	1 + 2^3 + 3^3 + 4^3 + 5^3	=	(1 + 2 + 3 + 4 + 5)²	=	225
…
n	n (n + 1)/2	1 + 2^3 + 3^3 + ... + n^3	=	(1 + 2 + 3 + ... + n)²

Une belle suite d'égalités et une formule
Carrés	Cubes	Total

Voir Nombre 36 / Nombre 100

Théorème de Nicomaque de Gérase

Somme cubes = carré ( 1 + 2 + 3 + … + n )^2 = 1^3 + 2^3 + 3^3 + … + n^3 La somme des cubes des nombres successifs est le carré de la somme de ces nombres Rappel (1 + 2 + 3 + … + n ) = Somme des entiers successifs = Nombres triangulaires = 1/2 n (n + 1) En remplaçant S = ( 1 + 2 + 3 + … + n )^2 = { 1/2 n (n + 1) }² = 1/4 { n²(n + 1)² } Formule générique S = ( 1 + 2 + 3 + … + n )^2 = 1^3 + 2^3 + 3^3 + … + n^3 = 1/4 (n^4 + 2n^3 + n^2 ) = 1/4 { n² (n+1)² } = Tn^2 En résumé Carré de la somme des nombres = carré du nombre triangulaire = somme des cubes.

ILLUSTRATION
Premier regard sur le grand carré Calcul de l'aire du grand carré Second regard sur le grand carré Calcul de l'aire de chaque équerre

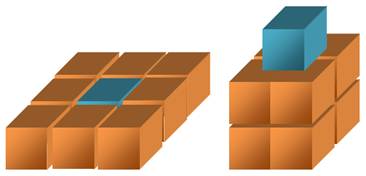
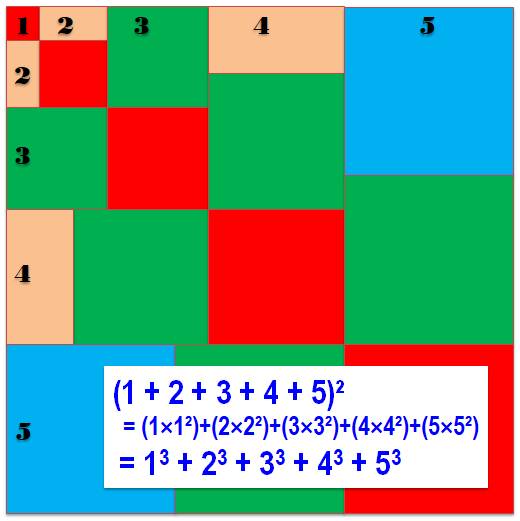
Carré = somme cubes: démonstration muette

Chaque carré-diagonale k² est accompagné de k carrés latéraux formant le cube.

Pour k = 2 et 4, le carré est composé de deux rectangles k x k/2

Voir Brève 591

Méthode d'Abu Bakr al-Karaji (vers 1019)

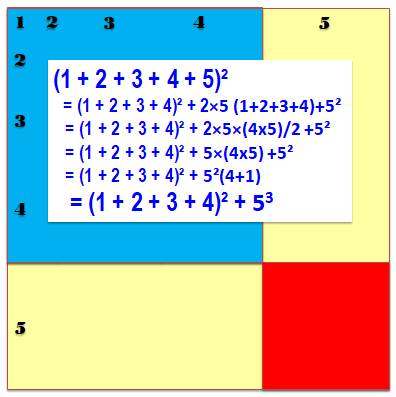
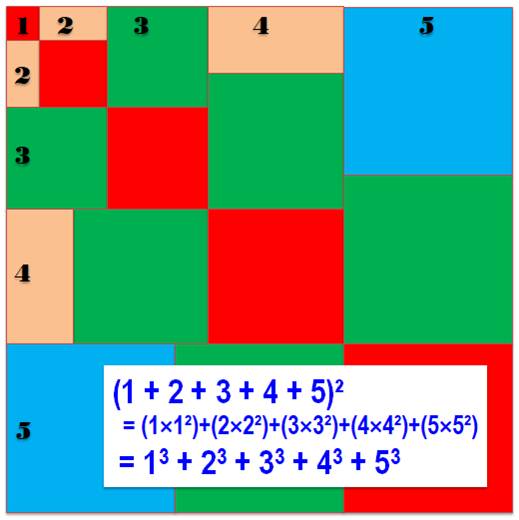
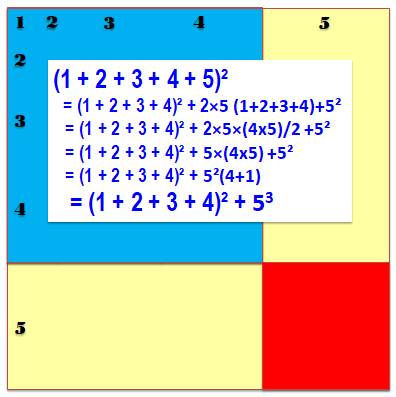
La figure permet d'établir une formule de récurrence reliant le carré de la somme S²(n) au carré de la somme S²(n-1) + n³.

Ici: (1 + 2 + 3 + 4 + 5)²

= (1 + 2 + 3 + 4)² + 5³

En reprenant la même formule pour n décroisant, on a successivement:

(1 + 2 + 3 + 4 + 5)² =
	(1 + 2 + 3 + 4)² + 5^3
	(1 + 2 + 3 )² + 4^3 + 5^3
	(1 + 2)² + 3^3 + 4^3 + 5^3
	(1 )² + 2^3 + 3^3 + 4^3 + 5^3
	1^3 + 2^3 + 3^3 + 4^3 + 5^3

On pourrait, évidemment, reprendre forme récurrent pour tout n.

Cube = Différence de carrés

La relation de récurrence permet d'établir cette relation:

Par exemple:

3³ = (1 + 2 + 3)² – (1 + 2)²

= 27 = 6² – 3² = 36 – 9

ou encore (dernière ligne):

20³ = (1+2+…+20)² – (1+2+…+19)²

= 8 000 = 210² – 190²

= 44 100 – 36 100

Notez que la même relation permet de définir d'autres égalités, comme:

Ex: 4³ + 3³ = (1+2+3+4)² – (1+2)²

= 64 + 27 = 100 – 9 = 91

Voir Exemple complet avec 216 dans l'en-tête

Voir Cube = Différence de carrés / Nombre 216 / Nombre 1000 / Brève 573

Démonstration par récurrence
Valeur de la formule pour n= 1
1^3	=	1²
On suppose l'égalité exacte
1^3 + 2^3+ 3^3+ ... + n^3	= =	(1 + 2 + 3 + ... + n )² { n (n + 1) / 2 }²
On ajoute (n+1)^3de chaque côté
1^3+ 2^3+ 3^3+ ... + n^3+ (n+1)^3	= =	(n (n+1)/2)² + (n+1)^3 ( (n+1) (n+2) / 2 )² Voir Détail du calcul
On retombe sur la formule pour n+1	=	(1 + 2 + 3 + ... + n + (n+1) )²
Conclusion: On a démontré que:	si la relation est vraie pour n , elle l'est aussi pour  n+1
Or, elle est vraie	pour n = 1
Donc	Elle est donc toujours vraie

Voir Démonstration par récurrence

Détail du calcul

Démonstration de la formule de base
Rappel de la formule pour n-1, n et n+1.	4 Sn-1 = (n - 1)² (n)² 4 Sn = (n)² (n + 1)² 4 Sn+1 = (n + 1)² (n + 2)²
Notre problème: supposant l'une des formules vraie, il faut démontrer la suivante. Choix de la formule: on imagine aisément qu'il sera plus facile de passer de n-1 à n que de n à n+1, car dans ce dernier cas, interviendrait (n+2) sans doute plus difficile à manipuler.
La formule est vraie pour n = 1 et même, si cela ne vous convainc pas, elle l'est aussi avec n = 2.	4 S1 = 1² x 2 ² = 4 = 4 ( 1^3 ) 4 S2 = 2² x 3 ² = 36 = 4 ( 1^3 + 2^3 )
Supposons la formule vraie pour n - 1 et calculons 4Sn	4 Sn = 4 (Sn-1 + n^3 )	= (n - 1)² (n)² + 4n^3
En développant Et apparaît la formule en Sn CQFD		= (n - 1)² (n)² + 4n. n² = (n² - 2n + 1 – 4n ) n² = (n + 1)² n²

Tableau donnant le total de la somme …

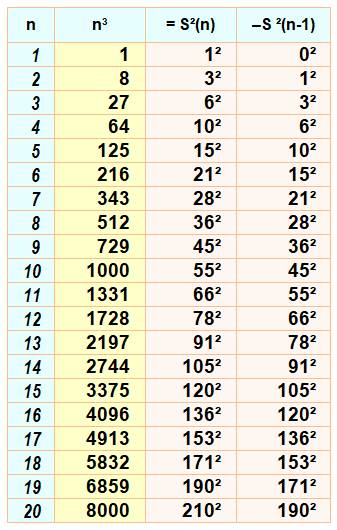
… du carré de la somme des entiers successifs, et par là-même

de la somme des cubes des entiers successifs

Exemples de lecture

Dizaines 0 et Unités 3 => S₃ = 1³ + 2³ + 3³ = 36 = (1 + 2 + 3)²

Dizaines 1 et Unités 3 => S₁₃ = 1³ + 2³ + … + 13³ = 8 281 = (1 + 2 + … + 13)²

Unités Dizaines	0	1	2	3	4	5	6	7	8	9
0	0	1	9	36	100	225	441	784	1296	2025
1.	3025	4356	6084	8281	11025	14400	18496	23409	29241	36100
2.	44100	53361	64009	76176	90000	105625	123201	142884	164836	189225
3.	216225	246016	278784	314721	354025	396900	443556	494209	549081	608400
4.	672400	741321	815409	894916	980100	1071225	1168561	1272384	1382976	1500625
5.	1625625	1758276	1898884	2047761	2205225	2371600	2547216	2732409	2927521	3132900
6.	3348900	3575881	3814209	4064256	4326400	4601025	4888521	5189284	5503716	5832225
7.	6175225	6533136	6906384	7295401	7700625	8122500	8561476	9018009	9492561	9985600
8.	10497600	11029041	11580409	12152196	12744900	13359025	13995081	14653584	15335056	16040025
9.	16769025	17522596	18301284	19105641	19936225	20793600	21678336	22591009	23532201	24502500
10.	25502500

Carré de somme = somme des cubes
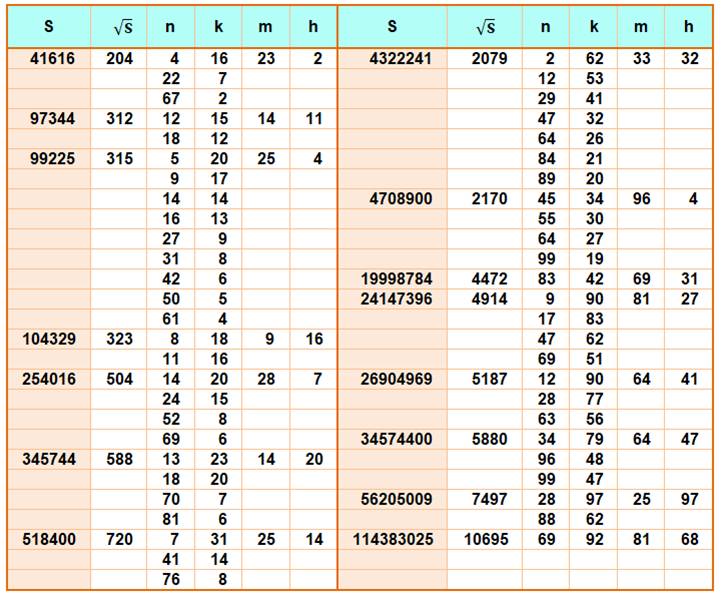
Nombres consécutifs de 1 à n	Toujours égalité comme vu ci-dessus	(1 + 2)^2 = 1^3 + 2^3 = 9
Nombres consécutifs de k à n	Aucune égalité	(3 + 4 + 5)^2 = 289 alors que 3^3 + 4^3 + 5^3 = 216
Quantité de termes différente avec même nombre de départ	Aucune égalité connue	(3 + 4)^2 = 49 alors que 3^3 + 4^3 + 5^3 = 216
Quantité de termes différente avec nombre de départ différents	Infinité d'égalités avec souvent plusieurs formes du carré	(4 + 5 + … + 20)^2 = (22 + 23 + … + 29)^2 = (67 + 68 + 69)^2 = 23^3 + 24^3 +25^3 = 41 616 Suite sur tableau ci-dessous

Carré de somme de consécutifs = somme de cubes consécutifs
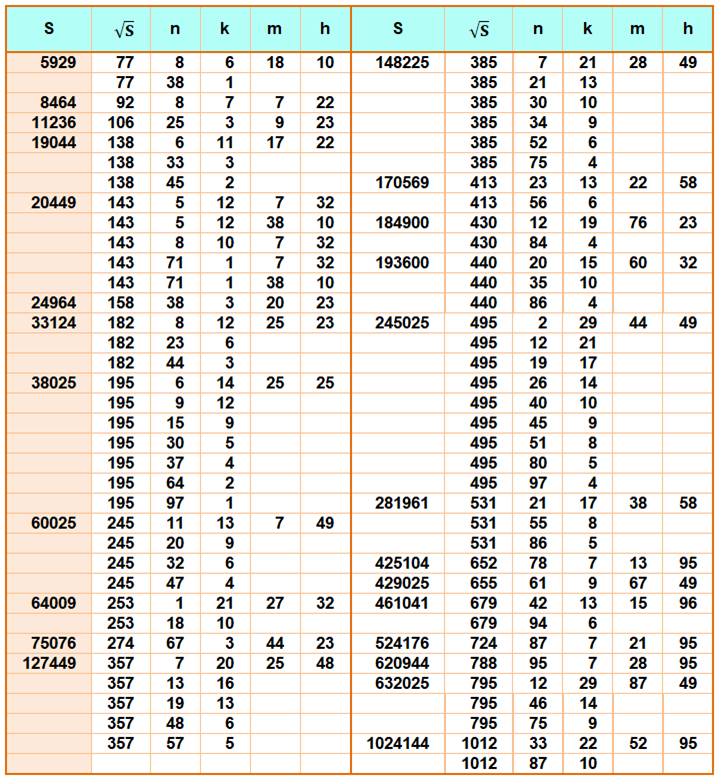
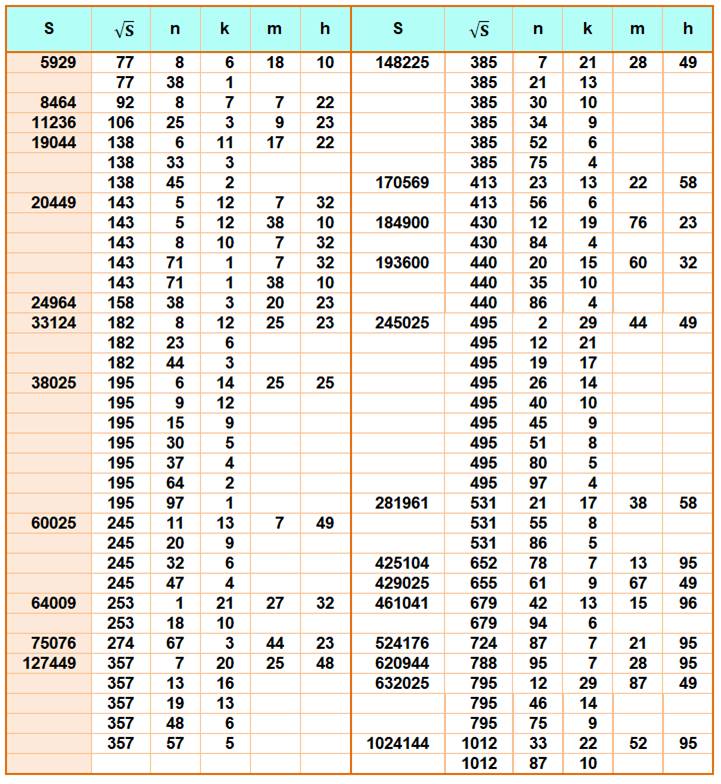
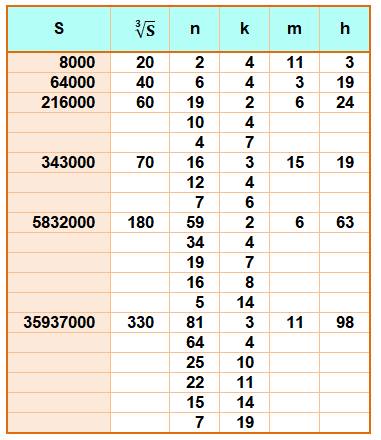
Égalité recherchée S = (n + n+1 + … + n+k)^2 = m^3 + (m+1)^3 +…+ (m+h)^3 Exemple de lecture S = 41 616 = 204^2= (4 + 5 + … + 20)^2 = (22 + 23 + … + 29)^2 = (67 + 68 + 69)^2 = 23^3 + 24^3 +25^3 Table pour n, k, m, h jusqu'à 100

DicoNombre: 204/ 312 / 315 / 323 / 504

Merci à Soufiane D.O.

Carré de somme = somme de cubes (non consécutifs)
On lâche la contrainte en cherchant des sommes avec de nombres parmi les nombres de 1 à n. Les solutions sont en nombre infini.
Exemples	9 = 3² = 1^3 + 2^3 36 = 6² = (1+5)² = (2+4)² = (1+2+3)² = 1^3 + 2^3 + 3^3 64 = 8² = (1+7)² = (2+6)² = (3+5)² = (1+2+5)² = (1+3+4)² = 4^3
Explications	Cas général: somme des cubes consécutifs = carré Pour toutes les sommes S des cubes de 1 à n consécutifs, on aura un carré n² de la somme des mêmes nombres (propriétés vue ci-dessus, notée en rouge)). Toutes les partitions de n avec nombres distincts sont également éligibles (notées en bleu) Cas particulier: somme de nombres au cube = carré Il existe des cas de nombres carrés avec un cube (comme 4) ou une somme de cubes (comme 1^3 + 2^3 + 4^3 + 6^3 = 289 = 17²). Toutes les partitions de la racine carrée avec nombres distincts sont éligibles. Exemple pour 289 = 17² 17² = (7+10)² = (8+9)² = (1+6+10)² = (1+7+9)² = (2+5+10)² = (2+6+9)² ) = (2+7+8)² = (3+4+10)² = (3+5+9)² = 3+6+8)² = (4+5+8)² = (4+6+7)² = 1^3+ 2^3 + 4^3 + 6^3
Table En jaune les cas réguliers de sommes de cubes consécutifs (= un carré) Les autres, cas où une somme de cubes non-consécutif est égale à un carré. Exemples de lecture 1^3 + 2^3 = 9 = 3² 4^3 + 8^3 = 576 = 24² Rappel Toutes les partitions en nombres distincts (ou non) de la racine carrée conduit à l'égalité: carré de somme = somme des cubes.

Voir Carrés = somme de cubes

Autres recherches

Cube de somme de consécutifs = somme de carrés consécutifs
Égalité recherchée S = (n + n+1 + … + n+k)^3 = m^2 + (m+1)^2 +…+ (m+h)^2 Exemple de lecture S = 103 823 = 47^3 = (23 + 24)^3 = 22^2 + 23^2 + … + 68^2 Table pour n, k, m, h jusqu'à 100

DicoNombre: 47 / 65

Carré de somme de consécutifs = somme de carrés consécutifs
Égalité recherchée S = (n + n+1 + … + n+k)^2 = m^2 + (m+1)^2 +…+ (m+h)^2 Exemple de lecture S = 5 929 = 77^2 = (8 + 9 + … + 14)^3 = 18^2 + 19^2 + … + 28^2 Table pour n, k, m, h jusqu'à 100

DicoNombre: 77

Cube de somme de consécutifs = somme de cubes consécutifs
Égalité recherchée S = (n + n+1 + … + n+k)^3 = m^3 + (m+1)^3 +…+ (m+h)^3 Exemple de lecture S = 8 0000 = 20^3 = (2 + 3 + … + 6)^3 = 11^3 + 12^3 + 13^3 + 14^3 Table pour n, k, m, h jusqu'à 100

DicoNombre: 20

Retour	Somme de puissances Somme de quatre cubes Carrés = somme de cubes – Partitions
Suite	Somme cubes = carré – démo Sommes des cubes des impairs Somme de cubes n fois Nombres narcissiques cubes S'y retrouver dans les sommes de puissances
Tables	Carrés, cubes … et leurs cumuls Tables – Index
Voir	Années Pythagore Carrés sommes de cubes, en général Conjecture de Catalan  Décade de Pythagore Identités Nombres carrés Nombres consécutifs Nombres cubes Nombres triangles Partition & Addition Raisonnement par récurrence Somme des entiers, carrés, cubes … Théorie des nombres Triplets de Pythagore Unité des puissances
Sites	Somme ces n premiers cubes – Wikipédia Sum of Cubes is Square of Sum - Edward Barbeau, Samer Seraj – 2013 Al-Karaji: Calcul de polynômes – Wikipédia Sums of Powers of Positive Integers –Janet Beery
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/CarSCube.htm