NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/03/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	PUISSANCES
Débutants Nombres géométriques	CARRÉS et PUISSANCES					Glossaire Nombres géométriques
INDEX Puissances	Carrés	Formes		Derniers chiffres	Terminaison
			Sommaire de cette page >>> Approche >>> Tables des puissances et unités >>> Pour chaque puissance >>> Répétition des motifs >>> Carrés et leurs dizaines >>> Recherche des derniers chiffres d'une puissance >>> Programmation – Derniers chiffres des puissances

Derniers chiffres des

PUISSANCES

Calculons la puissance d'un nombre. Observons le chiffre des unités. Qui ne sera pas émerveillé par leur régularité? Un cycle continu des mêmes chiffres dont la somme est également très stable.

Guide sur cette page: deux manières de considérer les derniers chiffres des puissances:

examen d'une puissance pour tous les nombres >>>

examen d'un nombre à toutes les puissances >>>

avec comme exemple les puissances de 2 >>>

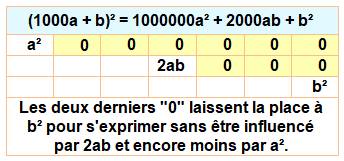
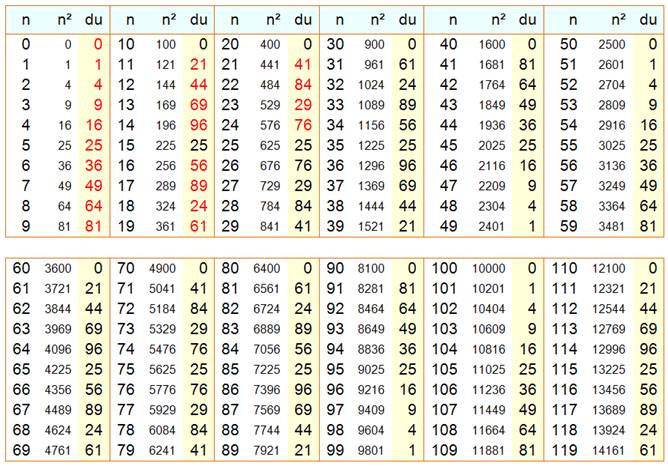
Reconnaitre un carré d'un coup d'œil

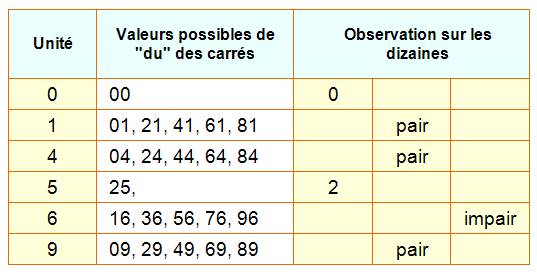
Caractérisation L'unité d'un carré n'est jamais 2, 3, 7 ou 8. Les carrés se terminent par ces deux derniers chiffres uniquement. Explication

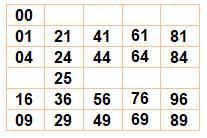
Deux derniers chiffres des carrés

Voir Factorisation de Fermat

Exploration par puissances

APPROCHE
Il est amusant d'observer le dernier chiffre des puissances des nombres. Le dernier chiffre du carré de 6, par exemple, est le 6 de 36. Dans ce cas le carré conserve le chiffre de ses unités. C'est le cas pour tous les nombres en 1, en 5 ou en 6; et bien entendu en 0. Mais ce n'est pas tout …

L'aviez-vous remarqué?

Toutes les puissances de 5 se terminent par 5.

Toutes les puissances de 6 se terminent par 6.

TABLES des puissances et de leurs unités

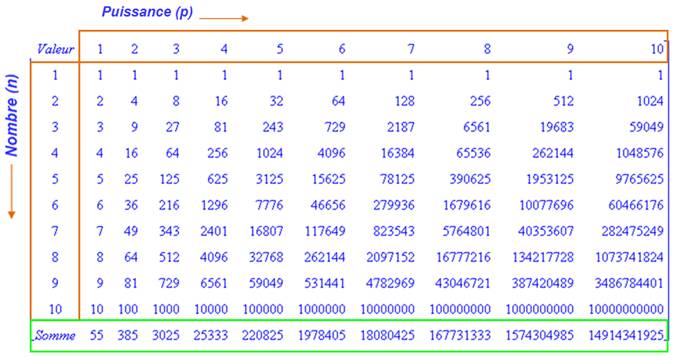
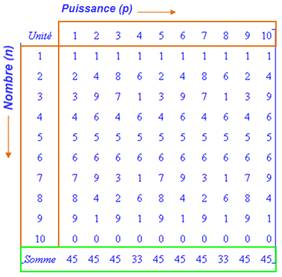
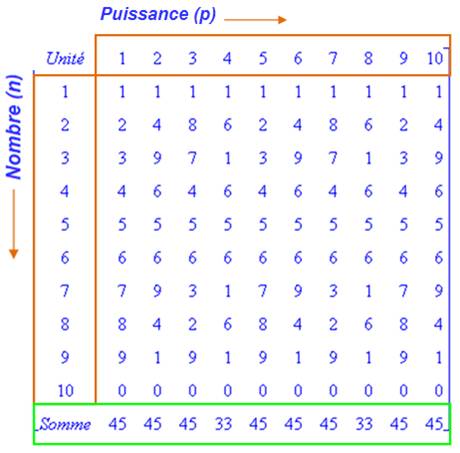
Valeurs des puissances de 1 à 10 des nombres des nombres de 1 à 10 Voir Calcul de la somme des puissances de nombres consécutifs Exemple de lecture 2^5 = 32; 3^5 = 243; 9^2 = 81; 9^3 = 729; Report de leurs unités Le même tableau, mais en ne conservant que le chiffre des unités Observations verticales La séquence 1, 2, 3 … se trouve en colonne de la puissance 1, c'est normal; et aussi en colonne de la puissance 9. Les colonnes des puissances 2, 6 et 10 présentent le même motif: 1, 4, 9, 6, 5, 6, 9, 4, 1, 0. Notez l'allure symétrique (palindromique) de ce motif. Notez en pied de colonne la somme des chiffres des unités: 45 ou 33. Observations horizontales Les chiffres sur une ligne se répètent. Ce qui veut dire que tous les nombres se terminant par 2, par exemple, ont une puissance qui se termine par 2, 4, 8 ou 6, dans cet ordre. Suite >>>

Pour chaque puissance de 1 à 5

Nombres

Unités

0

1

2

3

4

5

6

7

8

9

Somme constante des termes symétriques:

0 + 9 = 1 + 8 = 2 + 7 = … = 9

Somme totale: 45

Carrés

Unités

0

1

4

9

6

5

6

9

4

1

Que les six chiffres: 0, 1, 4, 5, 6, 9.

Symétrie par rapport à 5 (hors le 0).
Lecture palindrome: de gauche à droite comme de droite à gauche

Somme totale: 45.

Dizaines

00, 01, 04, 09, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89, 96.

Tous les carrés se terminent par l'un de ces vingt-deux nombres à deux chiffres >>>

Un carré ne se termine jamais par deux chiffres identiques, sauf pour 0 et 4 (comme 144 = 12²). A fortiori, les seuls trois chiffres répétés possibles sont 0 et 4 (comme 213 444 = 462²).

Un carré terminé par 5, l'est par 25.

Un carré terminé par un chiffre impair, la dizaine est paire.

Un carré terminé par un chiffre pair, la dizaine est impaire, sauf pour 4.

Un carré terminé par 4, alors la dizaine est paire.

Tout carré n² ou n² – 1 est divisible par 3. >>>

Tout carré n² ou n² – 1 est divisible par 4.

Tout carré n² ou n² – 1 ou n² + 1 est divisible par 5.

Cubes

Unités

0

1

8

7

4

5

6

3

2

9

Tous les chiffres possibles

Somme constante des termes symétriques (hors le 0):
1 + 9 = 8 + 2 = 7 + 3 = … = 10

Somme totale: 45.

Voir Unités des cubes

Bicarrés (puissance 4)

Unités

0

1

6

1

6

5

6

1

6

1

Symétrie par rapport à 5 (hors le 0).

Somme totale: 33 valable pour toutes les puissances en 4k.

Outre l'observation, on le démontre facilement.

D'abord la symétrie de (-n)⁴ n⁴

Il suffit de calculer d'examiner les quelques cas suivants:

0⁴ = 0, 1⁴ = 1, 2⁴ = 16, 3⁴ = 81, 4⁴ = 256 et 5⁴ = 625.

Puissance 5

Unités

0

1

2

3

4

5

6

7

8

9

Comme les unités

Somme totale: 45.

Théorèmes

N et N⁵ ont la même unité.

N et N⁹ ont la même unité.

Voir Derniers chiffres des puissances / Brève 859

Répétition des motifs
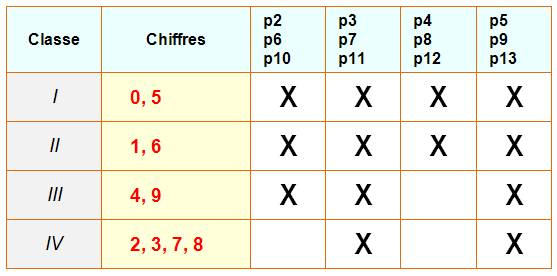
Colonne de motifs identiques pour: 1, 5, 9 … 1 + 4k 2, 6, 10 … 2 + 4k 3, 7 … 3 + 4k 4, 8 … 4 + 4k Classes des chiffres selon leur unité. Tableau montrant la présence des chiffres selon la puissance: En ajoutant un chiffre de la classe I à n'importe lequel des chiffres d'une autre classe, on retombe dans la même classe: Exemples: 5 + 4 = 9 (classe III); 8 + 5 = 13 => 3 (classe IV).

Carrés et leurs dizaines

Ce tableau montre les nombres de 0 à 119, leur carré et, une colonne spéciale en jaune donnant les dizaines et les unités (du). En rouge, les nombres du qui apparaissent pour la première fois. Il y en a 22. On observe aussi que ces colonnes se répètent cinq colonnes plus loin. Par exemple, les colonnes: 0, 5, 10, 15 … sont identiques; de même pour 1, 6, 11, 16 … Propriétés complémentaire Rangeons les vingt-deux nombres selon leur unité et observons le chiffre des dizaines:

Voir Carré magique carré 3 x 3 / Développement sur ce thème

Derniers chiffres des puissances de 2 – Comme exemple de calculs

Unité des puissances de 2
Principe de la recherche Le but est de trouver l'unité d'une grande puissance de 2 sans faire le calcul. Plusieurs méthodes possibles. La dernière présentée est la plus rapide; les autres sont présentées car susceptibles d'applications plus générales. On utilise l'arithmétique modulaire qui s'intéresse uniquement aux restes des divisions. Pour trouver l'unité d'un nombre, il suffit de calculer son reste lors d'une division par 10. On dit mod 10. La technique consiste ensuite à fonctionner en éliminant progressivement de la puissance. Si un nombre A a un reste R pour une certaine division, on aura le même reste pour A^k, et réciproquement. Conclusion: si nous rencontrons A^k, on peut lui substituer A dans le même monde de division par 10, par exemple. On va commencer avec 2^5 = 32 dont le reste de la division par 10 est 2. La puissance 403 de ce nombre aura aussi un reste égal à 2 dans la division par 10. Le nombre 2^5 est remplacé 2. Calculs avec l'arithmétique modulaire
Calcul 1 Avec 2^5 = 32 => 2 mod 10
Calcul 2 Avec 2^9 = 512 => 2 mod 10
Calcul 3 Avec 2^4 = 16 => 6 mod 10 et …6^k => 6 mod 10
Calcul des deux derniers chiffres Avec 2^22 = 4 194 304 => 4 mod 100

Voir Puissances de 2 – Propriétés

Méthode par conversion binaire
La puissance est évaluée en termes de puissances de 2, celles utilisées dans la conversion binaire.
Conversion binaire pour le dernier chiffre	201810 = 11 111 100 0102 Table des puissances de 2 en mod 10 …
Pour les deux derniers chiffres	Table des puissances de 2 en mod 100

Méthode des cycles
Ce dernier calcul est le plus immédiat. Voir le cycle des derniers chiffres des puissances de 2.
Pour le dernier chiffre Cycle de période 4: 2, 4, 8, 6	2018 = 4 x 504 + 2 => rang 2 => unité 4

Recherche des derniers chiffres des puissances d'un nombre quelconque

(Voir la référence: Brilliant.org)

Outils
Quels sont les derniers chiffres des puissances d'un nombre donné? Outils utilisés =>	Arithmétique modulaire >>> Théorème des restes chinois >>> Théorème d'Euler >>>

Unités des puissances – Bilan
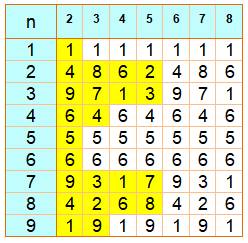
Motifs des unités des puissances Nous avons qu'un nombre terminé par 5 se terminera toujours par 5 lorsqu'il est élevé à une puissance 5^2 = 25; 15^3 = 3 375; 25^4 = 390 625 Tableau Ce tableau montre l'unité des puissances de 2 à 8 pour tous les nombres se terminant par l'unité de 1 à 9. En jaune, les seules possibilités pour chacun des chiffres. Ensuite ces chiffres se répètent. Le tableau se prolonge à droite sans fin pour toutes les puissances. La longueur de la séquence est appelée la période. Longueur de la période (Lp) Lp = 1 pour les chiffres 0, 1, 5 et 6; Lp = 2 pour les chiffres 4 et 9; et Lp = 4 pour les chiffres 2, 3, 7 et 8.		Unité des puissances 2 à 8 des nombres 1 à 9 Exemples: l'unité de 13^5 = 3 l'unité de 53^6 = 9 l'unité de 123456^789 = 6 Remarquez qu'un nombre élevé à une puissance conserve sa parité.
Exemples Unité de 19^9	19 se termine par 9 => u = {1, 9} 9 est impair => u = 9 En effet: 19^9 = 322 687 697 779
Unité de 123^456	123 se termine par3 => u = {9, 7,1, 3} 456 mod 4 = 0 => u = 1 En effet: 123^456 = 992…561 = 9,9 10^952
On retrouve bien ces unités pour les puissances de 2.	2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048 …

Arithmétique modulaire
Voir arithmétique modulaire. Quelle est l'unité de 17^17 ? On calcule quelques valeurs pour atteindre 17 = 4 x 4 + 1	u 17^17 mod 10 17^2 7^2 = 9 mod 10 17^4 9^2 = 1 mod 10 (17^4)^4 1^4 = 1 mod 10 17^17 = 17 x (17^4)^4 7 x 1 7 mod 10 En effet: 17^17 = 827 240 261 886 336 764 177
Quelle est l'unité de 2^35 ?	u 2^35 mod 10 35 = 16 + 16 + 3 2^16 (2^4)^4 6^4 6 mod 10 2^32 6 x 6 6 mod 10 2^35 8 x 6 8 mod 10 En effet: 2^35 = 34 359 738 368

Théorème des restes chinois
L'idée avec les restes chinois consiste à identifier un nombre mod 2^n et un nombre 5^n et à combiner les résultats en utilisant le théorème des restes chinois pour trouver un nombre mod 10.
Quels sont les deux derniers chiffres de 74^540 ? En remarquant que 100 = 4 x 25, deux nombres premiers entre eux On calcule, non pas en mod 10, mais en mod 4 et en mod 25	74^540 2^540 x 37^540 2^4x135 x 37^4x135 0 mod 4 74^540 (75 – 1)^540 (– 1)^540 1 mod 25 Il faut trouver un nombre n tel que mod 4, il vaut 0 et mod 25, il vaut 1. Réponse n = {1, 26, 51, 76} Le seul divisible par 4 est n = 76

Théorème d'Euler
Le théorème d'Euler => Alors, un exposant b peut être réduit modulo Phi(n) sans changer la valeur de a^b mod n	Si a et n sont premiers entre eux Phi(n) est le totient d'Euler qui compte la quantité de nombres inférieurs à n et premiers avec n.
Quels sont les deux derniers chiffres de 33^42 ?	On passe par 42 = 40 + 2 Si on sait que Phi(100) = 40 Et que 33^40 1 mod 100 On déduit immédiatement que: 33^42 33^2 mod 100 1089 89 mod 100

Programmation – Derniers chiffres des puissances
	But (m, n, k) m derniers chiffres de n^i pour i de 1 à k Commentaires La procédure s'appelle FP (Fin de Puissance). La liste L est préparée pour accueillir les nombres "fin de puissance" La boucle en i tourne k fois (quantité de nombres demandée). Pd est la valeur de la puissance du nombre n à la puissance i en cours, tronquée pour ne conserver que les m derniers chiffres. C'est l'effet du modulo 10^m. À chaque itération, la valeur de fin de puissance est conservée dans la liste L. En fin de boucle, la liste L est retournée. Le programme principal demande, par exemple, les 2 derniers chiffres des puissances de 2 pour 22 puissances successives. En bleu, le résultat du traitement. On y retrouve la période de longueur 20 commençant à 4.
Programme à copier-coller dans Maple FP := proc (m, n, k) local L, i, Pd; L := []; for i to k do Pd := `mod`(n^i, 10^m); L := [op(L), Pd] end do; return L end proc; FP(2, 2, 22);

Voir Programmation – Index / Tables des puissances de 2 et leurs derniers chiffres

Suite	Terminaison des carrés Les nombres carrés Système décimal – Unités Terminaisons des produits Cycle des chiffres des carrés Puissance 1001 Divisibilité de différence de puissances d'un nombre Puissances terminées par 00…01 Nombres et les chiffres de leurs puissances Unités des produits
Voir	Carrés – Calcul mental Carrés – Somme pour nombres successifs Carrés somme de cubes Chemin d'Euler Chiffres dans leurs puissances Cubes – Calcul mental Cubes – Modulo Cubes – Somme pour nombres successifs Dualité Exponentielle Nombres automorphiques Nombres géométriques Partition & Addition Permutation des chiffres et puissances Racine carrée Racines - Calcul
Diconombre	Nombre 2
Site	Finding the Last Digit of a Power – Brilliant.org.
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/UnitPuis.htm