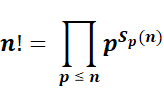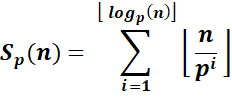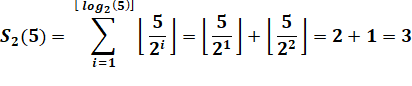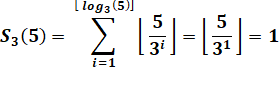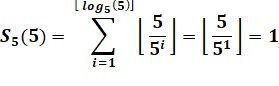|
||||||||||||||||||||||||||||
![]()
|
FACTORIELLES – Propriété Factorielle jamais carrée Sauf 1!, les factorielles ne
sont jamais un carré. Ni d'ailleurs les factorielles
tronquées. Exemple de démonstration
s'appuyant sur l'observation. Puis démonstration selon une
poursuite sans fin de la factorielle carrée. |
Théorème d'Erdös et Selfridge (1975)
|
Le produit de
nombres consécutifs n'est jamais une puissance. The product of
consecutive integers is never a power. |
|
|
||
|
La
factorisation d'un nombre carré comporte des facteurs
premiers au moins au carré ou puissance 4, ou puissance 2k. |
9 =
32 16 = 24 36 = 22 x 32 180 = 22 x 32 x 5 n'est pas un carré (le facteur premier 5 est seul) |
|
|
Pour être
un carré, le facteur premier le plus grand du nombre doit être répété. |
180 x 5
= 22 x 32 x 5 x 5
est un carré 180 x 5 = 900 = 302 |
|
|
Le théorème de Tchebychev dit que,
au moins un nombre premier se glisse entre n et 2n. |
Entre 7 et 14, on trouve les nombres
premiers: 11 et 13 |
|
|
|
||
|
Le tableau des nombres factoriels et de leurs facteurs premiers |
Démonstration en trois temps |
|
|
|
||
|
|
|||
|
Propriété
des factorielles |
Le dernier nombre premier
à diviser n! est inférieur à n. |
8! = 40 320 = 27
x 32 x 5 x 7 et 7
< 8 |
|
|
Principe de la démonstration |
Soit un nombre de départ. On montre qu'il
faudrait qu'il soit plus grand pour que sa factorielle soit un carré. Or
c'est impossible, car il faudrait qu'il soit encore plus grand, etc. C'est le théorème de Tchebychev qui joue le
trouble-fête en introduisant un nombre premier qui relance la poursuite sans
fin. |
||
|
1) Si n est premier |
n! = 1x2x …x p |
5! = 23 x 3 x 5 = 120 |
|
|
Pour
former un carré le facteur p doit être doublé. |
Or, tous les autres facteurs sont
inférieurs à p. Impossible de doubler p. |
Pas d'autre 5 dans la factorisation de 120. 120 ne peut pas être un carré. |
|
|
2) Si n est composé, le plus grand premier inférieur à n est p |
n = Ap p < n |
8! = 40 320 = 27
x 32 x 5 x 7 p = 7 |
|
|
Pour
former un carré le facteur p doit être répété (seul ou multiples). |
La seule chance est que n soit supérieur ou
égal à 2p n |
Pour faire un carré, il faut au moins un
autre 7. Ce sera le cas pour 14 > 8 |
|
|
Or selon
le théorème de Tchebychev un autre premier p' est là |
p' < 2p |
Avant d'atteindre 14, les premiers 11 et 13
font leur apparition. |
|
|
La
présence de p' impose que lui aussi soit doublé pour former un carré |
de n! à 2p! il n'y a pas de carré |
De 8! à 14! il n'y a pas de carré |
|
|
En repartant
de n = p', on recommence la démonstration depuis le début |
p'! n'est pas un carré car p' est premier Pour les nombres suivant avant d'atteindre
2p', il y aura au moins un p". Etc. |
11! n'st pas premier il faudrait atteindre (2x11)! mais, entre-temps
s'autre premiers vont apparaitre (13, 19 et 27). |
|
|
|
|||
|
Formule de Polignac Pour un
entier n > 0, la décomposition en
facteurs premiers de n! est donnée par cette formule. Sorte de
décomposition p-adique |
|
||
|
Exemple 5! = 120
= 23 x 3 x 5 Alors p =
{2, 3, 5} |
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()