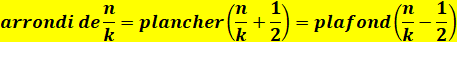|
||||||||||||||||||||||||||||||
![]()
Humour
|
Un
élève en classe: je comprends plus, monsieur, vous nous avez appris comment
mettre les nombres au carré et maintenant
vous nous demandez de les arrondir … |
Voir Pensées et Humour
|
Nombres
RONDS
& Nombres ARRONDIS Le nombre rond est une
notion utilisée surtout en calcul mental
ou pour délivrer une approximation. L'arrondi d'un nombre est
une valeur approchée de ce nombre avec moins de chiffres. On perd volontairement de la précision au profit
d'une manipulation ou d'une mémorisation plus facile. Quels sont les types
d'arrondis? Leurs résultats? Comment arrondir de la même manière des nombres
très différents? Comment fixer la quantité de chiffres significatifs? Voir l'astuce des nombres négatifs ou celle des logarithmes. |
|
|
|
|
Un nombre rond n'a pas
de définition précise. Tout dépend du contexte.
|
|
|
École primaire |
|
|
On y apprend que le nombre rond se
termine par, au moins, un zéro. |
20, 1200, 53 000
... |
|
Il est utile de les repérer et de
les maîtriser, car la présence de zéros facilite le calcul mental. |
13 + 17 = 30 L'addition des unités donne un nombre rond (10) |
|
Additions |
4 + 6
+ 7 = (4 + 6) + 7 =
10 + 7 =
17 |
|
|
12 + 25 + 8 + 15
+ 9 = (12 + 8) + (25 + 15) + 9 =
20 + 40
+ 9 = 69 |
|
Soustractions |
57 – 7 = 50 |
|
|
60 – 7 = 53 |
|
|
53 –
8 = 53 – 10 + 2 = 43 + 2 = 45 |
|
Multiplications |
5 x 10 = 50 |
|
|
12 x 10 = 120 |
|
Multiplications |
12 x 13 = =
10 x 13 + 2 x 13 = 130
+ 26 = 156 |
|
Nombres à virgule |
1,5
+ 2,3 + 7,5 = (1,5 + 7,5) + 2,3 =
9 + 2,3 =
11,3 |
Voir Enseignement
|
Sens général |
|
|
Au sens
d'arrondi |
Au sens
approximatif |
|
Chiffre,
nombre, compte rond:
nombre entier ou ramené à un
nombre entier, ne comprenant pas de décimales. Sans
fraction. Arrondi à la dizaine, la centaine, le
millier … |
Utilisé pour
donner un ordre
de grandeur simple à visualiser. Ex: En chiffres ronds, ça fera 10 000
euros. Anglais: round number |
|
Tout
rond:
constat d'un fait en nombre rond (rond
prend la marque du pluriel). Ex: Nous étions cent tout ronds. Il avait
quinze ans tout ronds (avec ou sans s) Anglais: 1% tout
rond: at 1% all in; 30 mètres tout ronds: 30 meters sharp. Note: chiffre estimé, à la louche,
pifométrique: ballpark figure, rough figure. Ex: Le marketing impose des nombres
tels que 4,99 euros, évitant de donner
5 euros en chiffre rond. Orthographe: on écrit généralement les chiffres ronds en toutes lettres. |
|
Voir
Anglais et nombres / Nombres ronds en théorie des nombres
![]()
|
|
||
|
.
En effet, cette valeur de Pi est souvent largement
suffisante pour de nombreux calculs. |
||
|
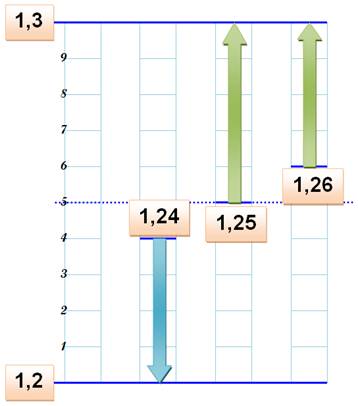
Trois exemples illustrés
1,24 1,25 1,26 |
|
|
Voir
Incertitude et précision sur un résultat de mesure
Nombre arrondi à
l'unité
|
L'arrondi à
l'unité d'un nombre décimal est le nombre entier
le plus proche de celui-ci au sens de l'arrondi. |
Exemples
3,14 => 3 3,50 => 4 3,7 => 4 |
Arrondi à l'unité:
Devinette (sorte de charade)
|
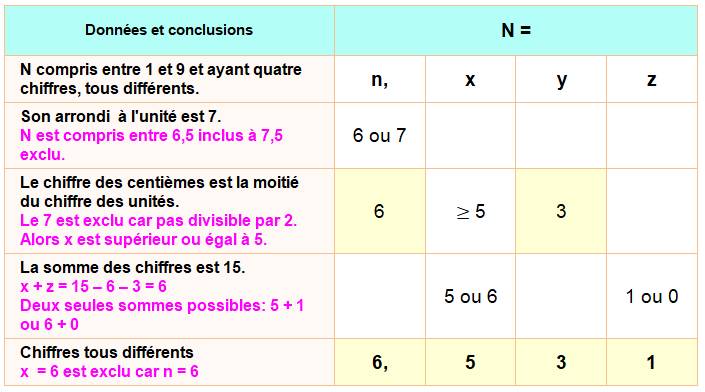
Trouvez N qui est
un nombre décimal:
|
|
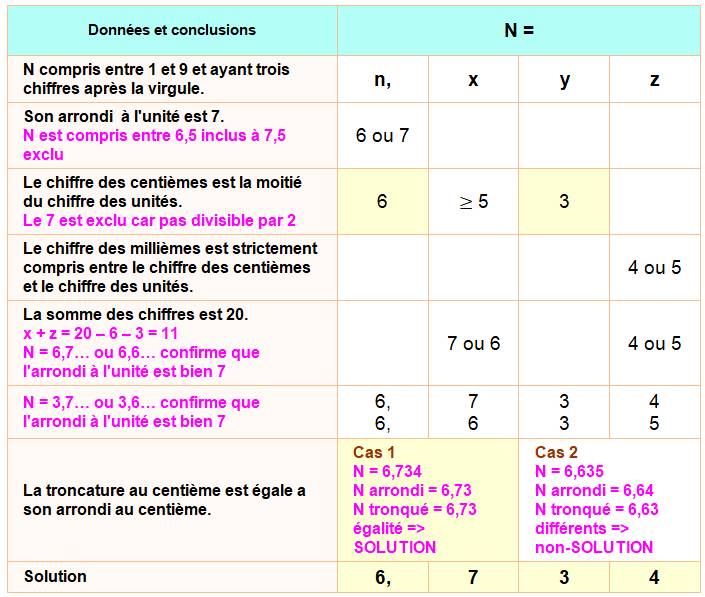
Variante Trouvez N qui est
un nombre décimal:
|
|
|
|
|
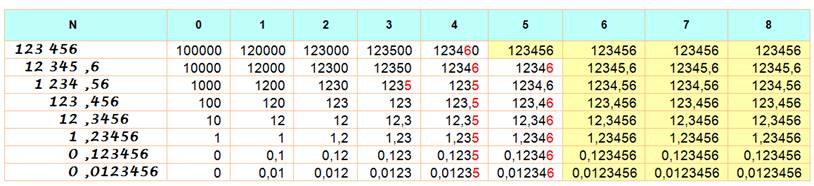
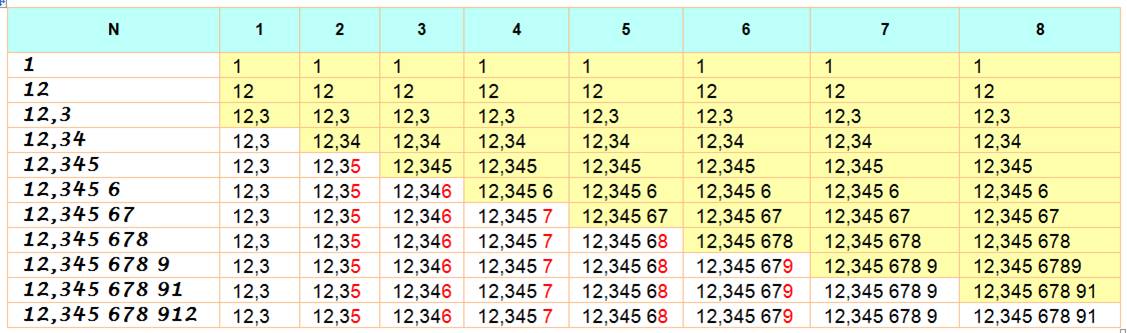
Principe
Exemples
Selon la fonction "arrondi" du tableur Excel |
|
|
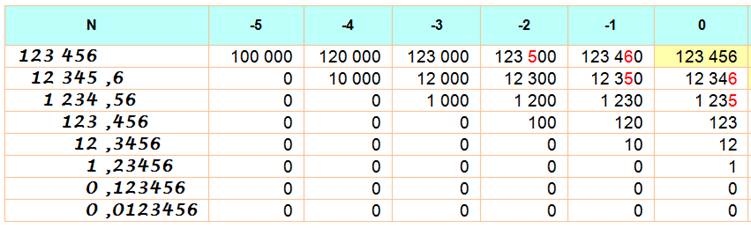
Lecture et observations selon cinq zones (voir illustration)
|
|
|
|
|
|
|
|
|
||
|
|
||
|
|
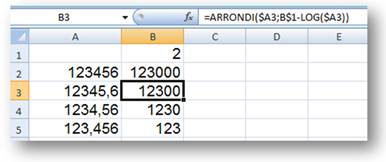
En écrivant la formule en B2 avec les $, je tire
sur la poignée en bas à droite et j'obtiens automatiquement la copie des
formules dans les lignes suivantes. |
|
|
|
|||
|
Vu ci-dessus |
=ARRONDI(G5;1) (Valeurs
entre parenthèses: indicatives) |
1,2345 |
|
|
Force l'arrondi
à la valeur inférieure |
=ARRONDI.INF(G6;2) |
1,239 |
|
|
Force l'arrondi
à la valeur supérieure |
=ARRONDI.SUP(G7;2) |
1,231 |
|
|
Arrondi à la
valeur d'un multiple du nombre indiqué. Ici, multiple de 7 |
=ARRONDI.AU.MULTIPLE(G10;7) |
15,23 |
|
|
Arrondi à
l'entier inférieur. Effet avec multiples selon le second argument. Voir votre tableur. |
=PLANCHER(G8;1) Notation: |
12,7 |
|
|
Arrondi à
l'entier supérieur. Effet avec multiples selon le second argument. Voir votre tableur. |
=PLAFOND(G9;1) Notation: |
12,7 |
|
|
Supprime
toutes les décimales. |
=ENT(G11) |
123,456 |
|
|
Supprime les
décimales au-delà d'une certaine quantité. Ici, 3. |
=TRONQUE(G12;3) |
1,2345 |
|
|
Retourne le
nombre sans son signe |
=ABS(G13) |
-123,4 |
|
Troncature à l'unité
|
La troncature
à l'unité d'un nombre décimal est le nombre
entier sans sa partie décimale |
Exemples
3,14 => 3 3,50 => 3 3,7 => 3 |
Bon à savoir pour un
résultat en nombres entiers
|
Exemple: 10/3 = 3,333…
|
Voir Brève
739
|
|
|||
|
|
evalf (Pi,15) |
3.14159265358979 |
|
|
|
length(123456789) |
9 |
|
|
|
round(123,456) round(123,56) round(123,6) |
123 124 124 |
|
|
|
trunc(123,456) trunc(-123,456) |
123 -123 |
|
|
|
frac(123,456) frac(-123,456) |
0.456 -0.456 |
|
|
|
floor |
|
|
|
|
ceil |
|
|
|
Un tableur offre
de multiples possibilités pour obtenir une valeur approchée d'un nombre.
L'arrondi arithmétique est la plus courante. Avec un nombre négatif, on
précise le nombre de chiffre significatif même avant la virgule. Avec recours
aux logarithmes, on fixe le nombre de chiffres significatifs. Les fonctions
comme entier et tronque sont utiles pour isoler des
chiffres dans un nombre. |
|
Decimal place (d.p.): digits after the decimal point. 27,7 (1 d.p.) signifie que le calcul est donné
(est exact) pour une décimale après la virgule, ce qui veut dire que le
nombre a été arrondi. Ex: write
2.6470588 to 2 decimal places (dp). Answer: 2,65. Significant figure: même règle, mais en
donnant la quantité totale de chiffres. Ex: 2.6470588 to 3 significant
figures (sf). Answer: 2,65. |
![]()
Variante
Retour / Cryptarithmes
/ Énigmes
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
![]()