|
||||||||||||
![]()
|
|
|
|
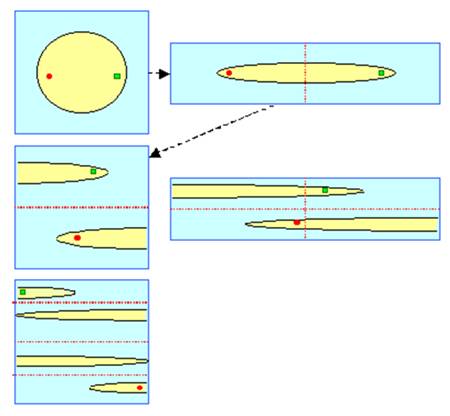
Pâte
feuilletée:
Illustration:
Dans
cet exemple,
Généralisation:
|
|
|
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
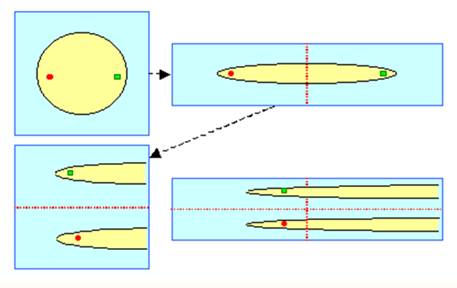
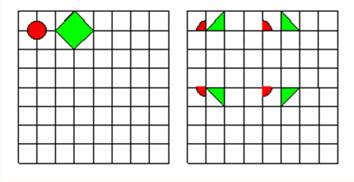
Exemple avec la pomme: ERGODICITÉ
|
En itérant un grand
nombre de fois la transformation du boulanger, on observe que les points
d’une partie A donnée au départ semblent se répartir uniformément dans tout
le carré :
Cette propriété porte
le nom de mélange. La transformation du
boulanger est souvent citée comme un exemple permettant de comprendre ce
qu'est la théorie
ergodique. En effet, et en gros,
la théorie ergodique c'est cela: vous avez
un espace et une transformation que vous appliquez sans cesse. La question
est de savoir si l'espace va devenir en quelque sorte homogène selon une définition
à préciser. |
Source image: Théorie
ergodique – Introduction et premiers exemples – T. de la Rue
|
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
![]()