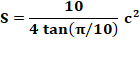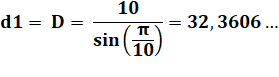Décagone

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/07/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Polygones
Débutants Géométrie	POLYGONES un par un									Glossaire Géométrie
INDEX Polygones Géométrie	Noms	-1-	-2-	-3-	-4-	-5-	-6-	-7-	-8-		-9-
	10	11	12	13	14	15	16	17	18		19
	20			23
	Sommaire de cette page >>> Quelques décagones >>> Décagone régulier >>> Calcul sur un angle >>> Nombre d'or >>> Apothème >>> Distance des côtés à un point quelconque >>> Relations a, p , r >>> Décagone et triangles équilatéraux >>> Fleurs >>> Dodécagone régulier et ses diagonales >>> Exercice de calcul des longueurs

DÉCAGONE

Polygone à 10 côtés.

Du grec deka: dix et gônia: angle. Figure plane à dix angles et dix côtés.

Quelques DÉCAGONES

Décagone régulier – Angles et aire

Aire du dodécagone avec a la mesure de son côté:

= 7,6942088429381335065… a²

= 2,5 d.a = 5 p.a

avec d distance entre deux côtés parallèles

et p l'apothème.

En effet: aire du triangle bleu = ½ p.a;

à multiplier par 10 pour le décagone complet.

Présence de l'angle de 36° = Pi/5

Notez les angles dessinés en bleu

Voir Angle 36° / Nombre 36

Calcul sur un angle
Question Donnez la valeur de l'angle HJD. Réponse 1) Un polygone régulier s'inscrit dans un cercle (cercle qui passe par les dix sommets). Le point O est son centre. Les rayons (OA, OB …) joignant chacun des dix sommets forment dix angles (AOB, BOC ...). La somme de ces angles vaut 360°. Chacun de ces angles au centre intercepte des cordes égales (les cotés du décagone), ces angles sont égaux. Chacun mesure: 360 / 10 = 36° au choix: sont égaux, sont isométriques, ont la même mesure.
2) Le triangle AOJ, ayant deux côtés égaux (OA et OJ qui sont des rayons du cercle) est isocèle: angle JAO = angle AJO. Or, la somme des angles dans un triangle est 180°: Angle AOJ + 2 x angle AJO = 180° Angle AOJ vaut 36° (vu au 1)): Angle AJO = (180 – 36) / 2 = 72° Un angle du dodécagone tel que AJI = AJO + IJO vaut deux fois cette valeur: 144° 3) Nous devons calculer la mesure de l'angle HJD, de sommet J. De ce sommet sont issus huit angles égaux, car ils interceptent tous la même corde. Chacun mesure 144 / 8 = 18°. L'angle HJD englobe quatre de ces angles: Angle HJD = 4 x 18 = 72° Alternative L'angle au centre HOD = 4 x 36 = 144°. L'angle inscrit qui intercepte le même arc (HD) vaut la moitié: 144 / 2 = 72°. Remarque En prenant l'angle IJD qui englobe cinq angles élémentaires, nous trouvons 5 x 18 = 90°. Nous retrouvons, la propriété classique: un angle inscrit qui intercepte un diamètre est un angle droit.

Nombre d'or

Le nombre d'or se retrouve dans le décagone comme dans le pentagone.

OA: rayon du cercle circonscrit.

AB: côté du décagone régulier convexe.

AD: côté du décagone étoilé.

FD: coté du pentagone régulier convexe.

FB: côté du pentagone étoilé

Démonstration

Rayons OA et OB sont égaux	Triangle 0AB isocèle
Angle au sommet 0 = 36° (1)	Angles en A et B = 72° (2)
Arcs BD et DF égaux	Angles BAD et DAF égaux (1) AD bissectrice de OAB
Angles AOB et OAM égaux à 36° (1)	Triangle AMO isocèle MA = MO
Triangle ABM: somme des angles = 180°	Angle MAB (36°) et ABM (72°) => angle BMA = 72° (type 2)
Angles égaux AMB et MBA	Triangle ABM isocèle => AB = AM = MO
Bissectrice AD et son théorème
En ramenant tout sur OB, compte tenu des égalités trouvées
Division en moyenne et extrême raison, définition du nombre d'or.
Cas du pentagone de côté BD	BD = DF BDF isocèle Angle 36° (type (1)
Triangles BDF et AMO	Semblables
Rapport

Apothèmes
Décagone, occasion de montrer les propriétés de l'apothème.
Angle ABF et angle ADF interceptent un diamètre	Ce sont des angles droits
Apothème OH du décagone	Angle droit en H OH et FB sont parallèles
Triangle ABF et Thales
Conclusion	OH = ½ FB
Même démo.	OL = ½ FD
	OM = ½ AD

Voir Bases de géométrie

Distance des côtés à un point quelconque Longueur de l'apothème		haut
Problème Quelle est la longueur totale des distances D de type PH dans ce décagone ? Solution L'aire des triangles de type PAB vaut ½ AB·PH La somme des aires de tous ces triangles vaut: C'est aussi l'aire du décagone: En rapprochant les deux valeurs:
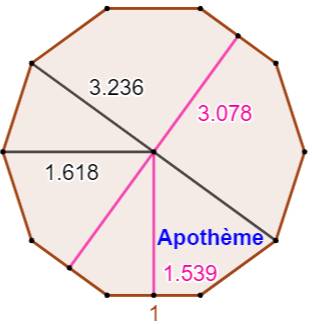
Apothème Avec le point P au centre du décagone (centre du cercle circonscrit, la somme des distances vaut dix fois l'apothème p. Le rayon est égal au nombre d'or: 1, 618… Rappel Voir Table

Voir Apothème du pentagone

Tableau des relations

Entre a le côté, r le rayon du cercle circonscrit et p l'apothème

Voir Nombre d'or et trigonométrie / Angles du pentagone et trigo

Décagone et triangles équilatéraux / pentagones

Notez les points d'intersection selon la taille des triangles équilatéraux (figure de gauche, matérialisés par le rectangle) et, selon celle des pentagones réguliers (figure de droite).

Fleurs

Certaines fleurs, mais c'est rare, disposent de:

dix pétales
Ici: passiflore.

cinq pétales fortement divisés

Ici: silène avec détail de la corolle.

et, sakura

Note: les rosacées (rosier et la plupart des arbres fruitiers) ont, en général, 5 pétales et 5 sépales.

Ici, la rose Belle de Crécy.

Voir Phyllotaxie

Décagone régulier et ses diagonales

Longueur de la diagonale k, avec k la quantité de côtés interceptés par la diagonale.

k	Longueur	Formule
2	1,902113033
3	2,618033989
4	3,077683538
5	3,236067977

Voir Son calcul / Tables / Quantité d'intersections des diagonales

Diagonales du décagone – Calcul des longueurs
Exercice de géométrie Angle au sommet interceptant un côté Diagonales d1 = AF = D d2 = AG = AE = BF = 2r d3 = AD d4 = AC Rayon des cercles circonscrit: MF = R = D/2 inscrit: MP = r Apothème MP = FB/2 = r Calculs des longueurs pour une longueur du côté: a = 10.
Grande diagonale d1 = AG, diamètre du cercle circonscrit (D):
Deuxième diagonale, diamètre du cercle inscrit, 2 x apothème: d2 = 2r = FB
Petite diagonale d4 = AC:
Deuxième diagonale d2 = AD:

Suite	Rosaces à dix pétales Construction du décagone Nombres décagonaux Dissection du décagone en carré Pavage de Penrose Dodécagone Icosagone Construction de l'heptagone à partir d'un décagone
Retour	Pentagone
Voir	Calcul de Pi Construction géométrique des nombres Géométrie – Index Polygone Pavage avec polygones Partage du cercle en parts égales Hexagone – Généralités
Diconombre	Nombre 7,69... Nombre 10
Livre	Le nombre d'or – Marius Cleyet-Michaud – puf - 1973
Site	Construction animée du décagone - Wikipedia
Cette page	http://villemin.gerard.free.fr/GeomLAV/Polygone/Decagone.htm