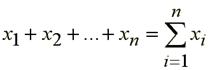|
|
Définition |
|
||||||||||||
|
|
|||||||||||||
|
Somme |
|
|
Maths |
A
et B étant deux ensembles disjoints, de cardinal a et b Tr
|
|
Construction |
|
|
Propriétés |
|
|
Somme |
|
|
Anglais |
-
He is not good at addition -
Have you checked the addition of the bill?
-
Add 12 to 25 -
He added up the column of figures (attention: figures = nombres!)
-
The number p(n) of partitions of an integer n into summands |
![]()
![]()
![]()
P
Nombre en surligné jaune et quantité de partitions
en pied de tableau.
En noir partition de base et en rose déclinaison.
|
1 |
2 1 + 1 |
3 2 + 1 1 + 1 + 1 |
4 3 + 1 2 + 2 2 + 1 + 1 1 + 1 + 1 + 1 |
5 4 + 1 3 + 2 3 + 1 + 1 2 + 2 + 1 2 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1 |
6 5 + 1 4 + 2 4 + 1 + 1 3 + 3 3 + 2 + 1 3 + 1 + 1 + 1 2 + 2 + 2 2 + 2 + 1 + 1 2 + 1 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1 + 1 |
|
1 |
2 |
3 |
5 |
7 |
11 |
|
7 6 + 1 5 + 2 5 + 1 + 1 4 + 3 4 + 2 + 1 4 + 1 + 1 + 1 3 + 3 + 1 3 + 2 + 2 3 + 2 + 1 + 1 3 + 1 + 1 + 1 + 1 2 + 2 + 2 + 1 2 + 2 + 1 + 1 + 1 2 + 1 + 1 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1 + 1 + 1 |
8 7 + 1 6 + 2 6 + 1 + 1 5 + 3 5 + 2 + 1 5 + 1 + 1 + 1 4 + 4 4 + 3 + 1 4 + 2 + 2 4 + 2 + 1 + 1 4 + 1 + 1 + 1 + 1 3 + 3 + 2 3 + 3 + 1 + 1 3 + 2 + 2 + 1 3 + 2 + 1 + 1 + 1 3 + 1 + 1 + 1 + 1 + 1 2 + 2 + 2 + 2 2 + 2 + 2 + 1 + 1 2 + 2 + 1 + 1 + 1 + 1 2 + 1 + 1 + 1 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 |
9 8 + 1 7 + 2 7 + 1 + 1 6 + 3 6 + 2 + 1 6 + 1 + 1 + 1 5 + 4 5 + 3 + 1 5 + 2 + 2 5 + 2 + 1 + 1 5 + 1 + 1 + 1 + 1 4 + 4 + 1 4 + 3 + 2 4 + 3 + 1 + 1 4 + 2 + 2 + 1 4 + 2 + 1 + 1 + 1 4 + 1 + 1 + 1 + 1 + 1 3 + 3 + 2 + 1 3 + 3 + 3 3 + 3 + 2 + 1 3 + 3 + 1 + 1 + 1 3 + 2 + 2 + 1 + 1 3 + 2 + 1 + 1 + 1 3 + 1 + 1 + 1 + 1 + 1 + 1 2 + 2 + 2 + 2 + 1 2 + 2 + 2 + 1 + 1 + 1 2 + 2 + 1 + 1 + 1 + 1 + 1 2 + 1 + 1 + 1 + 1 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
+
1 |
10 9 + 1 8 + 2 8 + 1 + 1 7 + 3 7 + 2 + 1 7 + 1 + 1 + 1 6 + 4 6 + 3 + 1 6 + 2 + 2 6 + 2 + 1 + 1 6 + 1 + 1 + 1 + 1 5 + 5 5 + 4 + 1 5 + 3 + 2 5 + 3 + 1 + 1 5 + 2 + 2 + 1 5 + 2 + 1 + 1 + 1 5 + 1 + 1 + 1 + 1 + 1 4 + 4 + 2 4 + 4 + 1 + 1 4 + 3 + 3 4 + 3 + 2 + 1 4 + 3 + 1 + 1 + 1 4 + 2 + 2 + 2 4 + 2 + 2 + 1 + 1 4 + 2 + 1 + 1 + 1 + 1 4 + 1 + 1 + 1 + 1 + 1 + 1 3 + 3 + 3 + 1 3 + 3 + 2 + 2 3 + 3 + 2 + 1 + 1 3 + 3 + 1 + 1 + 1 + 1 3 + 2 + 2 + 2 + 1 3 + 2 + 2 + 1 + 1 + 1 3 + 2 + 1 + 1 + 1 + 1 3 + 1 + 1 + 1 + 1 + 1 + 1 + 1 2 + 2 + 2 + 2 + 2 2 + 2 + 2 + 2 + 1 + 1 2 + 2 + 2 + 1 + 1 + 1 + 1 2 + 2 + 1 + 1 + 1 + 1 + 1 + 1 2 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1 + 1 + 1 +
1 + 1 + 1 |
|
15 |
22 |
30 |
42 |
Partitions – Introduction et tableaux pour
les premiers nombres
![]()