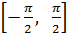|
|
Rappel: APPLICATION
Voir DicoMot
Notes -
Une
application (et une transformation) est bijective:
un point image correspond à un seul antécédent et réciproquement. -
Si
après transformation, le dessin "reste sur place", nous avons à
faire à la transformation identité. -
La
transformation qui fait revenir un dessin transformé dans sa version initiale
est l'application réciproque. -
Si
après transformation appliquée deux fois, le dessin revient à sa place,
l'application (la transformation) est involutive;
elle est sa propre réciproque. |
|
Approche |
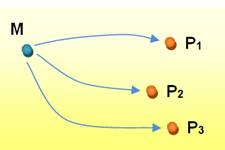
Plusieurs points P peuvent être créés à
partir d'un point M. Ce cas n'est pas intéressant! Nous intéressons effectivement aux cas où
nous transformons tous les
points M en point(s) P. |
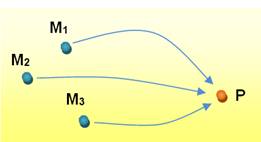
Mais une image P peut être créée à partir
de différents points M. Nous pouvons également avoir le cas où un
point P n'a pas d'antécédent M. |
![]()
Voir Bijection – Débutant
|
Cas possibles Rappel: Tout point M a au moins une
image P |
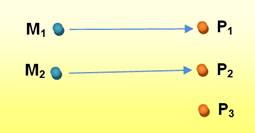
Cas où il reste des P orphelins
INJECTION Les M sont injectés dans le domaine des P, mais ne le
couvre pas forcément complètement. Si
M1 et M2 sont deux points identiques, alors leurs images sont identiques.
Si
M1 et M2 sont deux points différents, alors les deux images sont différentes.
|
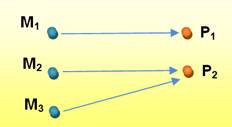
Cas où tous les P ont un ou plusieurs antécédents
SURJECTION Les M sont en surnombre pour couvrir le domaine des P. À
tout point P du domaine d'arrivée F, il existe un point M, au moins, du domaine de départ
E, tel que le point P est la transformée du point M.
|
|
L'application
|
||
|
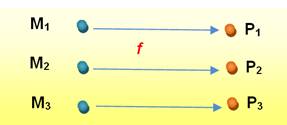
Cas où chaque P a un seul antécédent
BIJECTION = INJECTION + SURJECTION Les M sont en bon
nombre dans leur domaine pour couvrir
exactement le domaine des P. À
tout point P du domaine d'arrivée F, il existe un point M, UNIQUE, du domaine de départ
E, tel que le point P est la transformée du point M, et réciproquement:
|
||
![]()
|
Exemples |
Sont
en bijection:
Contre-exemples:
|
|
Définition |
Bijection ou transformation bijective: une transformation T de (E) dans (E) est dite
bijective, si, et seulement si, pour
tout P de (E), il existe un point M de (E) et un seul, tel que T(M) = P On aurait la même définition
pour, plus généralement, une application en donnant F comme ensemble
d'arrivée. Bijection ou fonction bijective: Soit f une application de E dans F. f
est bijective si et seulement si
qui se lit: quelque
soit y de (F), il existe un unique x de (E) tel que f(x) égal y. |
|
Propriété |
|
![]()
|
Anglais |
A bijection, or a bijective
function is a function f from
a set X to a set Y with the property that, for
every y in Y, there is exactly one x in X such that f(x) = y Alternatively, f is bijective if it is a one-to-one correspondence between
those sets; meaning that a bijection is both
one-to-one (injective) and onto (surjective). |
|
En savoir plus |
Voir suite en cliquant sur
les mots de l'en-tête
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosB/Bijectio.htm |
![]()