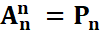|
||||||||||||||||||||||||||||||||
![]()
|
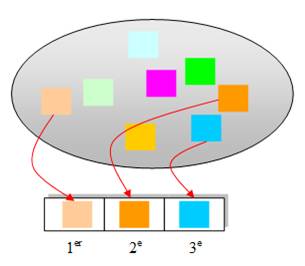
ARRANGEMENT – Introduction Sélection avec ordre et sans répétitions
|
|
|
||
|
L'ordre a son importance. Un élément choisi, ne peut plus être re-choisi. C'est un
tirage sans remise. |
|
|
|
|
||
|
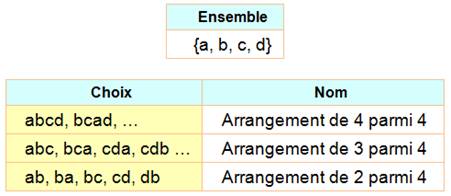
Une telle
disposition s'appelle:
|
|
|
|
Un n-arrangement est aussi appelé permutation. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Permutations Il
s'agit de donner un rang de 1 à n à chacun n objets |
Arrangements Il
s'agit de donner un rang de 1 à p à p parmi n objets |
|||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||
|
Ici est représentée
la permutation BDCA. |
Ici est représenté
l'arrangement BD. Note: On
remarque que, une fois le premier placé, il y a 3 possibilités pour le deuxième. |
|||||||||||||||||||||||||||||||||||||||||
|
|
||
|
Soit E un ensemble fini de n
éléments et p un entier tel que 1 Un arrangement de p éléments
de E est une p-liste d'éléments de E deux à deux distincts |
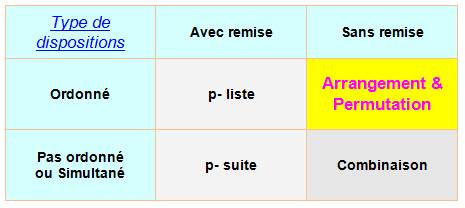
Voir Types de dispositions – Tableau complet |
|
|
|
|||||||||||||||||||||||||||||||||
|
Dans la classe de 30 élèves, le mois
dernier
Chacun a décidé de se battre pour la
première place
Arrangements
|
|||||||||||||||||||||||||||||||||
Comment constituer une liste ?
|
Si
vous disposer d'un logiciel comme Maple,
la solution est immédiate. Ces
deux instructions with(combinat);
permute(5, 3) listent les arrangements de 3 parmi 5 (par exemple): [[1, 2, 3], [1, 2, 4], [1, 2, 5], [1,
3, 2], [1, 3, 4], [1, 3, 5], [1, 4, 2], [1, 4, 3], [1, 4, 5], [1, 5, 2], [1,
5, 3], [1, 5, 4], [2, 1, 3], [2, 1, 4], [2, 1, 5], [2, 3, 1], [2, 3, 4], [2,
3, 5], [2, 4, 1], [2, 4, 3], [2, 4, 5], [2, 5, 1], [2, 5, 3], [2, 5, 4], [3,
1, 2], [3, 1, 4], [3, 1, 5], [3, 2, 1], [3, 2, 4], [3, 2, 5], [3, 4, 1], [3,
4, 2], [3, 4, 5], [3, 5, 1], [3, 5, 2], [3, 5, 4], [4, 1, 2], [4, 1, 3], [4,
1, 5], [4, 2, 1], [4, 2, 3], [4, 2, 5], [4, 3, 1], [4, 3, 2], [4, 3, 5], [4,
5, 1], [4, 5, 2], [4, 5, 3], [5, 1, 2], [5, 1, 3], [5, 1, 4], [5, 2, 1], [5,
2, 3], [5, 2, 4], [5, 3, 1], [5, 3, 2], [5, 3, 4], [5, 4, 1], [5, 4, 2], [5,
4, 3]] Comme
exercice vous pouvez programmer cette fonction. Sinon,
vous pouvez utiliser le tableur. Un
exemple avec les arrangements de 4 parmi 9 (il y en a 3 024) est disponible
en List4P9.
Vous trouverez sur cette page Excel la façon de constituer une liste
personnalisée. Je vous conseille de mettre votre tableur en route avant le
téléchargement.
|
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
|
![]()