|
Système de coordonnées polaires
|
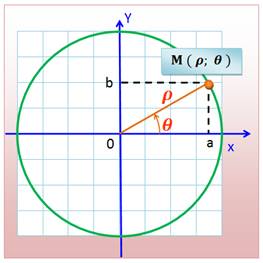
Un point M est
défini par:
 sa distance ( sa distance (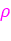 Rho) à l'origine (O) du repère et par Rho) à l'origine (O) du repère et par
 l'angle ( l'angle (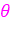 Thêta) formé par OM et l'axe des abscisses (Ox). Thêta) formé par OM et l'axe des abscisses (Ox).
Utilisé pour
rendre compte de phénomènes rotatifs ou oscillants.
Une des formes
de représentation des nombres complexes.
|
|
|
Abscisses curvilignes et angulaires
|
Abscisse
angulaire (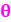 ), nom pompeux
pour nommer l'angle
orienté thêta ( ), nom pompeux
pour nommer l'angle
orienté thêta (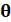 ). On le nomme aussi, argument dans le
cas de la représentation d'un nombre complexe. ). On le nomme aussi, argument dans le
cas de la représentation d'un nombre complexe.
Abscisse
curviligne (s), c'est la longueur de l'arc, plus précisément
la valeur algébrique de l'arc orienté AM.
La notion
d'abscisse curviligne s'étend à toute courbe: c'est la distance sur la
courbe à un point M à partir d'une origine. Elle est positive ou négative
selon le sens arbitraire choisi.
|
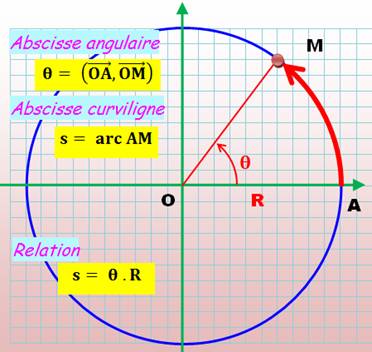
L'abscisse anglaire se mesure en radians.
L'abscisse curviligne de mesure en mètres.
|
![]()
![]()