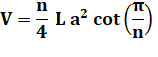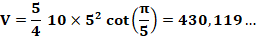|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Définition,
propriétés et amusements avec le prisme, sorte de cylindre
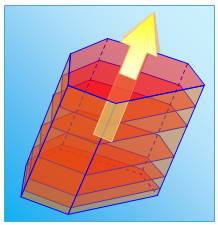
à facettes. Le prisme
est un solide engendré par un polygone
qui se déplace le long d'une droite génératrice (illustration). Le
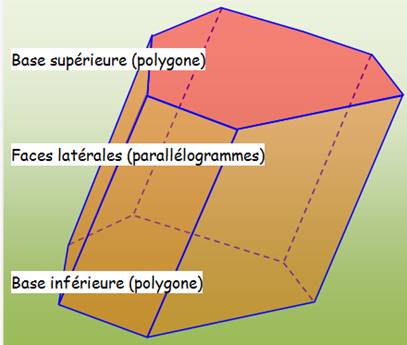
prisme, polyèdre à faces en
parallélogrammes
et bases polygonales parallèles, est
le père d'une famille nombreuse de volumes, notamment celle des parallélépipèdes lorsque la base est un quadrilatère.
Le prisme
fait partie de la famille des prismatoïdes. Quelques individus de la famille
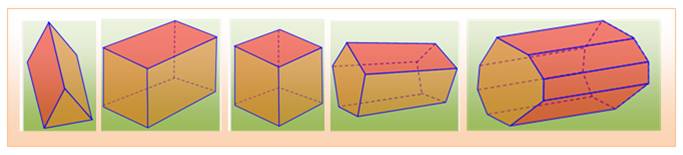
Prismes droits à base: triangle / rectangle / carré / pentagone
régulier / octogone quelconque Si la base est un polygone régulier, le prisme est régulier, sinon il est irrégulier. Si les parallélogrammes sont des rectangles le prisme est droit, sinon il est oblique. |
Anglais: Prism
Propriétés essentielles
|
Prisme
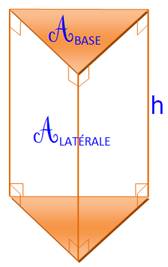
droit Aire
latérale = Périmètre × h Aire
totale = ALATÉRALE + 2 ABASE Volume = ABASE
×
h |
|
|
|
||
|
Le prisme
est un polygone qui aurait pris de l'épaisseur. Définition Le prisme
est un volume dont toutes les faces sont plates. Il est caractérisé par:
Le prisme
est un polyèdre. Le cylindre
n'est pas un prisme bien qu'un prisme à base polygonale à grand
nombre de côtés pourrait se rapprocher du cylindre. Selon la
définition du prisme, les arêtes des bases sont parallèles deux à deux et les
arêtes latérales sont toutes parallèles entre elles. |
Le prisme est le volume engendré par le mouvement de la base, translatée le long
d'une directrice (une droite parallèle à une arête latérale). |
|
|
Prisme droit et prisme oblique Dans le prisme droit, les arêtes latérales sont perpendiculaires
aux arêtes des bases. |
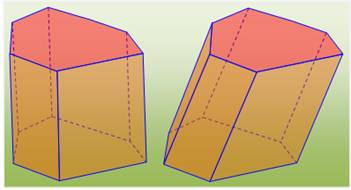
Prismes hexagonaux: droit et oblique |
|
|
|
||
|
Primes droits célèbres Le cube et le
pavé
droit (ou parallélépipède rectangle). Les bases
sont des quadrilatères: carrés
et rectangles. Note: avec une base losange
le prisme (non-droit) devient un rhomboèdre. |
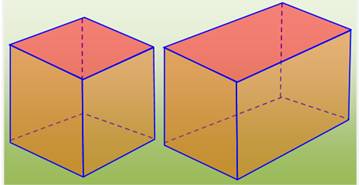
Cube et pavé droit |
|
|
Deux autres spécimens Le prime
droit triangulaire et le prisme droit pentagonal. Les bases
sont des triangles
et des pentagones. |
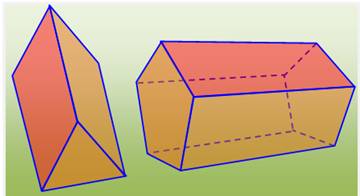
Prismes droit réguliers: triangulaire et pentagonal |
|
|
Prismes droits réguliers et
irréguliers La base d'un
prisme droit régulier est un polygone régulier; avec une base polygonale
quelconque, il est irrégulier. On a donc quatre types de prismes:
Le nom du prisme est suivi du nom du polygone de
base. Un prisme uniforme
est un prisme droit régulier dont les faces latérales sont des carrés. |
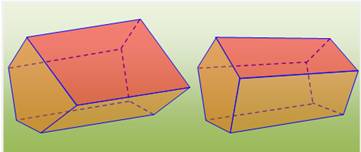
Prismes droit pentagonaux: irrégulier et régulier |
|
|
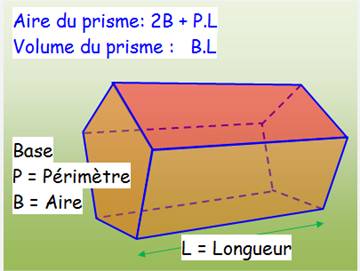
Aire du prisme droit Aire des
deux bases + aire des faces latérales. Volume du prisme droit Aire de
la base multipliée par la longueur du prisme. Volume du prisme régulier Avec a,
le côté du polygone régulier à n côtés:
Voir Aire
du pentagone / |
Volume de ce prisme pour a = 5 et L
= 10
|
|
|
|
||
|
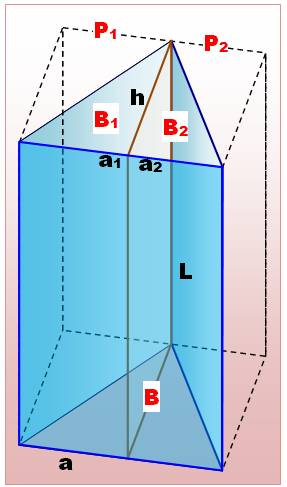
Prenons
le prisme à base triangulaire pour commencer (Illustration). Sa longueur (L) est en même temps sa hauteur. Le
triangle quelconque de la base (B) peut être découpé en deux triangles rectangles (B1
et B2) en traçant une hauteur (h). Le volume
des parallélépipèdes droits P1 et P2
est égal à: L.h.a1 et L.h.a2.
Le volume
des prismes droits avec B1 et B2 est égal à: ½ L.h.a1 et ½ L.h.a2. Le volume
du prisme droit avec B est égal à la somme des deux: V = ½ L.h(a1
+ a2) ) = ½ L.h a = B . L Ce raisonnement est applicable au prisme droit à base
polygonale quelconque en découpant le polygone en autant de triangles
rectangles que nécessaire. Le volume du prisme droit est égal au produit de l'aire de la base par
la longueur du prisme droit: V = B x L. Formule analogue à celle du cylindre
droit |
|
|
|
|
||
|
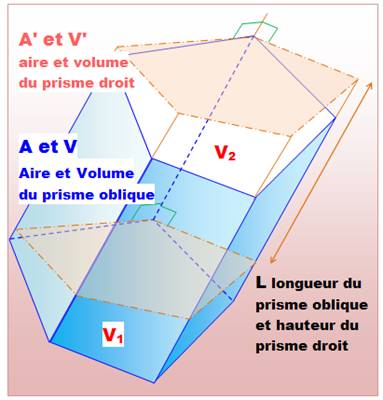
Un prisme
oblique (bleu). Un plan
perpendiculaire à toutes les arêtes et s'appuyant sur l'un des sommets
(rose). C'est possible car toutes les arêtes sont parallèles. Ce plan
perpendiculaire s'appelle la section droite. Le volume
formé par les arêtes et les deux plans roses est un prisme droit dont le
volume est égal à A' x L (aire de la base du prisme droit fois sa hauteur). Les
volumes tronqués en haut et en bas (V1 en moins et V2
en plus) sont égaux et se compensent. Le volume (V) du prisme oblique est
égal au volume (V') du prisme droit. C'est-à-dire: V = A' x L, le produit de
la section droite par la longueur du prisme oblique. |
Transformation du prisme oblique en
prisme droit
Le volume du prisme oblique est égal à celui du prisme droit, soit le
produit de l'aire de la section droite du
prisme oblique par sa longueur. |
|
|
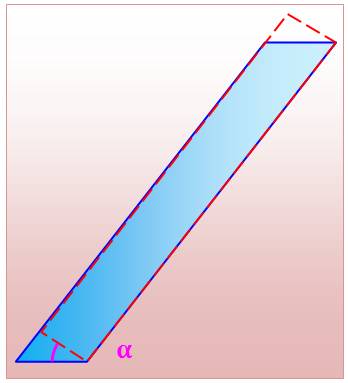
Sur cette
illustration simplifiée, le volume bleu se recompose en volume rouge
pointillé en basculant la partie du bas en haut. La
hauteur est la même. Par contre, la base est projetée sur la section droite
avec un angle alpha. Aire de la section droite: il s'agit de la projection orthogonale de
la base sur un plan faisant un angle alpha entre le plan de la base et le
plan de la section |
Illustration du principe de calcul
Aire section droite = aire base |
|
|
Volume du prisme oblique. |
V = A . L cos |
|
|
|
||
|
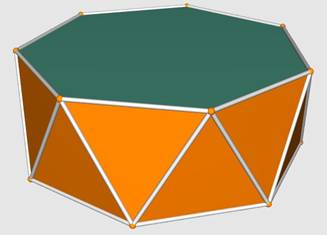
Un
antiprisme est un prisme dont on aurait fait pivoter l'une des bases; les
faces devenant des triangles. Un antiprisme droit est formé à partir:
Un antiprisme uniforme est un antiprisme dont les
faces sont des triangles
équilatéraux. |
Antiprisme heptagonal Source image: Antiprism.com |
|
|
Ce solide est
référencé en tant que prisme (optique)
sans autre précision. Il peut prendre d'autres formes que le prisme géométrique. |
Voir Arc-en-ciel
|
|
|
|
PRISM: a solid with two congruent (identical) parallel faces, where any cross section parallel to those faces is
congruent to them. A prism is a solid that has two faces that
are parallel and congruent. These are called the bases
of the prism. If you take any cross section of a prism parallel to those
bases by making a cut through it parallel to the bases, the cross section
will look just like the bases. |
|
![]()
|
Suite |
|
|
Aussi |
|
|
Cette page |
![]()