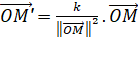|
Inversion de figures par rapport à un cercle –
Exemples
|
Approche |
Comment
transformer un dessin tel que, |
|
Définition |
Un
point O, centre de l'inversion ou pôle de l'inversion; Un
nombre réel k, puissance de l'inversion; L'inversion associe au point M
un point M' tel que:
Relation vectorielle et
produit des valeurs algébriques |
Voir Exemple de
construction / Approche
et développements sur l'inversion
![]()
|
|
-
bijective: points
qui se correspondent un à un; -
involutive: appliquée deux fois, on retrouve la figure
de départ.
-
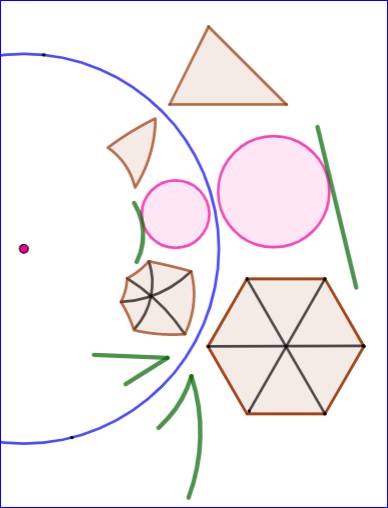
L'image d'un cercle est généralement un cercle, sauf si
le pôle est sur le cercle, auquel cas l'image est une droite (ou cercle avec
rayon infini; notion de cercle généralisé). -
L'image d'un point interne au cercle est externe au
cercle et plus il est proche du centre plus ile est envoyé au loin; et
réciproquement. |
|
Famille |
|
![]()
|
Anglais |
OP x OP' = r²
preserves angles;
and maps generalized
circles into generalized circles. |
|
En savoir plus |
Voir suite en
cliquant sur les mots de l'en-tête
|
![]()
![]()
|
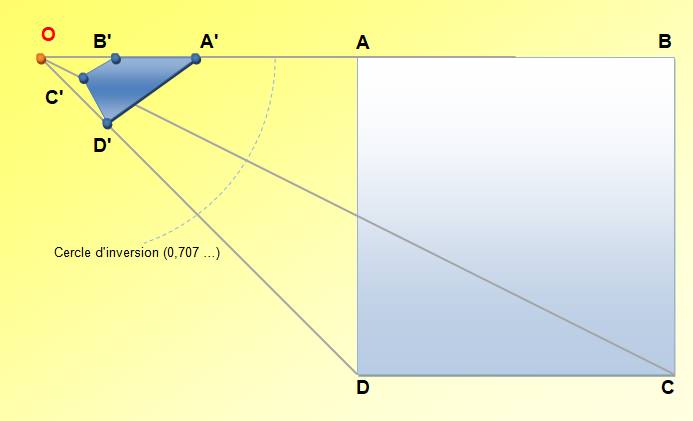
Inversion d'un carré L'inversion des quatre sommets (sans les
côtés)
k = 0,5 OA = 1; OA' = 0,5 / 1 = 0,5 OB = 2; OB' = 0,5 / 2 = 0,25 OD² = 1² + 1² =
2; OD' = 0,5 / 1,414 = 0,35 OC² = 2² + 1² =
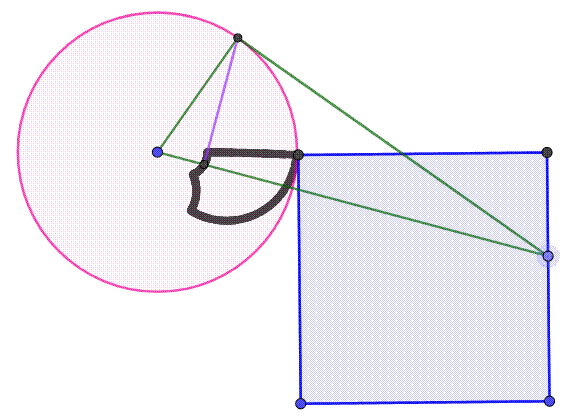
5; OD' = 0,5 / 2,236 = 0,22 L'inversion du carré avec ses côtés La transformée
d'un segment est généralement un arc de cercle.
|
![]()