NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/06/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	LOGIQUE
Débutants Logique	Domaines			Glossaire Logique
INDEX Logique	Dualité	Logique de Boole	Logique formelle	Logique floue
	Raisonnement	Intelligence	Systèmes experts	Incomplétude
		Sommaire de cette page >>> Valide ou non: vrai / faux >>> Éléments de connexion logique >>> Propositions >>> Raisonnement déductif >>> Raisonnement par l’absurde >>> Raisonnement inductif >>> Raisonnement par récurrence >>> Implication

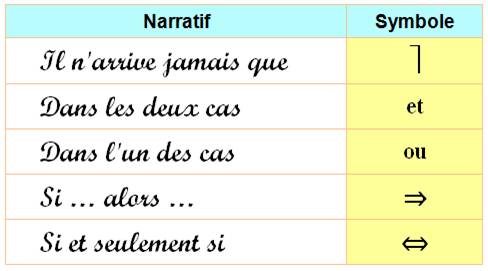
LOGIQUE FORMELLE

ou logique du raisonnement

Logique des déductions:

" Si c'est la saison et s'il pleut,

alors je vais cueillir des champignons "

La logique formelle cherche à déterminer si un raisonnement est valide ou non.

  symbole de déduction: on en déduit que, donc…

Anglais: Symbolic logic

En un scandaleux raccourci: la logique de premier ordre est un langage formel mathématique utilisant des propositions appelées prédicats liées par des connecteurs (ou opérateurs) logiques comme et, ou, si. La logique fournit des résultats déductifs vrais ou faux en combinant des propositions déterminées vraies ou fausses.

Yannick Grannec – La Déesse des petites victoires

Voir Pensées & humour

VALIDE OU NON: VRAI / FAUX
Raisonnement valide Si le fleuve monte (A), ma maison est inondée (B). Le fleuve monte (A). Déduction: ma maison est inondée (B). Cette déduction est valide.	Si A alors B A B Vrai
Raisonnement NON valide Si le fleuve monte, ma maison est inondée. ma maison est inondée. Déduction: le fleuve monte. Il y a peut être d'autres raisons (un déluge!).	Si A alors B B A Faux
Raisonnement NON valide Chirac est Président ou Jospin Premier Ministre. Déduction: Chirac est Président. On ne peut pas en tirer une conclusion, donc:	A ou B A Faux
Raisonnement valide Chirac est Président ou c'est Jospin. Ce n'est pas Jospin. Déduction: Chirac est Président.	A ou B B A Vrai

ÉLÉMENTS DE CONNEXION LOGIQUE

Voir Connecteurs

PROPOSITIONS

Une proposition est une phrase contenant une affirmation, vraie ou fausse. La nuit tous les chats sont gris. Les chevaux sont des équidés. La vérité sort de la bouche des enfants. Je suis un menteur. a^n + b^n = c^n n’existe pas pour n > 2 (Fermat-Wiles) La logique est l’étude de l’enchaînement de propositions par raisonnement. Un raisonnement est une suite de propositions liées par des conditions logiques qui aboutissent à une conclusion.

RAISONNEMENT DÉDUCTIF
Analogie avec enquête policière. Avec des indices, ou des hypothèses, de déductions en déductions, on essaie de résoudre l’énigme ou, en maths, de démontrer la propriété étudiée. Du général au particulier.

Voir Exemple: enquête concernant les trois hôtels

RAISONNEMENT par l’ABSURDE ou APAGOGIE Reductio ad absurdum
On suppose que la conclusion est fausse (le théorème est faux), et On démontre que cela conduit à une contradiction. Exemples Célèbre démonstration (simple) d’Euclide prouvant qu’il y aune infinité de nombre premiers. On suppose donc comme hypothèse que cette assertion est fausse: il y a une quantité finie de nombres premiers. Démonstration de Niels Abel concernant les équations quintiques.

Voir q et r sont uniques dans la division /  Humour Absurde

RAISONNEMENT INDUCTIF
Par généralisation ou par extrapolation Du particulier au général. Comme le ph ysicien qui observe les faits et en tire une loi générale. Le raisonnement par récurrence est inductif.

RAISONNEMENT par RÉCURRENCE

S’applique aux propositions qui ont des successeurs (n, n + 1, n + 2 ...); Comme c'est le cas pour les nombres entiers. Il comprend deux étapes : On démontre que la propriété est vraie au début, pour n = 1, par exemple; Puis, on démontre que, si elle vraie pour n, alors elle est vraie pour n = n + 1. En effet, par phénomène de cascade : Si la propriété est vraie pour 1, elle l’est aussi pour 2, puis pour 3 … Elle donc vraie pour tout n. Exemple

Proposition	1 + 2 + 3 … + n = n (n + 1) / 2
Étape 1 Vraie pour 1 ?	1 = 1 (1 + 1) / 2 C’est vrai !
Étape 2 Suite ?	Si admise pour n, est-elle vraie pour n+1 ?
Vraie (hypothèse)	1 + 2 + 3 … + n =	n (n + 1) / 2
Ajoute n+1 à chaque membre	1 + 2 + 3 … + n + (n + 1) =	n (n + 1) / 2 + (n + 1)
Même dénominateur		n (n + 1) / 2 + 2 (n + 1) / 2
Ce que l’on cherche à prouver		(n + 1) (n + 2) / 2

Suite sur le raisonnement par récurrence / Voir Addition de Gauss

IMPLICATION

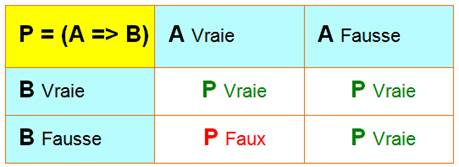
Mode de raisonnement La proposition suivante: Une proposition A implique une proposition B Notée: A => B n’est fausse que si A est vraie et B est fausse. Table de vérité Exemple « Il pleut => la route est mouillée » est une proposition vraie. Mots-clés Si … alors Il suffit que … Il faut que… Il faut et il suffit que… La condition est nécessaire et suffisante Deux possibilités de démonstration : On part de A et on aboutit à B. ou Contraposition On démontre que si B n’est pas vraie, alors A n’est pas vraie.

Voir Implication logique

Suite	Voir haut de page Démonstrations – Types Logique – Index Systèmes experts Syllogismes
Voir	Auto - Références Énigmes et paradoxes Fractales Groupes sanguins Intégrammes Intelligence artificielle Logique et dualité Outils de la logique Raisonnement Tiers exclu
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Logique/LogForm.htm