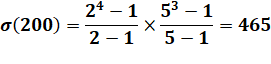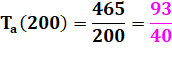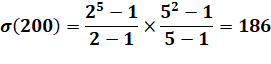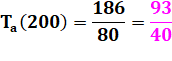Paires de nombres amis

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/10/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Diviseurs
Débutants Nombres parfaits	Types de nombres selon leurs diviseurs			Glossaire Diviseurs
INDEX Décomposition Diviseurs Types de nombres	Présentation	Parfait	Presque parfait	Amiables
	de 1 à 100	Démonstration	Unit. Parfait	Fiancés
	Admirable	Zumkeller	Amis / Solitaires	Sublimes
		Sommaire de cette page >>> Approche >>> Liste des paires d'amis

Nombres AMIS / Nombres SOLITAIRES

Nombres qui partagent le même taux d'abondance, lequel est le rapport entre la somme des diviseurs et le nombre lui-même.

Ne pas confondre avec les paires amiables >>>

Exemple: les nombres 80 et 200 sont amis

Anglais: Friendly pair / Solitary numbers

Approche
On s'intéresse à la somme des diviseurs d'un nombre (noté sigma). Son taux d'abondance est le rapport entre cette somme et le nombre.
Lorsqu'un autre nombre possède le même taux d'abondance, on dit qu'ils sont amis. C'est le cas des nombres 80 et 200.

Liste des paires d'amis
94 paires d'amis jusqu'à 5000 Ami 1, Ami 2, numérateur, dénominateur du taux d'abondance. Attention Ce sont les paires entre nombres compris entre 1 et 5 000. Il peut exister d'autres paires avec de plus grands nombres.	[6, 28, 2, 1], [6, 496, 2, 1], [12, 234, 7, 3], [28, 496, 2, 1], [30, 140, 12, 5], [30, 2480, 12, 5], [40, 224, 9, 4], [42, 3472, 16, 7], [56, 3724, 15, 7], [60, 1170, 14, 5], [66, 308, 24, 11], [78, 364, 28, 13], [80, 200, 93, 40], [84, 270, 8, 3], [84, 1488, 8, 3], [84, 1638, 8, 3], [102, 476, 36, 17], [114, 532, 40, 19], [120, 672, 3, 1], [132, 2574, 28, 11], [135, 819, 16, 9], [138, 644, 48, 23], [140, 2480, 12, 5], [150, 700, 62, 25], [174, 812, 60, 29], [186, 868, 64, 31], [204, 3978, 42, 17], [222, 1036, 76, 37], [228, 4446, 140, 57], [240, 600, 31, 10], [246, 1148, 84, 41], [252, 4464, 26, 9], [258, 1204, 88, 43], [270, 1488, 8, 3], [270, 1638, 8, 3], [282, 1316, 96, 47], [318, 1484, 108, 53], [330, 1540, 144, 55], [354, 1652, 120, 59], [360, 2016, 13, 4], [366, 1708, 124, 61], [390, 1820, 168, 65], [402, 1876, 136, 67], [426, 1988, 144, 71], [438, 2044, 148, 73], [440, 2464, 27, 11], [474, 2212, 160, 79], [498, 2324, 168, 83], [510, 2380, 216, 85], [520, 2912, 63, 26], [534, 2492, 180, 89], [540, 3276, 28, 9], [560, 1400, 93, 35], [570, 2660, 48, 19], [582, 2716, 196, 97], [606, 2828, 204, 101], [618, 2884, 208, 103], [642, 2996, 216, 107], [654, 3052, 220, 109], [678, 3164, 228, 113], [680, 3808, 81, 34], [690, 3220, 288, 115], [720, 1800, 403, 120], [726, 3388, 266, 121], [750, 3500, 312, 125], [760, 4256, 45, 19], [762, 3556, 256, 127], [786, 3668, 264, 131], [822, 3836, 276, 137], [834, 3892, 280, 139], [858, 4004, 336, 143], [864, 936, 35, 12], [870, 4060, 72, 29], [880, 2200, 279, 110], [894, 4172, 300, 149], [906, 4228, 304, 151], [924, 2970, 32, 11], [930, 4340, 384, 155], [942, 4396, 316, 157], [978, 4564, 328, 163], [1002, 4676, 336, 167], [1014, 4732, 366, 169], [1038, 4844, 348, 173], [1040, 2600, 651, 260], [1074, 5012, 360, 179], [1086, 5068, 364, 181], [1092, 3510, 112, 39], [1360, 3400, 837, 340], [1428, 4590, 48, 17], [1488, 1638, 8, 3], [1520, 3800, 93, 38], [1680, 4200, 124, 35], [1840, 4600, 279, 115], [4320, 4680, 7, 2], …
Nombre sûrement amis	6, 12, 24, 28, 30, 40, 42, 56, 60, 66, 78, 80, 84, 96, 102, 108, 114, 120, 132, 135, 138, 140, 150, 168, 174, 186, 200, 204, 210, 222, 224, 228, 234, 240, 246, 252, 258, 264, 270, 273, 276, 280, 282, 294, 300, 308, 312, 318, 330, 348, 354, 360, 364, 366, 372.
Triplets d'amis (exemples)	(66, 308, 5456), (78, 364, 6448), (102, 476, 8432), (114, 532, 9424), (270, 1488, 1638), (2160, 5400, 13104), (9360, 21600, 23400), (4320, 4680, 26208), …
Quadruplets d'amis (exemples)	(3612, 11610, 63984, 70434), (3948, 12690, 69936, 76986), …
Quintuplets d'amis (exemples) Chacun testé jusqu'à 1 million	(30, 140, 2480, 6200, 40640), (84, 270, 1488, 1638, 24384), (420, 7440, 8190, 18600, 121920), …
Nombres parfaits	(6, 28, 496, 8128, …) Tous les nombres parfaits sont amis. Leur taux d'abondance est égal à 2.

Note: Les recherches de triplets … ne sont pas exhaustives.

Nombres solitaires

Un nombre solitaire n'a pas d'amis.

Parmi eux, on trouve :

tous les nombres premiers;

tous ces nombres à une puissance; et

tous les nombres avec PGCD (n, sigma(n) ) = 1.

Voir la liste ci-contre.

Il n'est pas facile de conclure sur le statut d'un nombre: ami ou solitaire ? Malgré des recherches jusqu'à 10³⁰, on ne sait pas si le nombre 10 est solitaire.

Eric Weisstein cite le cas de la paire 24, 91 963 648 (taux d'abondance 5/2), prouvant que parfois, il faut explorer vers les grands nombres.

Nombres solitaires connus

1, 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 21, 23, 25, 27, 29, 31, 32, 35, 36, 37, 39, 41, 43, 47, 49, 50, 53, 55, 57, 59, 61, 63, 64, 65, 67, 71, 73, 75, 77, 79, 81, 83, 85, 89, 93, 97, 98, 100, 101, 103, 107, 109, 111, 113, 115, 119, 121, 125, 127, 128, 129, 131, 133, …

Nombres probablement solitaires (pas de preuve)

10, 14, 15, 20, 22, 26, 33, 34, 38, 44, 46, 51, 54, 58, 62, 68, 69, 70, 72, 74, 76, 82, 86, 87, 88, 90, 91, 92, 94, 95, 99, 104, 105, 106, …

Suite	Paires amiables Suite aliquote Nombres sublimes Couples de nombres en puissance Types de nombres par ordre alphabétique Voir haut de page
Voir	Calcul mental – Index Nombres bons Nombres économes, équidistants et prodigues Théorie des nombres – Index Types de nombres selon leurs diviseurs
DicoNombre	Nombre 200
Sites	Friendly Numbers – Wolfram MathWorld Solitary Numbers – Wolfram MathWorld OEIS A074902 - Known friendly numbers OEIS A050972 – Smaller member of friendly pairs ordered by smallest maximal element OEIS A050973 – Larger member of friendly pairs ordered by smallest maximal element OEIS A014567 – Nombres solitaires "purs"
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/AmiPaire.htm