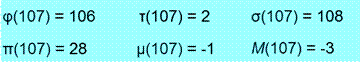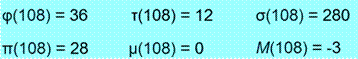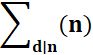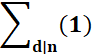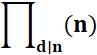|
|||||||||||||||||||||||||||||||||||
![]()
|
INVENTAIRE des FONCTIONS ARIT Certaines fonctions
sont bien connues. Elles ont été vues
dans le début de ce texte
Il en existe beaucoup
d'autres Il
est difficile d'arrêter l'imagination des mathématiciens …
|
|
|
|||
|
Exemples
avec 107 (premier) et 108 (composé)
Explications |
|||
|
|
Totient,
ou Indicateur
d'Euler |
Quantité
d'entiers inférieurs à x et
n'ayant aucun diviseur commun avec x. The function
phi will compute the totient function of n, which is the number of positive
integers not exceeding n and relatively prime to n. |
|
|
|
Tau de n |
Quantité de diviseurs. The function tau (n)
will compute the number of positive divisors of n. |
|
|
|
Sigma de n |
Somme des diviseurs. The function
sigma(n) will compute the sum of the positive divisors of n |
|
|
|
Pi de n |
Quantité
de nombre premiers p The function
pi(n) computes the number of prime numbers less than or equal to the given
integer n. |
|
|
|
Mu de n Fonction
de Moebius (Möbius) |
Caractérise
la quantité de facteurs. The function
mobius(n) gives the Mobius function of n (lattice of divisors). It returns 1,
-1, or 0 depending on the factorization of n. |
|
|
M(n) |
M de n Fonction
de Mertens |
Cumul de M(n) is the
count of square-free integers up to n that have an even number of prime
factors, minus the count of those that have an odd number. |
|
Voir Table complète des six fonctions
pour n de 0 à 200
|
|
||
|
Pour un nombre n donné |
|
|
|
FACTEURS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
M(n) |
|
|
DIVISEURS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E(n) |
|
|
|
A(n) |
|
|
|
G(n) |
|
|
|
H(n) |
|
|
PUISSANCE |
|
|
|
|
|
|
|
|
|
|
|
CHIFFRES |
|
|
|
|
||
|
|
||
![]()
|
Pour tous les nombres n inférieur ou égaux à x |
|
|
|
FACTEURS |
|
|
|
|
S(x) |
|
|
|
E(x) |
|
|
|
O(x) |
|
|
DIVISEURS |
|
|
|
|
D(k) |
|
|
|
p(n) |
|
|
|
|
|
|
||
|
Diviseurs unitaires |
d est un
diviseur unitaire si (d, n/d) = 1. Exemple
|
|
|
Squarefree |
Nombre
dont aucun des facteurs n'est répété. Exemples
|
|
|
|
|||
|
Notations |
Qui veut dire |
Exemples |
|
|
n = … |
Produit des facteurs p |
12 = 22 . 3 360 = 23 . 32
. 5 |
|
|
d |
d divise n |
3|12 5|360 |
|
|
|
Somme des diviseurs d |
= 1+2+3+4+6+12 = 28 |
|
|
|
Somme de la valeur 1 |
= 1+1+1+1+1+1 = 6 |
|
|
|
Produit des diviseurs d |
= 1x2x3x4x6x12 = 1728 |
|
|
|
||
|
SOMME de CARRÉS |
|
|
|
|
h(n) |
|
|
|
f(n) |
|
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/APROF/FoArithm.htm
|
![]()