NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/03/2015 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Dénombrement
Débutants Dénombrement	Études de cas			Glossaire Général
INDEX Dénombrement Vue globale Probabilités	Élèves et langues	Trois dés et une urne	Qualité usine
	Terminale	Sommaire de cette page >>> Rappel du vocabulaire >>> Arbre pondéré >>> Bilan 1 >>> Garçons et filles >>> Bilan 2 >>> Algèbre de l'arbre pondéré

Élèves: garçons et filles

& Langues: anglais et allemand

Introduction à l'utilisation des arbres pondérés pour résoudre des problèmes de probabilités. Cette méthode graphique est un outil au même titre que le dessin de la division qui permet le calcul d'un quotient. Ce qui veut dire que l'arbre pondéré est considéré comme une méthode licite de démonstration.

Rappel du vocabulaire
Nom	Définition	Exemple
Univers	Ensemble de toutes les possibilités. Noté oméga:	Avec un dé, l'univers est: = {1, 2, 3, 4, 5, 6}
Issue	Possibilité, éventualité, cas possible.	Au lancement du dé, six issues sont possibles. Probabilité de chacune = 1/6.
Événement	Une issue ou Un ensemble d'issues.	L'événement A est l'obtention d'un multiple de trois avec un dé. A = {3, 6}. Probabilité = 2/6 = 1/3. L'événement B est l'obtention d'un nombre inférieur à 4. B = {1, 2, 3}. Probabilité = 3/6 = 1/2. L'événement C est l'obtention du 1. C = {1}. Probabilité = 1/6.
Hypothèses	A = {3, 6} B = {1, 2, 3} C = {1}
Év. contraire	Les autres issues de l'univers. Noté	= {1, 2, 4, 5} Probabilité = 4/6 = 2/3
Év. certain	= univers.	Probabilité = 1
Év. impossible	= rien = ensemble vide	Probabilité = 0
Év. incompatibles	Qui ne peuvent pas se réaliser simultanément.	Probabilité = 0
Intersection (ET)	Toutes les éventualités qui sont en même temps dans A et dans B.	(aussi A ET B) Probabilité = 1/6 Propriété:
Union (OU)	Toutes les éventualités qui appartiennent à au moins un des deux événements.	(aussi A OU B) Probabilité = 4/6 Propriété:
Loi équirépartie	Univers de n issues, alors: probabilité de chaque issue = 1/n	Cas du dé cubique régulier: chacune des issues est équiprobable. Sur un très grand nombre de lancés, chaque face sortira avec la autant de fois que les autres.
Cardinal	Quantité d'éléments dans un ensemble.	Card () = 6 Card (A) = 2
Probabilité	Quantité de cas favorables sur quantité de cas possibles.

Arbre pondéré
Données Action 1: je lance un dé. Action 2: je lance le dé une nouvelle fois. Événement D = le 6 sort avec le premier dé. Probabilité de 1/6 Événement E = le 6 sort avec le deuxième dé. Probabilité de 1/6 Calcul classique de probabilité Les lancés sont totalement indépendants. Le premier lancé offre six issues, et pour chacune, le second en donne six; soit 36 issues au total. Card () = 36 Le double-six ne sort qu'une seule fois. Card (double-six) = 1 Probabilité du double six = 1/36.		Méthode de l'arbre pondéré C'est un graphe qui montre les probabilités de chaque étape dans une succession d'événements. Méthode logique Probabilité d'avoir un 6 avec l'un ET un 6 avec l'autre:
Arbre pondéré complété Il suffit de suivre les branches de l'arbre: Probabilité d'avoir: un 6 puis un 6: 1/36 un 6 et pas de 6 ensuite: 5/36 pas de 6 puis un 6 = 5/36 pas de 6 puis pas de 6 = 25 /36 Loi des probabilités totales et loi des nœuds La somme de toutes ces probabilités est égale à 1. La somme sur les branches au départ d'un nœud est égale à 1. Il est possible d'ajouter des probabilités: la probabilité d'obtenir un (seul) 6 à l'un des lancés est: 5/36 + 5/36 = 10/36 = 5/18.		1 + 5 + 5 + 25 = 36
Notion de dépendance, condition La branche E du haut est liée, conditionnée, par le fait d'avoir D. On note: PD(E), probabilité de E si D est réalisé (ou probabilité de E si D). On peut intervertir les lancé des dés. Les valeurs des probabilités sont symétriques en D et E. D'où la seconde formule.
La probabilité du deuxième événement La probabilité de E (avoir un 6 au second lancé) est égale à 1/6. .
Retournement dans l'arbre Connaissant la probabilité d'avoir un 6, je voudrais savoir quelle est la probabilité que ce soit avec le premier dé: probabilité de D sachant que j'ai E.

Bilan 1

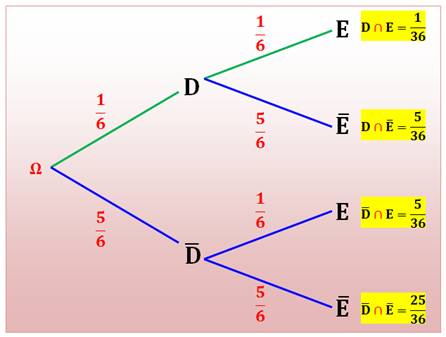
Je sais exprimer trois choses bien distinctes:

la probabilité d'un événement de départ (action 1): P(D)

la probabilité d'un événement suivant (action 2) sachant ce qui s'est passé lors de l'action 1: P_D(E) dite probabilité conditionnelle.

la probabilité que les deux événements se déroulent: P (DE)

La relation entre ces trois probabilités est explicite à la lecture de l'arbre pondéré. Elle est même symétrique:

Cette symétrie donne la possibilité de remonter l'arbre dans l'autre sens.

Garçons et filles
Problème Dans ce lycée il y a 45% de filles et 22% d'entre elles étudie l'allemand, les autres font de l'espagnol. Les garçons sont 17% à apprendre l'allemand, les autres vont en cours d'espagnol. Si je croise un élève qui va en cours d'espagnol quelle est la probabilité que ce soit un garçon? Et si c'est l'allemand?
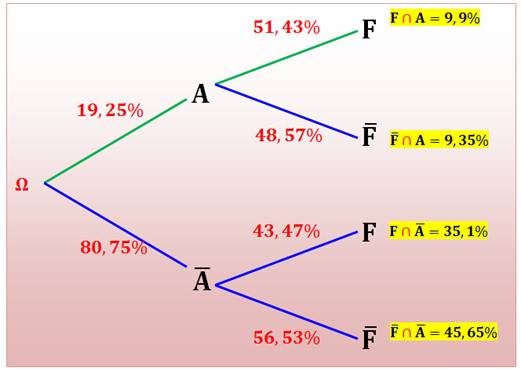
Je dessine l'arbre pondéré	F est l'événement "fille"; son contraire est "garçon" et la somme des probabilités est égale à 100% (45 + 55). A est l'événement: "l'élève apprend l'allemand". 22% des filles apprennent l'allemand donc 78% apprennent l'espagnol. Par contre, 17% des garçons apprennent l'allemand; donc 83% sont en espagnol.
Espagnol ?	La probabilité d'apprendre l'espagnol, filles ou garçons, est la somme (union) de ces deux cas:
Alors, garçon?	Sachant que cet élève étudie l'espagnol (pas l'allemand), quelle est la probabilité que ce soit un garçon (pas une fille)?
Allemand ?
Alors, garçon?
Arbre retourné Avec les calculs précédents, il est possible de compléter l'arbre retourné. Il suffit de faire en sorte que la somme des probabilités aux nœuds soit égale à 1. Exemple: il y a 19,25% des élèves qui étudient l'allemand et parmi eux, il y a 51,43% de filles.

Bilan 2

Avec les dés, nous avions deux événements identiques. Ici, nous avons des évènements très différents, mais le calcul est rigoureusement le même.

Un arbre peut facilement être retourné à condition de se souvenir des formules charnières:

L'exemple suivant va montrer l'importance de ces formules dans le cas de deux actions successives de nature très différente.

Synthèse: algèbre de l'arbre pondéré

Représentation de l'arbre pondéré et de son inverse. Les mêmes causes provoquant les mêmes effets les valeurs centrales sont égales que l'on parcoure l'arbre dans un sens ou dans l'autre. Les trois lois algébriques (ou logiques) de l'arbre pondéré 1) Loi des nœuds: au départ d'un nœud partent toutes les possibilités; la somme des probabilités est donc égale à 1 (événement certain); 2) Loi des probabilités totales: la somme des probabilités de tous les cas possibles dans cet univers est égale à 1; et 3) Loi d'équivalence des parcours: que l'on parcoure les branches (exemple en vert sur l'arbre) dans un sens (A puis B) ou dans l'autre (B puis A), la probabilité résultante est la même. Cette loi est valable quel que soit l'un des quatre parcours sur cet arbre.

Suite	Trois dés et une urne
Voir	Dénombrement – Index Football – parties Fréquences de chiffres Loi des grands nombres Oiseaux Quart de finale
Aussi	Probabilités – Index Football Jeux – Index
Cette page	http://villemin.gerard.free.fr/Denombre/aaaTermi/Ecoliers.htm