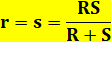Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 21/09/2023 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Quart de cercle	Deux cercles et rectangle
	Fourmi sur un pavé	Cinq cercles	Trois cercles tangents

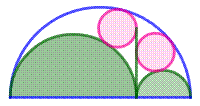
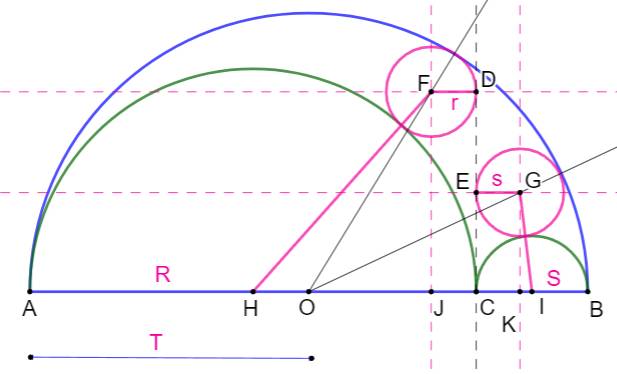
Deux cercles dans trois demi-cercles Cercles jumeaux d'Archimède Quel est le rayon de chacun des deux petits cercles roses ? L'espace entre le demi-cercle bleu et les deux demi-cercles verts s'appelle arbelos. Les deux cercles verts sont logés dans l'arbelos et ils y sont tangents.
	Sommaire de cette page >>> Deux cercles en arbelos	Débutants Géométrie Glossaire Géométrie

Deux cercles en arbelos		haut
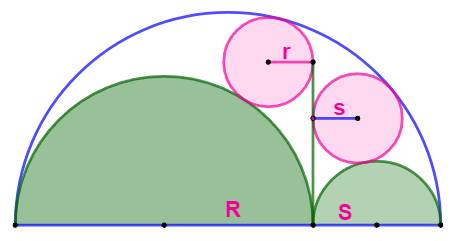
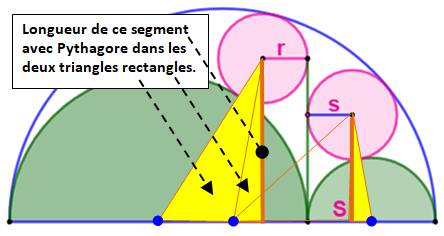
Construction Trois demi-cercles en forme d'arbelos. Deux petits cercles tangents à deux demi-cercles et à la perpendiculaire verte, cercles dits jumeaux d'Archimède Quelles sont les valeurs des rayons des deux petits cercles (r et s) en fonction des rayons des demi-cercles verts (R et S). Résultat Pistes On montre le centre (point bleu) de chacun des trois demi-cercles. En jaune à gauche, identification de deux triangles rectangles dans lesquels on applique le théorème de Pythagore pour calculer la longueur du segment vertical. Même chose à droite. On obtient ainsi une évaluation de r et une évaluation de s qu'il s'agira de comparer.

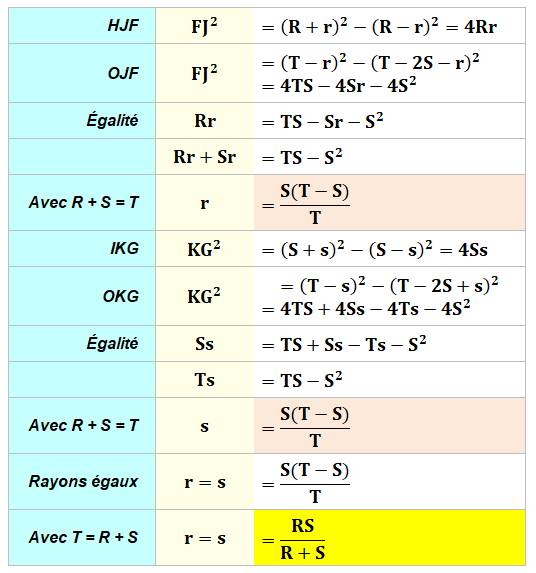
Notations

Calculs

Voir Brève 54-1068

Haut de page

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Cercles jumeaux d'Archimède – Autre démo. Sangakus (énigmes en géométrie) Lunules, croissant, arbelos Divers défis 02 Nappe sur table Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Site	Círculos gêmeos de Arquimedes – Michel Ferreira – page 20 – Document de 43 pages sur Certains cercles congrus aux cercles Jumeaux Archimède (Portugais – Brasilia).
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CinqCerc.htm