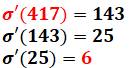|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SUITES ALIQUOTES Où
il est question de la suite des diviseurs d'un nombre et de leurs sommes à
répétition. Un nombre touchable T est un
nombre dont il existe au moins un nombre N avec une somme de diviseurs
stricts égale à T. Le nombre N est l'antécédent de T. Un nombre T peut avoir
plusieurs antécédents: objet de cette page. Le nombre 21, par exemple a trois
antécédents: 18, 51 et 91. Un nombre intouchable est un nombre qui
n'a aucun antécédent. Les nombres 2, 5, 52 et 88, par exemple, sont
intouchables. |
Voir DicoMots Maths – Suites et Séries
|
|
|
|
Rappel · Les parties aliquotes de n sont ses diviseurs propres, c'est-à-dire tous ses
diviseurs sauf n lui-même. ·
La somme des diviseurs d'un nombre n se nomme Suite
aliquote de n · Suite de nombres formée de la somme aliquote de n, puis de la somme aliquote de ce nombre, puis la somme aliquote de ce nombre, etc. Exemple pour n = 12 Exemple pour n = 20 |
|
|
|
|
|
·
En commençant par un nombre
parfait, la suite stagne! 6
=> 1 + 2 + 3 = 6 6
=> ... ·
En commençant par un nombre
amiable, la suite boucle: 220,
284, 220, 284, . . . ·
Toute chaîne amiable connue est l'extrémité d'une suite
aliquote. · Il existe d'autres boucles: les chaînes sociables ou cycles aliquotes. 14288,
15472, 14536, 14264, 12496 . . . ·
Il existe aussi des suites aliquotes qui se terminent
par un nombre parfait: Exemple:
Le
nombre de départ est un nombre aspirant. Liste
des nombres aspirants: 6, 25, 28,
95, 119, 143, 417, 445, 496, 565, 608, 650,
652, 675, 685, 783, 790, 909, 913, 1177, 1235, 1294, 1441, 1443, 1574, 1595,
1633, 1715, 1717, 1778, 2162, 2173, 2195, 2225, 2387, 2541, 2581, 2582, 2725,
2863, 3142, 3277, 3311, 3337, 3575, 3693, 3899, 3999, 4141, 4317, 4535, 4717,
4739, 4763, 4775, 4897 (en rouge, les nombres parfaits) OEIS
063769 En
bilan:
Les
boucles forment: ·
les nombres parfaits (boucle de longueur 1); ·
les nombres amiables ((longueur 2); ou, ·
les chaînes sociables (longueur n). ·
Les nombres aspirants (qui bouclent sur un nombre
parfait). |
|
|
|
But Lister les nombres aspirants y compris les
nombres parfaits. Commentaires Boucle d'exploration des nombres de 1 à 1000. Boucle d'itérations de la suite aliquote. Calcul de la somme (n) des diviseurs propres. Si n est un nombre parfait, il est enregistré
dans la liste L et la boucle est interrompue (break). Demande d'impression de la liste en toute fin de
programme. Remarque Amélioration possible en détectant deux fois de
suite le même résultat. Ajouter une alarme si la quantité d'itérations
dépasse 100. |
|
Voir Programmation – Index
|
|
|
|
·
Il existe encore des inconnues. 276,
552, 564, 660, 966, 1074,
1134, 1464,
1476, 1488, 1512,
1560, 1578, 1632, 1734, 1920, 1992. En
2010, au moins les nombres noté en rouges sont encore sous investigation. ·
On connaît une suite qui augmente pendant plus de 5000
termes. Conjecture de
Catalan-Dickson: toute suite aliquote se termine soit en une boucle soit
finit par atteindre 1 en un nombre fini d'étapes. ·
Certaines suites aliquotes peuvent croître, en moyenne,
à l'infini. D'autres rejoignent une chaîne amiable
et tournent indéfiniment en boucle. ·
De nombreuses suites aliquotes aboutissent à la paire
amiable de Paganini, 1184 et 1210. Catalan, puis Dickson, conjecturèrent que ces
suites sont bornées. Pourtant, d'après Guy, certaines suites, peut-être même
toutes celles partant d'un nombre pair, vont à l'infini. Conjecture de
Garambois n°1: Une suite aliquote démarrant sur un entier pair a une chance
sur 3 de croître indéfiniment. Voir Suites
aliquotes par Jean-Luc Garambois |
|
|
|
|
|
·
Le nombre
276 est le plus petit nombre dont la destination finale est inconnue. ·
Après 469 étapes, on obtient un nombre de 45 chiffres: 149 384
846 598 254 844 243 905 695 992 651 412 919 855 640 · Il existe cinq
nombres dont on ne connait pas encore la destinée: les Cinq de Lehmer: 276, 552, 564,
660, 966. Voir Les cent
premières itérations |
|
|
|
|
|
· Si 16 est la somme aliquote de 12. · Tout nombre possède
une somme aliquote. Mais, est-ce que tout nombre possède un antécédent. D'autres
nombres sont l'antécédent de plusieurs nombres. Records
de quantité d'antécédents: nombres hautement touchables Exemple:
le nombre 6 est la somme aliquote de
6 et de 25, soit deux valeurs; le nombre 21 est la plus petite somme aliquote
de trois nombres. 3, 1, [4] 6, 2, [6,
25] Notez que 6 est un nombre
parfait 21, 3,
[18, 51, 91] 31,
5, [32, 125, 161, 209, 221] 49, 6,
[75, 215, 287, 407, 527, 551] 73,
8, [98, 175, 335, 671, 767, 1007, 1247, 1271] 91,
9, [581, 869, 1241, 1349, 1541, 1769, 1829, 1961, 2021] 115,
10, [545, 749, 1133, 1313, 1649, 2573, 2993, 3053, 3149, 3233] 121,
13, [243, 791, 1199, 1391, 1751, 1919, 2231, 2759, 3071, 3239, 3431, 3551,
3599] 169,
15, [363, 575, 815, 1727, 2567, 2831, 4031, 4247, 4847, 5207, 6431, 6527,
6767, 6887, 7031] Suivants:
211, 301, 331, 391, 421, 511, 631, 721, 781, 841, 1051, 1261, 1471, 1651,
1681, 1891, 2101, … >>> Records
des antécédents Quel est
le plus petit nombre qui a un antécédent donné ? Le nombre 3 est l'antécédent aliquote de 4 et c'est le plus petit. Le nombre 4 est celui de 9.
La somme des diviseurs de 9 (hors 9) est
1 + 3 = 4. [1, 2], [3, 4], [4, 9], [6, 6], [7, 8], [8, 10], [9,
15], [10, 14], [11, 21], [12, 121], [13, 27], [14, 22], [15, 16], [16, 12],
[17, 39], [18, 289], [19, 65], [20, 34], [21, 18], [22, 20], [23, 57], [24,
529], [25, 95], [26, 46], [27, 69], [28, 28], [29, 115], [30, 841], [31, 32],
[32, 58], [33, 45], [34, 62], [35, 93], [36, 24], [37, 155], [39, 217], [40,
44], [41, 63], [42, 30], [43, 50], [44, 82], [45, 123], [46, 52], [47, 129],
[49, 75], [50, 40], [51, 141], [53, 235], [54, 42], [55, 36], [56, 106], [57,
99], [58, 68], [59, 265], [61, 371], [62, 118], [63, 64], [64, 56], [65,
117], [66, 54], [67, 305], [69, 427], [70, 134], [71, 201], [73, 98], [74,
70], [75, 213], [76, 48], [77, 219], [78, 66], [79, 365], [81, 147], [82,
158], [83, 237], [85, 395], [86, 166], [87, 105], [89, 171], [90, 78], [91,
581], [92, 88], [93, 267], [94, 116], [95, 445], [97, 245], [100, 124] |
|
|
|
|
|
·
The aliquot sequence starting from n is defined as
follows: ·
let sigma(n) be the sum
of divisors of n, ·
then one simply
computes f(n) =sigma(n) – n, ·
and one iterates. ·
·
Aliquot
sequences arise in iterating the sum-of-divisors
function, which assigns to a positive integer the sum of its proper divisors (i.e., excluding the number itself).
An aliquot sequence thus starts with a positive integer n, followed by s(n),
then s(s(n)), etc. ·
Cycles of length 1
come from perfect numbers. |
|
![]()
|
Contexte |
· Nombre touchables ou intouchables · Table des
suites aliquotes de 1 à 1000 |
|
Voir |
|
|
DicoNombre |
|
|
Site |
· Suites aliquotes par Jean-Luc Garambois
– Site très complet sur le sujet. · Suite aliquote et Aliquot sequence –
Wikipedia · Aliquot Sequence
– Wolfram MathWorld · Aliquot Sequence –
GeeksforGeeks – Programmes Python, Java et C · Lehmer five – Aliquot-Seiten · OEIS A115350 – Termination of the aliquot
sequence starting at n · OEIS A080907 – Numbers whose aliquot
sequence terminates in a 1 |
|
Cette page |
![]()