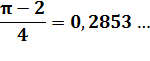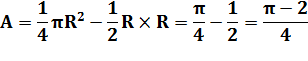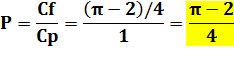triangle obtusangle

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/12/2016 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	TRIANGLES
Débutants Triangle	Types de TRIANGLES			Glossaire Triangle
INDEX Triangle	Types	Quelconque	Obtusangle	Acutangle
	Rectangle	Isocèle	Équilatéral	Partage en 7
	Sphérique	Homologique	Calabi
		Sommaire de cette page >>> Triangle obtusangle – Propriétés >>> Triangle obtusangle – Probabilité >>> Triangle obtusangle – Observations >>> Triangle obtusangle – Calculs >>> Dissection du triangle obtusangle >>> Dissection en acutangles isocèles

TRIANGLE OBTUSANGLE

C'est un triangle dont l'un des angles est obtus; les deux autres étant alors aigus.

Est-ce facile de construire un tel triangle ?

Comment disséquer un tel triangle en triangles acutangle?

Autrefois appelé aussi amblygone du latin oxygonius, à angles obtus

Anglais: Obtuse triangle / Acute triangle

Triangle obtusangle – Propriétés
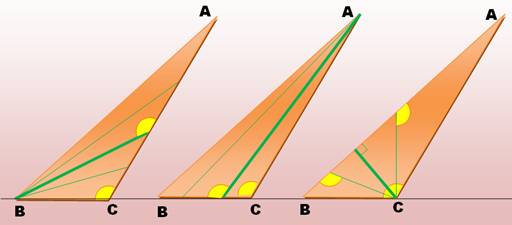
Le même triangle obtusangle, vu sous trois angles différents
Les angles L'angle obtus étant C (supérieur à 90°), les autres deux angles se partagent moins de 90°. Au mieux A = B (triangle isocèle), mais dans le cas général A < B (ou l'inverse).	C > 90 A + B < 90	B 45° 45° A < 90° 90° < C

Triangle obtusangle – Probabilité
Probabilité de former un triangle obtusangle:	= 0,28539816339744830961566084581988 …
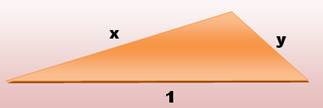
Avec deux nombres x et y, inférieurs à 1, on forme le triangle de côtés 1, x et y. Quelle est la probabilité de former un triangle obtusangle ?

Triangle obtusangle – Observations
Limitation par une droite Hypothèse sur x et y: Inégalité triangulaire et inégalités ci-dessus: Seul l’angle opposé au côté 1 peut être obtus.		x < 1 y < 1 1 < x + y < 2 Cette relation délimite deux régions du plan par une droite.
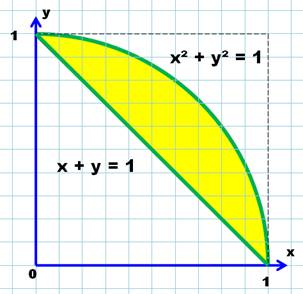
Limitation par un arc de cercle Sur un cercle, l'angle intercepté par le diamètre est un angle droit. La figure montre le lieu des points sur le cercle tels que x² + y² = 1.
Le lieu des points de coordonnées x et y qui répondent à la question sont ceux qui sont: au-dessus de la droite x + y = 1, à l’intérieur du cercle x² + y² = 1. Les cas favorables correspondent à la surface entre les deux courbes (en jaune).
Aire de la surface jaune = un quart de cercle diminué du triangle isocèle rectangle.

Triangle obtusangle – Calcul de probabilité

Valeurs possibles pour x et y

Cp = cas possibles pour x et y.

On remarque que x et y peuvent prendre toutes les valeurs à l’intérieur du carré :

Cp = R.R = 1

Valeurs favorables pour former un triangle obtusangle

Cf = cas favorables pour x et y.

On vient d'en faire le calcul ci-dessus:

Cf = ( – 2) / 4

Probabilité

La probabilité est égale au rapport des cas favorables aux cas possibles:

Dissection du triangle obtusangle

Approche

Un triangle obtusangle partagé en deux triangles, l'un d'eux reste obtusangle.

Quelle que soit le sommet une sécant (verte) partage le triangle en deux, mais l'un des triangles est obtusangle; au mieux, à partir du sommet obtus (C), on forme deux triangles rectangles.

Quelle que la manière de s'y prendre le partage d'un triangle obtusangle en deux triangles acutangles est impossible.

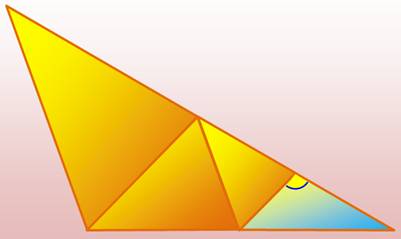
Quantité minimum

Pour disséquer un triangle obtusangle il faut sept ou huit triangles acutangles.

Toujours impossible avec quatre triangles.

Démonstration – Principe

Il faut absolument partager l'angle obtus, mais la sécante prolongée jusqu'au côté opposé va recréer un autre angle obtus.

L'idée est donc de l'arrêter quelque part dans le triangle. Bien sûr, il se forme à nouveau des angles obtus, mais …

Ce partage crée deux angles obtus.

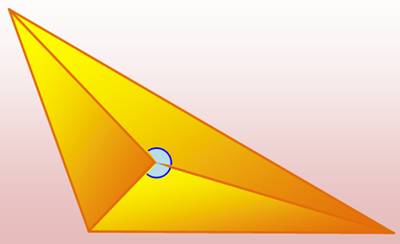
Depuis ce point, couvrant 360°, quatre sécantes pourraient partager au mieux en quatre angles droits.

Pour être sûr de n'avoir que des angles obtus, cinq sécantes sont requises; engendrant un minimum de sept triangles acutangles, les cinq du pentagone et les deux latéraux.

Note: pour réussir la partition, le point central doit ne pas être trop éloigné du sommet obtus.

Ce partage reste délicat pour n'obtenir que des angles aigus. Mais il existe toujours.

Théorème

Le plus petit nombre de triangles acutangles nécessaire pour disséquer un triangle obtusangle est sept pour C > 90° et C- A < 90 et C – B < 90; il en faut huit dans les autres cas.

Sept est un miminum, démontré par Manheimer en 1960,

Huit est suffisant démontré par V.Hoggatt et R. Denman (1961)

Contributions également de M. Gardner en 1981 et Wells en 1991.

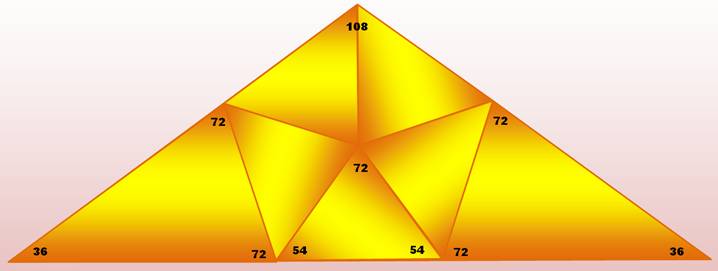
Cas particulier du triangle isocèle obtusangle (108, 36, 36) partagé en sept triangles acutangles

Voir Partage du triangle isocèle (105, 15 15)

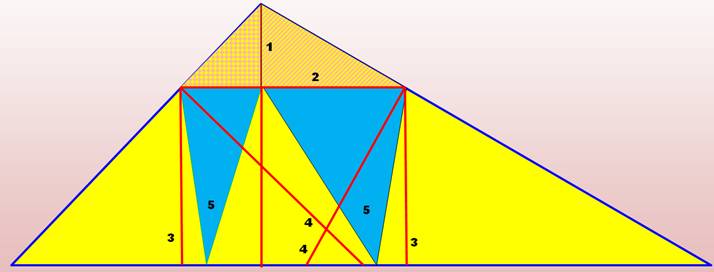
Méthode de construction

1 Descendre la hauteur à partir du sommet obtus;

2 Tracer une perpendiculaire, pas trop loin du sommet obtus;

3 Des points d'intersection descendre les perpendiculaires;

4 Des mêmes points, dessiner les perpendiculaires aux côtés; et

5 Dessiner les triangles bleus à l'intérieur des rectangles avec la pointe en bas respectivement à droite et à gauche des perpendiculaires (4).

Les deux triangles bleus, les quatre jaune en bas et les deux jaunes tramés en haut sont acutangles qui partagent le grand triangle obtusangle.

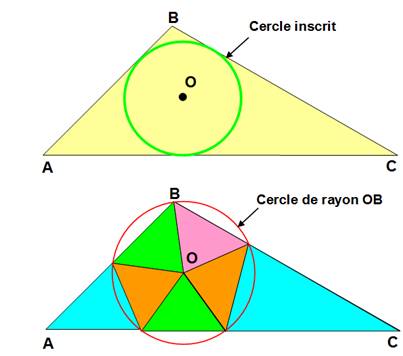
Découpe en triangles acutangles isocèles

Cette construction du découpage du triangle obtusangle peut être considérer comme une solution générale, offrant de plus des triangles acutangles isocèles.

Méthode

O est le centre du cercle inscrit.

Tracez le cercle de centre O passant par B.

Complétez comme indiqué sur la figure.

Ce procédé ne fonctionne que pour B > 90°, B-A < 90° et B-C < 90°

Sinon, tracez une droite de A qui coupe le côté opposé BC en D. Reprenez la méthode indiquée. Il y aura alors 8 pièces.