|
||||||||||||||||||||||||||||||||
![]()
|
LOGIQUE de BOOLE Logique combinatoire Logique mathématique Algèbre de Boole Calcul booléen Logique du vrai / faux du 0 / 1, utilisée dans les ordinateurs Oups! Je suis débutant … |
George Boole (1815-1864)
Britannique, mathématicien, logicien et
philosophe des mathématiques. De 1844 à 1854, Boole crée une algèbre binaire
n'acceptant que deux valeurs numériques : 0 et 1. Fondement de la logique mathématique
calculable, de la logique électronique, matérialisée d'abord par des relais
puis, aujourd'hui, sous la forme de circuits intégrés à transistors. Base du fonctionnement de l'électronique
numérique: ordinateurs, des téléphones, etc. |
Énigme logique de Martin Gardner
|
Tous
les animaux que je possède sont - Tous
sont des chiens sauf deux; - Tous
sont des chats sauf deux; et - Tous
sont des perroquets sauf deux. |
|
|
||||||||||||||||
|
Table de vérité de la
fonction ET
Exemples de
propositions La rose est une fleur, c'est
vrai. L'eau est un
liquide, ce n'est pas toujours vrai. L'eau à 20°C est liquide, c'est
vrai. S'il pleut, le sol est mouillé, c'est vrai. Le nombre 10 est premier,
c'est faux. Si un quadrilatère
a ses côtés de même longueur et si ses angles sont droits alors c'est un carré, c'est
vrai. Si un nombre est divisible
par 2 et par 3, alors il est divisible par 6, c'est
vrai. |
||||||||||||||||
|
Les
16 fonctions de deux variables Les 16 connecteurs ou 16
opérateurs |
|
||||||||
|
Fonction |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
AB =
00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
01 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
10 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
11 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
Fonction |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
AB =
00 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
01 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
10 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
11 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
Voir Connecteurs
Anglais: binary logical
connectives (voir Wikipedia à ces mots)
Voir Raisonnement
|
|
||||||||||||||||||||||||||
|
Dénomination
Illustration
" Vous
devez commencez quelque part, et vous partez de
choses admises mais indémontrables. " Ses
deux axiomes, base de sa logique étaient:
Même
si Aristote lui-même, et tous ses successeurs, admettaient les nuances: les
personnes très gentilles, celles assez gentilles, etc. Ils s'en sortaient en
définissant un seuil arbitraire passant d'une catégorie à l'autre.
|
||||||||||||||||||||||||||
Devinette classique
|
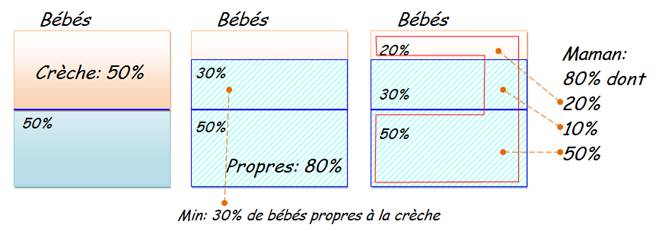
Énigme Parmi
la population de bébés étudiée: 50% vont à la crèche, 80% sont propres et 80%
savent dire maman. Quel est le pourcentage minimum de bébés propres qui vont
à la crèche et disent maman? Réponse
en image
Explications Schéma
du centre: Parmi
les bébés, au pire tous ceux qui ne vont pas à la crèche sont propres; au
mieux seuls 30% sont propres à la crèche. Schéma
de droite: au
pire, tous ceux qui ne vont pas à la crèche et qui vont à la crèche sans être
propres disent maman. Soit 70% des bébés. Il en reste au mieux 10% qui vont à
la crèche en étant propres et qui savent dire maman. |
Énigme logique de Martin Gardner – Solution
|
Énigme Tous
les animaux que je possède sont - Tous
sont des chiens sauf deux; - Tous
sont des chats sauf deux; et - Tous
sont des perroquets sauf deux. |
Solution 1 chien 1 chat 1 perroquet |
|
Satisfaisabilité booléenne
(SAT) Boolean Satisfiability Problem or Propositional Satisfiability Problem |
|
|
|
Calcul
booléen et sa résolution L'informatique
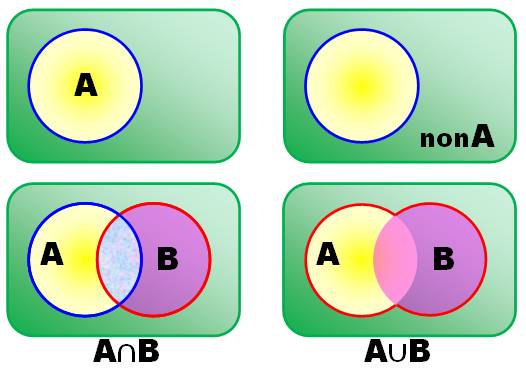
utilise le calcul booléen: Les valeurs sont (faux, vrai) ou (0, 1); Les opérateurs logiques sont: (non, et, ou). A ou B peut être satisfait par exemple avec A vrai alors A ou B est
vrai. Par contre A et non A, ne peut jamais l'être. Dans ces deux cas
simples nous avons pu décider. Avec une cinquantaine de variables ou plus, on
ne sait plus faire. La table de vérité est inimaginable et aucun algorithme
ne permet de résoudre ce problème. Calcul
booléen, une nécessité du monde moderne Le calcul
booléen a été Introduit par George Boole au milieu du XIXe siècle. Avec lui: Le raisonnement
logique passe de discours philosophique à une véritable théorie mathématique. Surtout, il devient la
base de la conception des ordinateurs. |
Problème
SAT Le calcul
booléen a constitué une révolution. Pourtant la recherche de la valeur (vrai-faux), en fonction de la quantité des variables,
coûte exponentiellement cher en temps de
calcul. Prenons seulement 50 variables binaires. Elles conduisent à 250
= 1 125 899 906 842 624 combinaisons. Imaginez pour des centaines ou des
milliers de variables … C'est le
problème de la satisfaisabilité booléenne. Important pour la conception des circuits intégrés,
la vérification des logiciels, et
des centaines de problèmes combinatoires. |
|
|
Situation Le
problème SAT est donc une interrogation pour savoir s'il existe une solution
à une série d'équations logiques. Problème de décision en logique
propositionnelle: soit une formule de logique, il s'agit de déterminer s'il
existe une valeur des variables qui rend la formule vraie. Pensez à la mise
en équations du Sudoku comme exemple. La résolution de ce genre de problème devient de plus en plus présente
dans les systèmes modernes. Par exemple, la configuration intime d'un
microprocesseur Le
théorème de Cook-Levin (1971) affirme que le problème SAT est NP-complet. Ce qui veut dire: problème
d'une grande complexité, voire insoluble. Problème NP-complet: on ne connaît
aucun algorithme déterministe polynomial pour le résoudre |
Perspective
2000 Depuis
les années 2000 et faute de pouvoir attaquer ces problèmes de front, on a
développé des algorithmes heuristiques
plutôt que des algorithmes dédiés ou l'examen, cas par cas, de la table de
vérité. Table de vérité:
tableau qui montre le résultat pour toutes les valeurs possibles des variables. Algorithme dédié:
qui suit une exécution "directe ou linéaire" et conduit vers la
solution, comme la résolution d'une équation, par exemple. Algorithme heuristique:
qui cherche progressivement à converger vers la solution en pratiquante des
essais-erreurs. Exemple:
il est plus facile de résoudre un Sudoku par heuristique qu'avec un
algorithme classique. Interrogation:
les mathématiciens ne comprennent toujours pas pourquoi ces algorithmes
marchent si bien sur autant de cas pratiques ! |
|
Voir Neuronique / Sept
problèmes du siècle / 21 problèmes
de Karp
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Sites sur le problème SAT |
|
|
Cette page |
![]()