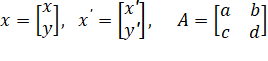|
Transformations et
structures
|
Un principe directeur des
mathématiques modernes tient en cette leçon : lorsque vous avez affaire à une
entité S munie d'une certaine structure,
essayez de déterminer son groupe d'automorphismes, le groupe des transformations de ses éléments qui préservent
les relations structurales. Vous pouvez espérer gagner une profonde
compréhension de la constitution de S de cette manière. Hermann
Weyl |
|
Approche |
|
|
Définition |
Transformation: opération qui
modifie une figure par déplacement ou
changement d'échelle ou passage à travers des miroirs. Application du plan ou
de l'espace sur lui-même associant deux objets géométriques,
points ou figures.
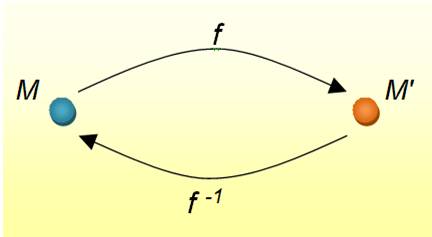
Transformation ponctuelle dans le plan: à tout point M correspond un point M' situé dans
le même plan. Le point de départ est l'antécédent. Le point d'arrivée est l'image ou le
transformé. |
![]()
|
Selon l'opération effectuée: Translations (glissement) Rotations (ça tourne) Symétries (vue à travers un miroir) et Homothéties (effet de zoom) Similitudes (effet de zoom et déplacement) Selon les éléments conservés dans la figure image: Transformations homographiques: droites Transformations affines: parallélisme Similitudes: rapports de distances
Isométries: distances et angles Déplacements: distances et angles
orientés
|
|
|
Voir |
Exemples |
![]()
|
Propriété |
|
![]()
|
Groupe |
-
une loi de composition
interne: La composition de deux transformations de E
est une transformation appartenant à E. -
un élément neutre La transformation identité I qui transforme
une figure en elle-même est l'élément neutre; la composition d'une
transformation T avec I est la
transformation T. -
une application inverse Toute transformation T de E a un inverse T’
dans E tel que la composition de T et T’ soit égale à I.
-
Il existe des sous-groupes
dont les propriétés particulières permettent de classer les différentes
transformations. Par exemple, le sous-groupe principal
comprend les rotations, les translations et les symétries orthogonales. |
![]()
|
Famille |
Un
point M' du plan est l'image d'un seul point M du plan: M'
= f(M) Alors,
l'application f est une bijection. Cette
bijection particulière d'une partie du
plan dans lui-même est baptisée: transformation. Application => bijection => transformation
Encore
une marche arrière est nous revenons sur nos pas, le point M
est transformé en M', d'où cette écriture: ( f -1) -1 = f
|
![]()
|
Vue d'ensemble |
|
|
Tableau simple
Voir Tableau plus complet Voir Translation / Rotation
/ Symétrie / Similitude / Homothétie
/ Isométrie |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Anglais |
Transformation refers to a function from X to itself which
preserves its algebraic or geometric structure Examples of
transformations: rotations, reflections, translations Such
operations can be performed using algebra (matrices) Transformation of the plane: let S be the set of points in the plane, a transformation of the pane
is a one-to-one mapping from S to S. The most
important transformation is the linear transformation which are
those that can be represented by linear equations. The linear
transformation T maps the point P (x,y) to the point P'(x', y'), where: x'=
ax + by + h and y' = cx + dy = k When h = k =
0, the origin O is a fixed point, then the transformation can be written X =
A.X', where
See Matrices |
![]()
|
En savoir plus |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosT/Transfor.htm |
![]()
![]()
|
Application (opération de
E dans F)
|
|
-
Transformation homographique (conserve les droites; ex: carré devient
trapèze)
Note: Involution (appliquée
deux fois, donne le dessin d'origine; ex: symétrie)
¨
Similitude directe (conserve les angles orientés) et
similitude indirecte ou inverse ou rétrograde (conserve les angles orientés)
-
Rapport quelconque -
Rapport 1:
identité -
Rapport -1: rotation d'un demi-tour ¨
Isométrie ou transformation
coïncidente (conserve
les distances; ex: lune reste une lune de même taille, mais ailleurs et
éventuellement retournée)
-
Identité (ne change
pas; ex rotation d'un tour complet)) -
Translation (glisse
définie par un vecteur) -
Rotation (pivote) – composition de deux réflexions
-
Symétrie
orthogonale
ou axiale ou réflexion ou par rapport à une droite
|
|
|
![]()
Transformation vue par Escher: effet de miroir
|
Faites
descendre ou monter cette image
sur votre écran pas à pas à l'aide de la molette de votre souris; L'image
s'anime! Un effet qu’Escher n'avait sans doute pas prévu. |
![]()