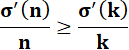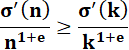|
|||||||||||||||||||||||
![]()
|
NOMBRES et leur structure Diviseurs et ADDITION
|
Selon
la somme par rapport au nombre

Diviseurs
stricts et diviseurs propres sont synonymes. On préfèrera le premier. Voir
Diviseur
Rappel, vous pouvez
consulter la Page débutants
|
|
|||
|
Déficients ou défectueux |
Parfaits |
Abondants ou excessif |
|
|
Presque parfaits |
Semi-parfaits, Multiparfaits |
Quasi parfaits Hautement abondant, Superabondants, Colossalement
Abondants, Étranges ou tordus |
|
|
|
Sublimes |
|
|
|
Par exemple |
||
|
Nombre déficient |
La somme de leurs diviseurs stricts est inférieure au nombre. |
S' < N |
|
Presque parfait |
1 en moins dans la somme de leurs
diviseurs stricts. |
S' = N – 1 |
|
Parfait |
Il y a égalité. |
S' = N |
|
Quasi-parfait |
1 en plus. |
S' = N + 1 |
|
Nombre abondant |
La somme de leurs diviseurs stricts
est supérieure au nombre. |
S' > N |
|
|
||
|
Définition |
Un
nombre entier est déficient s'il est inférieur à la somme de ses diviseurs
stricts. |
|
|
Exemple |
Les
diviseurs stricts de 10 sont: 1, 2, 5 et leur somme (8) est inférieure à 10.
Le nombre 10 est déficient. |
|
|
Liste |
4, 8, 9,
10, 14, 15, 18, 21 … Il
en existe une infinité, aussi bien pairs qu'impairs. |
|
|
Propriétés |
La
déficience d'un nombre s'étend de n – 1 pour les nombres presque-parfaits à 1
pour les nombres premiers. Sont
déficients: les
puissances d'un nombre premier, y compris les puissances de 2; les
produits p . q avec p
et q premiers différents; les
diviseurs des nombres déficients ou des nombres parfaits. |
|
|
Anglais |
Deficient
or defective numbers |
|
|
Suite |
||
|
|
||
|
Définition |
Un
nombre entier est abondant s'il est inférieur à la somme de ses diviseurs
stricts. |
|
|
Exemple |
Les
diviseurs stricts de 12 sont: 1,
2, 3, 4 et 6 et leur somme ( Le
nombre 12 est abondant. C'est le plus petit nombre abondant. |
|
|
Liste |
12, 18,
20, 24, 30, 36, 40, 42, 48 … Ils
sont 21 inférieurs à 100. |
|
|
Propriétés |
Le
premier trouvé a été 45 045
= 3²·5·7·11·13, avec S' = 59 787.
|
|
|
Anglais |
An abundant number or excessive number is a number
for which the sum of its proper divisors is greater than the number itself. |
|
|
Suite |
Nombres abondants:
caractérisation et tables |
|
|
selon définition de Ramanujan |
|
|
|
Définition |
Suite
des nombres qui établissent un nouveau record en quantité
de diviseurs. |
|
|
Exemple |
1, 2, 4,
6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040 … |
|
|
Propriétés |
Infinité. Ramanujan
(1915) en a fait la liste jusqu'à 6 746 328 388 800, en oubliant 293 318 625
600. Les
facteurs sont les premiers consécutifs. Les
exposants vont à égalité ou en décroissant. L'exposant
final est toujours égal à 1. |
|
|
Anglais |
Highly composite
number. |
|
|
Suite |
||
|
|
||
|
Définition |
Un nombre n tel que, pour tout k
< n, on ait:
Ce nombre dépasse tous les
précédents en proportion d'abondance. |
|
|
Exemple |
|
|
|
Liste |
1, 2, 4,
6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1 260, 1 680, 2 520, 5
040, 10 080, 15 120, 25 200, 27 720, 55 440, 110 880, 166 320 … Il
en existe une infinité. |
|
|
Propriété |
Les
dix-neuf premiers superabondants sont aussi hautement
composés. |
|
|
Suite |
||
|
|
||
|
Définition |
Un nombre n est dit colossalement
abondant si et seulement si il existe un nombre e > 0 tel que, pour tout k
> 1:
|
|
|
Liste |
1, 2, 4, 6,
12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1 260, 1 680, 2 520, 5 040,
7 560, 10 080, 15 120, 20 160, 25 200, 27 720, 45 360, 50 400, 55 440 … |
|
|
Propriété |
Ils
sont aussi superabondants. |
|
|
|
||
|
Définition |
Nombres
égal à la somme de ses diviseurs stricts
(sigma prime). Définition alternative avec la part aliquote: celle-ci est tout simplement un
quotient exact du nombre. Par exemple les parts aliquotes de 10 sont 10/10 = 1,
10/5 = 2 et 10/2 = 5. Un nombre parfait est un nombre qui est égal à la somme
de ses parts aliquotes. |
|
|
Exemple |
|
|
|
Liste |
6,
28, 496, 8 128 … |
|
|
Propriétés |
On
ne sait toujours pas s'il existe des nombres parfaits impairs. En fait, on ne sait pratiquement rien sur
la perfection des nombres impairs! Ils sont tous de la forme 2n – 1 (2n – 1) où (2n – 1) est un nombre
de Mersenne premier. |
|
|
Anglais |
Perfect
numbers |
|
|
Suite |
||
|
|
||
|
Définition |
Soit
d un diviseur de n, il est un diviseur unitaire de n s'il est premier avec n/d.
Un
nombre unitairement parfait est égal à la somme de ses diviseurs unitaires. |
|
|
Liste |
6, 60, 90,
87 360, 1,4582… 1023 |
|
|
Propriétés |
On
ne connaît que ces cinq là. On
conjecture qu'ils sont en nombre limité. |
|
|
Anglais |
Unitary
perfect number |
|
|
Suite |
||
|
|
||
|
Définition |
Nombre
égal à la somme de certains de ses diviseurs. |
|
|
Exemple |
20 = 1 + 4
+ 5 + 10 |
|
|
Liste |
6, 12, 18,
20, 24, 28, 30, 36, 40, 42, 48, 54, 56,
60, 66, 72, 78, 80, 84, 88, 90, 96 … 100, 102 …
Suite >>> |
|
|
Propriétés |
Contraire
des nombres étranges. Tous
les nombres en 6 k sont semi-parfaits. |
|
|
Nombre pseudo parfait
primitif |
Un
pseudo-parfait dont aucun de ses diviseurs n'est lui-même pseudo-parfait: 6, 20, 28, 104, 272 … |
|
|
Anglais |
Pseudoperfect or
semiperfect numbers (prononcez "sudo pefékt") Primitive
pseudoperfect |
|
Suite détaillées en Nombres semi-parfaits
|
|
||
|
Définition |
Nombre
déficient, égal à la somme de ses diviseurs propres
à + 1 près. |
|
|
Exemple |
n
= 16, somme des diviseurs propres: 1 + 2 + 4 + 8 = 15. |
|
|
Liste |
1, 2, 4,
8, 16, 32 … |
|
|
Propriétés |
Tous
les nombres de la forme 2n sont déficients, presque
parfaits. En existe-t-il d'autres? Question ouverte. Aucun
autre presque-parfaits en 2n
+ 1, ni de presque-parfaits en 2n - 1 n'ont été trouvé, sans qu'il soit
prouvé qu'ils n'existent pas. |
|
|
Anglais |
Almost
perfect number |
|
|
Suite |
||
|
|
||
|
Définition |
Nombre
abondant, égal à la somme de ses diviseurs propres à
– 1 près. |
|
|
Exemple |
n
= 16, somme des diviseurs propres: 1 + 2 + 4 + 8 = 15. |
|
|
Propriétés |
S'il
en existe, ils sont supérieurs à 1035. Ils
seraient le carré d'un nombre impair et aurait plus de 7 diviseurs distincts. |
|
|
Anglais |
Quasiperfect
number |
|
|
|
||
|
Définition |
La
somme des diviseurs, y compris lui-même, fait trois fois le nombre. L'index du nombre vaut 3. Un
nombre k-parfait est un nombre dont l'index vaut k. |
|
|
Exemple |
|
|
|
Liste |
, 459 818
240, 1 476 304 896, 51 001 180 160 |
|
|
Propriétés |
Trouvés
en 1557 par Mersenne. On
ne connaît que six nombres triparfaits. On pense que c'est tout. |
|
|
Multi parfait k-parfait |
2-parfaits: 6, 28, 496, 8128 … 3-parfaits: 120, 672, 523 776 … 4-parfaits: 30
240, 32 760, 2 178 540, 23 569 920 … 5-parfaits: 14
182 439 040, 31 998 395 520, 518 666 803 200 … |
|
|
Anglais |
Triperfect number,
multi-perfect number, k-perfect number |
|
|
Suite |
Nombres triparfaits, nombres multiparfaits |
|
|
|
||
|
Définition |
Quantité
de diviseurs et somme des diviseurs sont deux nombres parfaits |
|
|
Exemple |
12
est un nombre sublime, car il a 6 diviseurs qui font la somme 28. |
|
|
Liste |
12, 608655 5670238378 9896703717 3424316962
2657830773 3518859705 2832486051 2791691264 |
|
|
Propriétés |
On
ne connaît que 2 nombres sublimes. |
|
|
Anglais |
Sublime number |
|
|
Suite |
||
|
Paires amiables ou amicales |
|
||
|
Définition |
Généralisation
à des couples de la notion de nombres parfaits: la somme des diviseurs de chacun
est égale à l'autre nombre |
||
|
Exemple |
220 est
divisible par: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 et 110 qui ajoutés donnent
284. Or 284 est divisible par 1, 2, 4, 71 et 142, dont la somme est 220. |
||
|
Liste |
220 1 184 2 620 5 020 12 285 17 296 1 175 265 9 437 056 … |
& 284 & 1
210 & 2
924 & 5
564 & 14
595 & 18
416 & 1
438 983 & 9
363 584 … |
|
|
Propriétés |
La
paire 12 285 / 14 595 est la première impaire. La
paire 17 296 / 18 416 est la deuxième connue. |
||
|
Anglais |
Amicable
pair |
||
|
Suite |
|||
|
Chaînes amiables ou
amicales |
|
|
|
Définition |
Généralisation
de la notion de nombres amiables. On peut prolonger la
boucle somme
des diviseurs, nouveau nombre, somme
de ses diviseurs, etc. et
tenter de retrouver le nombre initial après n étapes. Si
c'est le cas, le nombre de départ est dit " sociable d'ordre n ". |
|
|
Liste |
12 496, 14
288, 15 472, 14 536, 14 264 … |
|
|
Propriétés |
Deux
premiers découverts par P. Poulet, mathématicien français, en 1918. Ordre
5: 12 496 / 14 288 / ... Ordre
28: 14316 / ... En
1969, Henri Cohen, Paris, en découvre 7 d'ordre 4. |
|
|
Anglais |
Sociable
numbers |
|
|
Suite |
||
|
|
||
|
Définition |
Un
nombre abondant pour lequel il est impossible de trouver une somme de
certains de ses diviseurs, égale à lui-même. |
|
|
Exemple |
Diviseurs
de 70
= {1, 2, 5, 7, 10, 14, 35} Somme 74 Aucune
somme partielle n'est égale à 70. |
|
|
Liste |
70, 836,
4 030, 5 830, 7 192, 7 912, 9 272, 10430, 10570, 10792, 10990, 11410,
11690, 12110, 12530, 12670, 13370, 13510, 13790, 13930, 14770, 15610, 15890,
16030, 16310, 16730, 16870, 17272, 17570, 17990, 18410, 18830, 18970, 19390,
19670, … OEIS A006037 |
|
|
Propriétés |
On
ignore s'il existe un nombre
étrange impair. Les
nombres de la forme n = 2k pq , avec p et q premier, sont étranges
pour une large majorité d'entre d'eux. Ce qui laisserait penser que les
nombres étranges primitifs seraient en nombre infini. Giuseppe
Melfi Contraire
des nombres semi-parfaits. Voir nombres pseudo-parfaits |
|
Anglais Weird numbers
|
|
||
|
Définition |
Nombre
qui n'est jamais la somme des diviseurs propres d'un autre nombre. Jamais antécédent
aliquote. |
|
|
Liste |
2, 5, 52,
88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262, 268, 276, 288,
290, 292, 304, 306, 322, 324, 326, 336, 342, 372, 406, 408, 426, 430, 448,
472, 474, 498, 516, 518, 520, 530, 540, 552, 556, 562, 576, 584, 612, 624,
626, 628, 658 … |
|
|
Propriétés |
Infinité
– Prouvé par Erdös. Conjecture
non démontrée: 5 est le seul intouchable impair. |
|
|
Anglais |
Untouchable number:
not the sum of the proper divisors of any number |
|
Voir Auto-nombres
Intouchables
|
Film d'Olivier
Nakache et d'Éric Toledano (2011). Avec
Omar Sy, François Cluzet, Audrey Fleurot … Avec 19,44 millions d'entrées (2012)
c'est le deuxième plus gros succès français dans l'histoire de son box
office, derrière Bienvenue chez les Ch'tis. Le film est devenu en 2012 le
film français le plus vu hors de France détrônant ainsi Le Fabuleux Destin
d'Amélie Poulain qui détenait le titre depuis près de dix ans. Source Wikipédia. |
|
|
||
|
Définition |
Nombres
dont la somme des diviseurs est un carré. |
|
|
Exemple |
66 =>
1 + 2 + 3 + 6 + 11 + 22 + 33 + 66 = 144 = 12² |
|
|
Liste |
3, 22, 66, 70, 81 |
|
|
Suite |
||
|
|
||
|
Définition |
On
compte la quantité de chiffres pour écrire les facteurs. On
compare à la quantité de chiffres du nombre lui-même.
|
|
|
Suite |
||
|
|
||
|
Définition |
Nombre
dont la somme des chiffres est égale à la somme de tous les chiffres de ses
facteurs premiers. |
|
|
Exemple |
4 = 2 x
2 Somme chiffres = 4 22
= 2 x 11 Somme chiffres = 4 27
= 3 x 3 x 3 Somme chiffres = 9 666 = 2 x 3 x 3x 37 Somme chiffres = 18 |
|
|
Liste |
4, 22, 27,
58, 94, 121, 166, 202, 265 … |
|
|
Propriété |
Ils
sont 376 jusqu'à 10 000. Les
nombres premiers sont exclus car trivial. Nombre
k-smith: somme des chiffres = k fois sommes des chiffres des facteurs. Ex: 32
est 2-smith car 3+2 = 5 et 2+2+2+2+2 = 10. |
|
|
Suite |
Nombre de Smith / Nombre -motif de Smith / Grand
nombre de Smith |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Diviseur.htm
|
![]()