NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/10/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Algèbre
Débutants Équations	ÉQUATIONS			Glossaire Équations 2^e degré
INDEX Équations Algèbre	Généralités	Techniques de base	Diophantienne
	Premier degré	Deuxième degré	Troisième degré
	Deux inconnues	Deux équations ou plus	Déterminant
	Inéquation	Avec exposant
		Sommaire de cette page >>> Tour d'horizon >>> Historique >>> Théorème d'Abel ou d'Abel-Ruffini >>> Écriture

Équation fallacieuse, mais astucieuse !

Voir Pensées et Humour

ÉQUATIONS

La recherche de leurs solutions a marqué plusieurs étapes dans la vie des nombres. On a cherché des nombres entiers, réels puis imaginaires (complexes), etc.

Houp! Tout cela m'a toujours parut très compliqué!

Alors, allez voir les sujets suivants:

Initiation aux quatre opérations

SOS – Équations débutant

Techniques de base de l'algèbre

TOUR D'HORIZON – Une inconnue
>>>	1^ER DEGRÉ ax + b = 0	Solution simple.
>>>	QUADRATIQUE ax² + bx + c = 0	Connue depuis les Babyloniens en 1600 av. J.-C. Voir Puzzle du fermier
>>>	CUBIQUE ax^3+ bx²+...	Résolu à la Renaissance par Scipio del Ferro et Niccolo Fontana dit Tartaglia et publié par Girolamo Cordano en 1545. Voir Nombre 2,094
	QUARTIQUE ax^4+ bx^3+...	Résolu par Ludovico Ferrari et publié par Cordano son maître dans le même ouvrage que ci-dessus. La formule est particulièrement compliquée. Voir Résolution par tableur / Problème du billard d'Alhazen
	QUINTIQUE ax^5+ bx^4+ ...	Pas de solution analytique. En 1770, Joseph-Louis Lagrange montre que pour résoudre les équations quadratiques, cubiques et quartiques, on utilise le même artifice. Il ne marche pas pour le cinquième degré. Mais existe-t-il un truc semblable utilisant les arrangements et permutations. Personne ne trouva. En 1824, Niels Hendrick Abel (20 ans), puis Évariste Galois, en 1831 (20 ans), prouvent séparément qu'aucune formule n'existe. Plus précisément >>> Voir Naissance de l'algèbre moderne / Résolution d'un cas particulier / Symétries et solvabilité des équations / Hermite

TOUR D'HORIZON – Deux inconnues
>>>	ax + by + c = 0	Si le  le PGCD de a et b divise le nombre c, l'équation possède une infinité de solutions.
>>>	ax + by + c = 0 a'x + b'y + c' = 0	Résolution des systèmes d'équations. Ce qui nécessite autant d'équations distinctes que d'inconnues.

TOUR D'HORIZON – Autres: Diophantienne, Pell …
>>>	Autres formes & Types de résolution	Voir le lien indiqué qui conduit à Équation – Glossaire et index
>>>	Avec inconnue en exposant	Nécessité de recourir aux logarithmes.

Voir Équations avec des radicaux

HISTORIQUE
Sumériens La méthode de résolution des équations du second degré était déjà connue des Sumériens, aux environs de 2000 av. J.-C. et Babyloniens vers 1700 av. J.-C. Au XVI^e siècle Les mathématiciens italiens Niccolò Tartaglia (1499-1557) et Jérôme Cardan (1501-1576) découvrirent des formules similaires, en utilisant des racines carrées et des racines cubiques, pour résoudre des équations du troisième et du quatrième degré (équations qui font intervenir les puissances trois et quatre de l'inconnue). Ludovico Ferrari (1522-1565), élève de Cardan, aura raison du quatrième degré en 1540. Par la suite Les mathématiciens cherchèrent sans succès durant plusieurs siècles des formules analogues pour les équations du cinquième degré. Pour sa thèse, Gauss démontre le théorème fondamental de l’algèbre donnant la quantité de solutions possibles des équations algébriques. Au début du XIXe siècle Les mathématiciens Paolo Ruffini, Niels Henrik Abel (1802-1829) et Évariste Galois (1811-1832) démontrèrent que ces formules n'existaient pas. Leurs travaux donnèrent naissance à une branche importante de l'algèbre moderne : la théorie des groupes, qui étudie la symétrie d'une manière générale, et en particulier celle des racines des polynômes. Voir Groupes Historique
1^er degré Linéaire Fonction affine	2^e (second) Quadratique	3^e Cubique	4^e Quartique	5^e et + Quintique

Aide logicielle à la résolution des équations

Les logiciels mathématiques (Maple, Mathematica, …) et les calculateurs d'équations sur Internet (équation calculator2) sont capables de résoudre de nombreuses équations.

L'intelligence artificielle prend le relais pour les cas compliqués. En 2020, une IA a réussi à résoudre 99,7% des 100 millions d'équations proposées quand un logiciel classique avait réussi à 84%.

Théorème d'Abel ou d'Abel-Ruffini

On s'intéresse aux polynômes P(x) de degré n et à l'équation P(x) = 0. L'équation du 5^e degré n'a pas de solution analytique. Il existe des polynômes de degré supérieur ou égal à cinq et à coefficients complexes dont les racines ne s'expriment pas par radicaux. Le groupe symétrique Sn n'est pas solvable pour n > 4. Théorème de d'Alembert-Gauss: une équation de degré cinq à coefficients complexes admet toujours au moins une solution, mais la racine ne s'exprime pas toujours par radical. Plus généralement, ce théorème indique qu'une équation à coefficients entiers, rationnels, réels ou complexes admet au moins une racine complexe. Il n'est pas toujours possible d'exprimer cette racine à partir des coefficients du polynôme, de la valeur 1, des quatre opérations, et de l'extraction des racines nièmes (radicaux). Il existe de méthodes numériques qui permettent la recherche des racines quel que soit le degré du polynôme, comme la méthode de Newton. Méthodes numériques, car les calculs sont réalisés sur de nombres. La formulation littérale (algébrique, avec des lettres …) n'est possible, systématiquement, que pour le polynôme de petit degré: 2, 3 et 4. La formule fait intervenir des racines comme dans le cas du deuxième degré. Historique 1799 – Paolo Ruffini montre qu'il n'y a pas de solution pour une équation quintique. 1824 – Niels Henrik Abel l'a démontré en utilisant un raisonnement par l'absurde. 1831 – Évariste Galois donnera une condition nécessaire et suffisante d'expression des racines sous forme de radicaux. Il montre que ce n'est pas le degré d'une équation qui mesure la difficulté de la résoudre mais c'est la nature de son groupe. Abel démontre qu'il n'existe pas de formule permettant la résolution systématique des équations quintiques. Il essaie de caractériser les solutions lorsqu'elles existent. Mort trop tôt, c'est Galois qui va s'attaquer à cette tâche. Il aura l'idée de traiter le problème via les symétries des solutions des équations. Jusqu'au degré quatre, les symétries sont "sages", régulières; par contre, à partir de cinq, "ça dérape!".

ÉCRITURE des équations
Exemple de problème	Traduction en équation
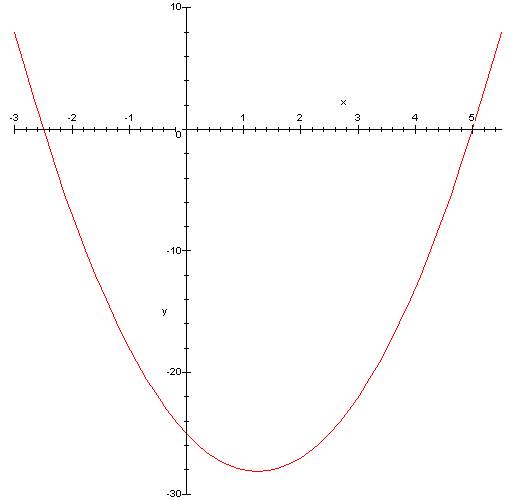
Énoncé Trouvez le nombre tel que le double de son carré diminué de cinq fois lui-même donne vingt-cinq Solutions -2,5 et 5	Moderne	2 x² – 5 x = 25
	Nicolas Chuquet 1470	2^2 m 5^1 égault a 25
	Cardan 1545	duo quad.m qumque reb. aequalis 25
	Stiffel 1525	2z aequatus 5x + 25
	Pierre de la Ramée 1586	2q – 5l aequatus sit 25
	Harriot 1631	2au – 5a = 25
	Descartes 1637	2zz – 5z ¥ 25

D'après Encyclopédie des jeunes - Larousse

Graphique de cette équation (ci-dessus)
Les racines (– 2,5 et 5) se trouvent à l'intersection de l'axe des x avec la courbe.

Suite	Équation – Glossaire et index Techniques de base Exercices simples Équations énigmatiques – Index Voir haut de page
Voir	Algorithme d'Héron Équation avec racines carrés Équation de Pell Équation en x^4 par factorisation Équations diophantiennes Inéquations Les 17 équations qui ont changé le monde Méthode de Newton Puissance quatrième Structure algébriques et équations
Cette page	http://villemin.gerard.free.fr/ThNbDemo/EqaGene.htm